基于灰色傅里叶残差修正的上证指数30日均价预测

史丽萍，闫海波

（新疆财经大学 数学学院，新疆 乌鲁木齐 830012）

上证指数（SH000001）的全称是上海证券交易所股票价格综合指数，是由上海证券交易所编制的股票指数，1990年12月19日正式开始发布。该股票指数是一种股价加权平均指数，权数为上市公司的总股本，由于我国上市公司的股票有流通股和非流通股之分，其流通量与总股本并不一致，所以总股本较大的股票对股票指数的影响就较大。上证指数的发布几乎是和股市行情的变化相同步的，可以科学的反应整个股票市场的行情，如股票整体涨跌或股票价格走势等，它是我国股民和证券从业人员判断股票价格变化趋势必不可少的参考依据，因此研究上证指数具有重要的意义。

王真真等通过考察在5%的显著性水平下，均值方程拟合的残差平方序列的不相关性的前提下建立ARCH(autoregressive conditional heteroskedasticity)模型，基于序列的自相关性比较显著，从而构造ARCH-M模型，研究发现，上证指数日收盘价的期望值与时变波动性呈现出较强的正相关性，说明上证指数常出现大起大落的现象[1]。李妍应用ARCH模型对上证指数的日收盘价进行异方差检验，发现上海证券市场具有显著的GARCH(generalized autoregressive conditional heteroskedasticity)效应和非对称情况，研究表明GARCH-M模型不适合模拟上证指数的波动性[2]。基于GARCH模型要求的参数较少，在估计或预测金融时间序列数据的波动性和相关性方面的效果比较显著，雒佳文利用GARCH（1,1）模型对上证指数日收盘指数拟合，构建ARCH和GARCH项的关系式，得出整个时间序列的变化规律，本期的条件方差在很大程度上决定上证指数日收盘指数市场的下一期条件方差[3]。

为了更加有效的预测出未来股价，雒佳文利用HP滤波分离上证指数收盘价的趋势和波动，用指数平滑法预测未来5个月的上证指数价格的变动趋势，虽然该方法规避了波动成的影响，但突发事件或其他风险的冲击会改变趋势，甚至可能逆转趋势，仅仅以趋势线判断未来的走势是有失偏颇的[4]。基于灰色预测模型所需要的数据量比较少，预测比较准确，精度较高，样本分布不需要有规律性，计算简便，检验方便等特点，栾珺采用灰色GM(1，1)模型预测上证指数，在同一等高线范围内的预测趋势和实际趋势大致相同，说明该模型具有一定的可行性[5]。由于股票的时间序列数据具有较强波动性[1]和噪声，传统的灰色模型GM(1，1)并不能很好的降低时间序列的波动性，减弱噪声对上证指数的影响，预测效果不理想。

国外学者对股票价格的预测也做一定的研究，Lee等运用支持向量机和神经网络预测股市的走势[6-7]，而Rollner则用机器学习对股市进行预测做了详细的综述[8]。运用反向传播神经网络模型预测上证综指的日变化特征。Bing等在模型中构造了学习算法和梯度搜索技术[9]，该神经网络模型成功地应用于上证指数日最高、最低、收盘价预测，但短期内无法预测上证综指的收益率。

文章在灰色模型GM(1，1)[10]的基础上，首先选取14个上证指数的30日均价，对其进行灰色预测，得到30日均价的首次预测值、残差和相对平均误差值，为了进一步降低股价的波动性，再对残差进行灰色预测[11]，得到新的预测残差；为了减弱噪声对股价的影响，采用傅里叶变换修正残差[12-16]，即从新的残差序列中选取前10个数据对其进行傅里叶变换，得到最终的预测模型；最后求出上证指数预测值的相对平均误差为0.037 3%，比传统的灰色模型GM(1，1)的平均相对误差降低了0.05%。

1 模型建立

灰色预测通过对上证指数的30日均价序列进行累加生成可以弱化随机性、指数规律性较强的曲线。由于上证指数的股价受到各种因素的影响，因此，传统的灰色GM(1，1)模型在预测应用方面有很大的局限性，为了改进灰色GM(1，1)建模机理本身的缺陷，文章通过对由灰色GM(1，1)模型预测上证指数30日均价产生的残差进行灰色GM(1，1)建模，以提高预测的精度。

1.1 残差灰色预测GM(1，1)模型[11]

设灰色方程为

则该方程解为

记u=(a,b)T为参数列，

则上证指数30日均价的预测序列为：

上述序列的残差等于原始数值与预测数值之差，即

因此，该残差序列为：

1.2 傅里叶残差修正模型[18]

由于股票价格受各种制度、股票价值和供求力量等众多因素的影响，在不同时期会以不同的指数率变化，而傅里叶级数是周期函数，可提炼出数据样本序列中隐含的周期信息，起到降噪作用[14]，通过结合灰色GM（1,1）模型，可以有效的发现时间序列中存在的不同指数信息，并提高灰色GM（1,1）模型预测的精度。

上证指数30日均价的傅里叶残差修正模型的具体步骤如下：

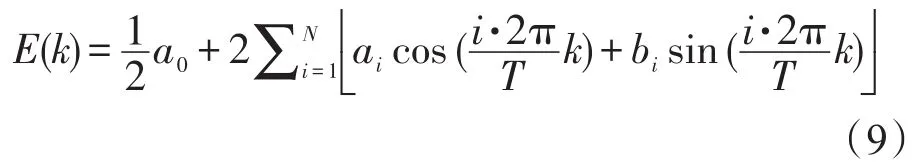
其中

1.3 预测效果检验

1.3.1 相对误差

相对误差φ(k)是绝对误差与真实值的比值，即上证指数30日均价的预测值与实际值的差值，也就是文章中的残差1序列，用该序列除以原始序列就得到了相对误差序列，即

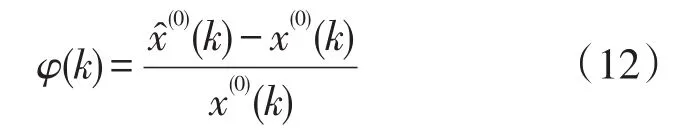
1.3.2 平均相对误差

如果计算出的相对误差和平均相对误差越小，则说明灰色傅里叶残差修正模型的预测效果越好。

2 实证分析

2.1 上证指数30日均价灰色GM(1，1)预测

文章采用的数据是2016年12月1日—2016年12月30日上证A股大盘指数的30日均价，数据来自同花顺，如表1所示。

对这14个上证指数30日均价建立灰色预测模型GM（1,1），得到其预测函数

通过预测函数可以得到其预测值，表2所示，然后再利用公式（4）得出上证指数30日均价的残差，如表2所示，可知灰色模型预测的相对平均误差为0.086 3%。

表1 中国2016/12/1-2016/12/20上证指数的30日均价

2.2 灰色傅里叶残差修正模型预测

首先，对表2中的残差1建立灰色预测模型GM(1,1)，得到残差1的预测函数：

相应的预测值和残差2，如表3所示。

其次，对表3中前10个残差2建立傅里叶修正残差模型，得到残差2的傅里叶修正函数：

2.3 预测2016年12月19和20日的30日均价

由于灰色GM（1,1）模型每次在预测原始序列的过程中都会缺失一个数据。因此，在后续的预测过程中，为保证数据的完整性，将依次补入一个数据。然后用最小二乘法求得：

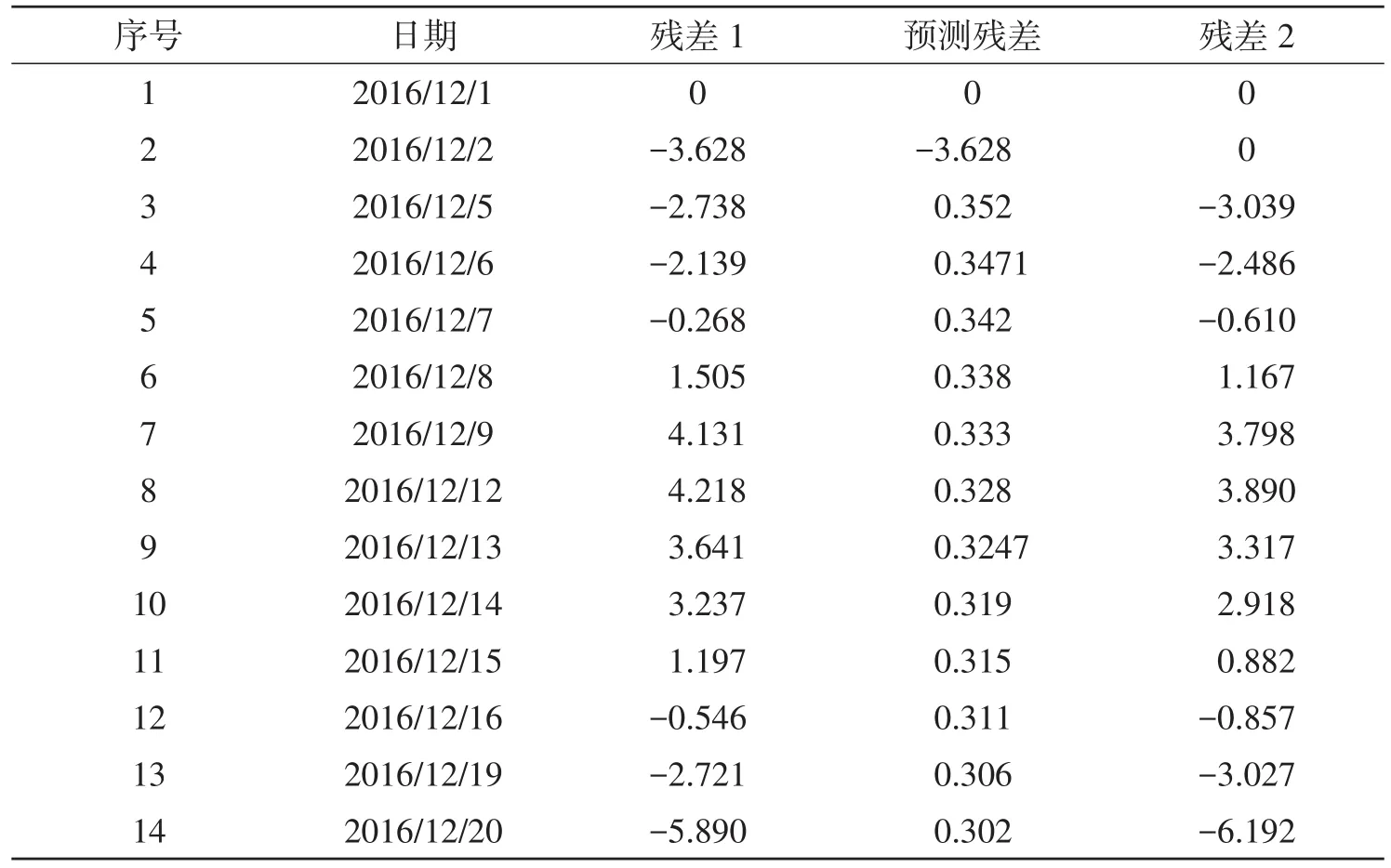
表3 灰色预测和傅里叶修正后的残差预测结果

2016年12月19日的上证指数30日均价也就是表1中的第13个数据，利用公式（7）可以计算得到，具体算法如下：

同理也可以预测出2016年12月20日的上证指数30日均价，即

以此类推可以预测出上证指数未来的30日均价。

3 预测效果检验

首先，利用公式（12）可以计算出2016年12月19日和12月20日的日均价相对误差，如表4所示。

其次，利用公式（13）可以计算其平均相对误差，即

通过模型检验得出经过傅里叶修正的残差灰色模型预测的平均相对误差为0.037 3%，而传统灰色模型预测值的相对平均误差为0.086 3%，说明灰色傅里叶残差修正模型的预测精度比传统的灰色模型有所提高。

4 小结

上证指数能够直接反映股市行情的变化情况，因此文章构建上证指数30日均价的灰色傅里叶级数残差修正模型，对30日均价进行预测，通过预测效果检验计算出平均相对误差为0.0373%；而传统的灰色GM（1,1）预测的平均相对误差为0.0588%，通过对比可以发现，灰色傅里叶级数残差修正模型的预测精度比灰色GM（1,1）模型的预测精度高，相对平均误差降低了0.05%,由此可以说明该模型在股价的预测方面有一定的实用性。

表4 灰色傅里叶残差修正模型的预测值