分布式在线随机投影优化

王俊雅

（安徽理工大学 数学与大数据学院，安徽 淮南 232001）

分布式网络由个体间相互交换信息耦合而成，个体仅与邻居节点进行通信使个体状态趋于一致[1-2]，由于不需要全局信息，它在复杂网络环境下具有极强适应性。近年来，随着计算机通信技术的进一步发展，分布式优化在大型计算和海量数据处理、机器学习等多方面有着广泛应用[3-5]。

实际上，分布式网络运行在动态变化和不确定的环境中，对复杂网络成本函数造成重大影响，难以建立优化模型。文献[6]提出了基于Pushsum的分布式对偶平均算法，解决优化问题。但并不能实时处理网络数据流，造成网络中时间和资源浪费。为了解决这一问题，将网络资源和分布式数据流结合在一起，本文考虑在线优化算法，分布式在线优化算法不仅有效提高了算法的鲁棒性，且在深度学习和网络数据流处理方面有着重要应用[7-8]。文献[9]提出了分布式在线交替方向乘子法，可以对网络采集的数据进行实时处理和分析，并在理论上分析了其学习性能。作为衡量在线优化算法性能的一个重要指标，Regret界刻画了随时间推移的累积成本与最佳固定决策所产生的成本之间的差值，因此在线优化算法的优劣可由Regret界的大小进行判断[10-11]。

文献[12]提出了分布式随机投影算法，不仅能够处理大规模网络数据，而且能消除局部目标函数差异性，但占用内存空间大，成本代价高昂。本文将分布式随机投影优化算法扩展到在线设置，运用在线分布式优化框架，提出了分布式在线随机投影(distributed online random projection,DORP)优化算法，解决了对分布式网络采集的数据流进行实时分析处理的问题，减少了资源浪费，降低了成本代价和时间消耗。

1 相关图论知识

引入有向图G=(V,Et,At)描述t时刻节点之间的相互作用，其中V={1,2,…,n}表示节点集，E表示交互链路集，A表示权重矩阵。有向边(i,j)∈E表示节点i可以直接从节点j接收信息。每个节点都包含在其外邻和内邻表示为：

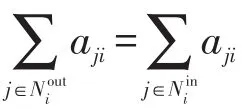
2 分布式在线约束优化

考虑n个节点的凸优化问题：

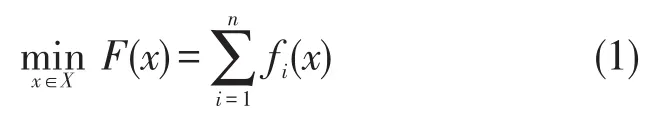
s.t.gi(x)≤0,j=1,2,…,n。

其中X∈Rm表示所有节点的凸集，fi:Rm→R表示仅由节点i已知的凸函数，节点i仅知道它的局部约束gi(x)≤0，其中是凸函数的向量。

为了衡量分布式在线学习优化算法，对∀t=0,1,…T本文定义了分布式在线Regret界：

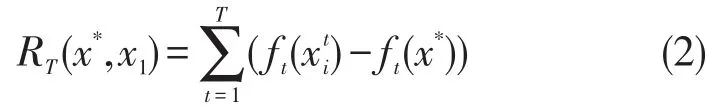
建模一个轮次递归算法来解决非平衡有向图上带有时延的分布式在线问题(2)，即每个节点i都与邻居交流，并在本地更新一个向量，对应给出，最终使每个达到一致收敛。

3 分布式在线投影算法(DORP)

算法1 分布式在线投影算法(DORP)

4 收敛性分析

为了证明算法1的收敛性，将问题转化为以下形式：

引理1(指数增长稳定性)向量序列由下式生成：

引理2(随机稳定性)Ft是由随机变量取决于时刻t生成的σ域，由假设知：

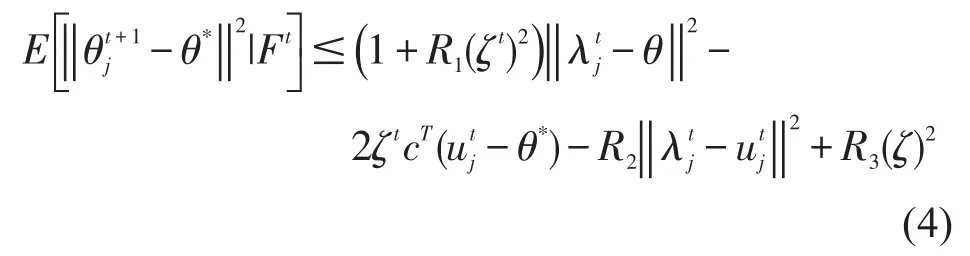
其中R1,R2,R3是正常量。

引理3(上鞅收敛)和是非负随机变量序列，则

定理1序列一致收敛到集合Θ*中最优值，即，则当。

证明因为凸性和At是行随机的，即，得到：。

5 数据实验

图1 损失性能

6 小结

本文将分布式随机投影算法扩展到在线设置，提出了DORP算法，该算法不仅能够处理大规模网络数据，消除局部目标函数差异性，而且能及时处理网络中的数据流，减少了储存空间和成本代价。未来考虑DORP算法扩展到异步或者应用于解决链路故障问题。