带有扰动的非线性系统的自适应模糊控制*

李彦欣

(山东科技大学 数学与系统科学学院,青岛 266590)

模糊控制一直被认为是解决复杂非线性系统建模和控制问题的一种行之有效的方法．基于不同的模糊模型研究非线性系统的稳定性与控制器设计一直是模糊控制领域所关注的问题之一．特别地，由于模糊系统具有万能逼近特性，不确定非线性系统的自适应模糊控制已经成为自动控制领域近年来一个活跃的研究方向.自适应模糊Backstepping 控制方法的主要优点在于能够有效地处理一类严格反馈非线性未知系统的控制问题.在已有的研究中,不确定非线性系统中的函数均是含有已知参数的或者是已知的非线性函数[1-4],因此，若系统中含有未知函数，那么之前的方法是不可行的.通过自适应神经网络控制[5-7],这个问题得到了有效地解决.

神经网络或模糊逻辑系统通过对未知非线性函数的逼近特性和Backstepping技术来构造控制器.该自适应控制器保证闭环系统中所有信号的一致最终有界.然而,随着神经网络节点或模糊规则的增加,估计参数的数目将显著增加,使得计算量随之增大.为了解决这个问题,将模糊逻辑系统中理想加权向量的范数作为估计参数[8-12],而不是加权向量的元素.因此,自适应律的数量大大减少.

与现有的所有的自适应模糊控制不同,Mamdani型模糊系统是用来直接逼近所需的输入信号,而不是系统中未知的非线性函数.针对这一问题,本文将提出一种新的自适应模糊控制方法,该方法的主要优点是,对于一个n阶严格反馈非线性系统,通过其逼近特性和Backstepping技术设计了自适应模糊控制器,使得只有一个参数需要计算.因此,计算负担显著降低,在实践中很容易实现.

1 问题的描述及预备知识

1.1 问题的描述

考虑以下一类非线性系统

(1)

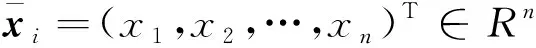
本文对于系统(1)设计一个自适应模糊控制器,使得在一定概率下，闭环系统中所有的信号半全局一致连续有界,并且跟踪误差收敛到原点的一个充分小邻域内．

1.2 预备知识

假设1 跟踪目标yd(t)和他的n阶导数是连续有界的.

引理1 对于 ∀(x,y)∈R2,有不等式(2)成立[13]

(2)

其中ε>0,p>1,q>1,且 (p-1)(q-1)=1．

在控制器的设计和稳定性分析中,采用模糊逻辑系统来逼近一个定义在紧集上的未知连续函数．因此，模糊系统的模糊规则为：

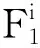
则y是Gi,i=1,2,…,N.

若采用单点模糊化、乘积推理和中心加权模糊化方法，则模糊系统的输出可表示为

(3)

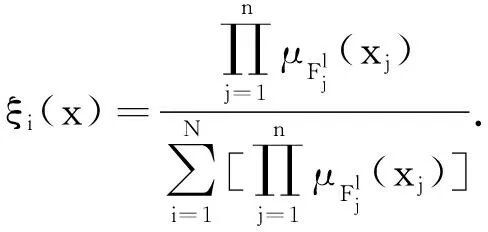
其中ξ(x)=[ξ1(x),ξ2(x),…,ξN(x)]T．模糊逻辑系统(2)变为

y=ΦTξ(x)

(4)

引理2 如果f(x) 是定义在一个紧集Ω上的连续函数,那么对 ∀ε>0,存在一个模糊逻辑系统(式(3))满足[14]

(5)

2 主要结论

对于系统(1)通过Backstepping技术,提出自适应模糊控制方法.在每一步中通过合适的Lyapunov函数Vi,设计出一个虚拟控制函数αi,最终设计出控制律u.

Backstepping法的设计过程包含n个步骤，对于系统(1)要设计的Backstepping过程，定义一个常数为

θi=‖φi‖2,i=1,2,…,n

(6)

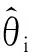
设计控制律为

(7)

其中an,ξn和λn均为正整数.

定义自适应律为

(8)

其中ri,ai,ξi和βi均为正整数.

以下陈述一个主要结果：

证明对于1≤i≤n-1,定义了虚拟控制函数αi:

(9)

其中ai,ξi和λi均为正整数.

第1步.定义坐标变换

z1=x1-yd,z2=x2-α1.

选择一个Lyapunov函数

(10)

给定V1的导数为

(11)

(12)

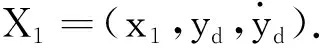
由杨氏不等式,得

(13)

其中a1为正整数.

构造一个虚拟控制函数

(14)

其中a1和λ1为正整数.

将式(13)和式(14)代入式(11),得

(15)

第2步.令z3=x3-α2,选择Lyapunov函数

(16)

给定V2的导数为

(17)

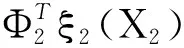
(18)

由杨氏不等式,得

(19)

其中a2为正整数.

构造一个虚拟控制函数

(20)

其中a2和λ2为正整数.

将式(15)、式(19)和式(20)代入式(17),得

(21)

第i步(3≤i≤n-1).令zi+1=xi+1-αi,假定已经完成了前i-1步,即

(22)

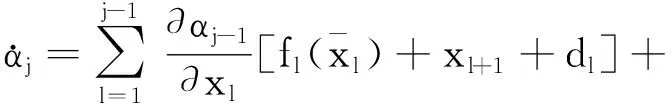
选择Lyapunov 函数

(23)

给定Vi的导数为

(24)

(25)

由杨氏不等式,得

(26)

其中ai为正整数.

构造一个虚拟控制函数

(27)

其中a2和λ2为正整数.

与式(21)类似,得

(28)

第n步.反复使用以上归纳论证,选择以下Lyapunov函数、虚拟控制器和状态反馈控制器

(29)

(30)

(31)

Vn的导数为

(32)

将式(7)代入式(31)，得

(33)

显然,

(34)

(35)

由式(33)、式(34)和式(35),得

(36)

令a0=min{2cj,βj∶1≤j≤n},

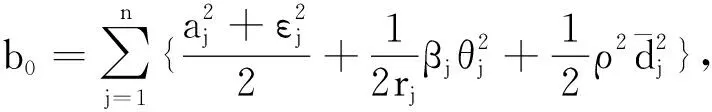
(37)

由比较原理，得

(38)

式(38)表明闭环系统中的所有信号均为有界的,特别地,有

(39)

证毕.

3 结 论

本文研究了一类不确定单输入单输出非线性严格反馈系统，提出了一种的自适应模糊控制方案，同时考虑了未知的随机扰动，通过模糊逻辑系统的逼近性和Backstepping技术构造的自适应模糊跟踪控制器解决了未知因素引起的主要难题，并证明了该方案保证了所有闭环信号在概率上均有界，而跟踪误差最终收敛到平均四值意义上原点的一个小邻域。