突出学生主体 追求自然引导*——对一道试题的讲评与反思

●

(东台市教师发展中心，江苏 东台 224200)

思维能力的提升离不开题目的练习与评讲.试题讲评对于帮助学生熟化知识、拓宽思路、积累解题经验、加深本质理解都具有十分重要的作用.当前解题教学中普遍存在教师“不顾学生学情就题论题”“只讲怎样解题却不分析为何这样解题”“只重视讲解解题过程，却不注重总结方法规律、提炼数学思想”等倾向.如何在解题教学中彰显学生的主体地位，充分暴露真实的思维过程？教师必须通过寻找和发现学生的思维“愚钝”，进行自然引导，点在关键处，引在急需处，让学生思维的火花亮起来.笔者现结合一道期末试题的讲评过程，谈谈解题教学的一些思考和感悟，与大家交流.

1 试题呈现

题目已知在四边形ABCD中，E,F分别是边AB,AD上的点，DE与CF交于点G.

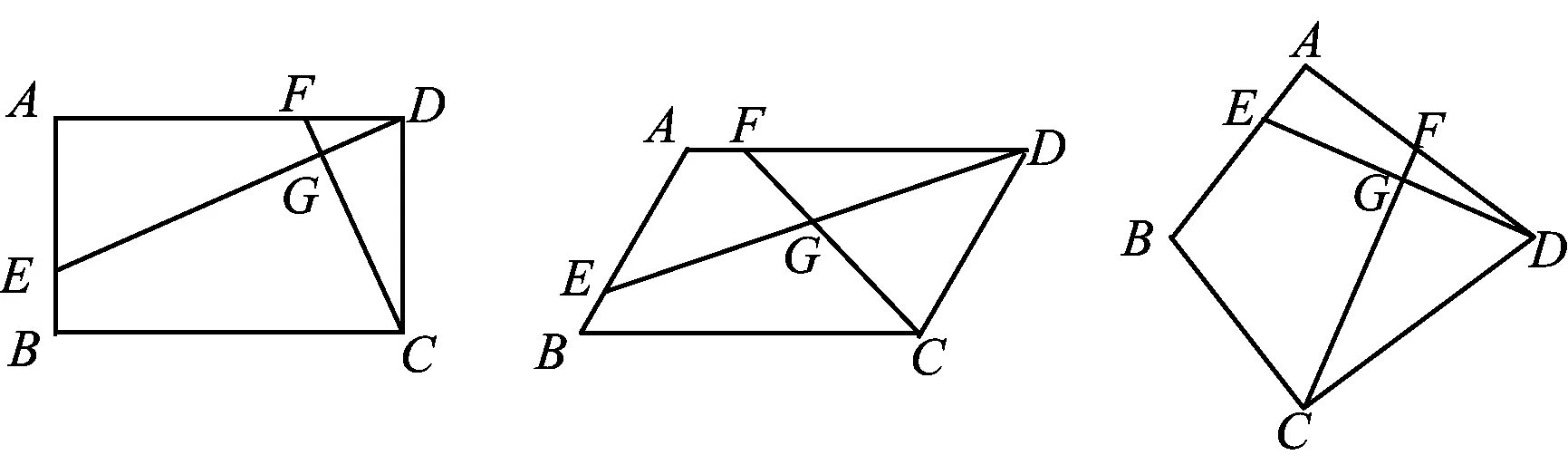
图1 图2 图3

(2013年湖北省武汉市数学中考试题第24题改编)

2 教学片断

片断1矩形中线段比的探究.

师：看第1)小题，哪位同学来谈谈自己的想法?

生1(证法1)：直接证明△ADE∽△DCF.

师(追问)：请具体说说你是怎么想的？

师：很好！要证比例式，最直接的方法就是证明线段所在的两个三角形相似，将原问题转化为证明三角形中的线段比.

图4

师：如果将第1)小题中的矩形特殊为一个正方形，其他条件不变(如图4)，则DE和CF之间的数量关系如何？

生2：相等，由△ADE≌△DCF可得.

师：本题有没有其他解法？

生2(证法2)：我是通过“中间比”进行转化的.本题中不仅有△ADE∽△DCF，而且可证△DGF与这两个三角形也分别相似.由△ADE∽△GDF,可得

(1)

由△GDF∽△DCF,可得

(2)

师：很好！通过“中间比”进行转化也是证明线段成比例的一种重要方法.还有其他方法吗?比如用三角函数的相关知识.

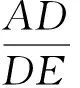
师：在直角三角形中,借助于三角函数进行线段比的转化有时会更简洁.

教学说明本题是由2013年湖北省武汉市数学中考试题第24题改编而成，第1)小题以矩形为载体着重考查了相似三角形的判定和性质.此题解法较为多样，既可以直接证明相关的两个直角三角形相似，也可以证明两个三角形都与第三个三角形相似，再通过“中间比”进行转化，还可以通过三角函数来解决问题.讲题时教师注重了基于学生的主体参与，尊重学生的真实想法，给足时间和机会让学生进行有条理的思考和表达，在此基础上教师进行精讲点拨，帮助学生总结提炼，助力思维提升.其中，通过将矩形“特殊化”——原有两个三角形的关系由相似变为全等，让学生感悟“一般”与“特殊”的关系，自然加深了对知识的认识和理解.

片断2平行四边形中线段比的探究.

师：看第2)小题，将矩形弱化成一般的平行四边形后，原有的思路、方法是否还可行？

(学生独立思考，小组讨论.)

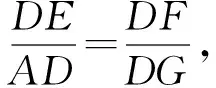
师：怎么办？现在你有完整的思路吗？

生4：还没有，我在想是不是可以通过构造三角形相似来解决问题.

师：很好！尽管你没能说出完整思路，但仍然要为你点赞，敢于表达自己真实的想法.

师：现在我们先不急于构造，看看有没有同学能够帮他把刚才这条路走通？

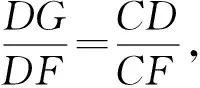
师：接着来看用“构造法”怎么做？

生6：在图1中，由于四边形ABCD为矩形，因此

∠DAE=∠CDF=90°，

从而△ADE∽△GDF，△ADE∽△DCF，将矩形ABCD改为一般的平行四边形后，∠DAE和∠CDF的相等关系发生了改变，但互补关系仍然存在，于是我想抓住互补关系进行突破.如图5，在AD的延长线上取点M，使CM=CF，则

∠CDM=∠DAE， ∠M=∠CFD=∠DEA，

这样就构造出了△DCM，且△DCM∽△ADE，剩下的就是通过证明相似来解决问题.

师：很好！生6能抓住题中的关键条件通过“构造法”来转化问题.还有其他的方法吗？

图5 图6

生7：刚才生6用的是“延长法”，我想用“截取法”.如图6，在AD上取点N，使CN=CD，容易证明∠CNF=∠DAE，以下只需证明△ADE∽△NCF即可.

师：生7的方法也很好！他与生6的方法本质上是一致的，只是构造出的三角形位置不同而已.

师：刚才我们是在边AD所在的直线上进行构造，如果在边BA所在的直线上进行构造，行不行？

(学生积极探究中,不一会有人上台讲题.)

生8：如图7，在BA的延长线上取点P，使DP=DE，只需证明△ADP∽DCF即可.

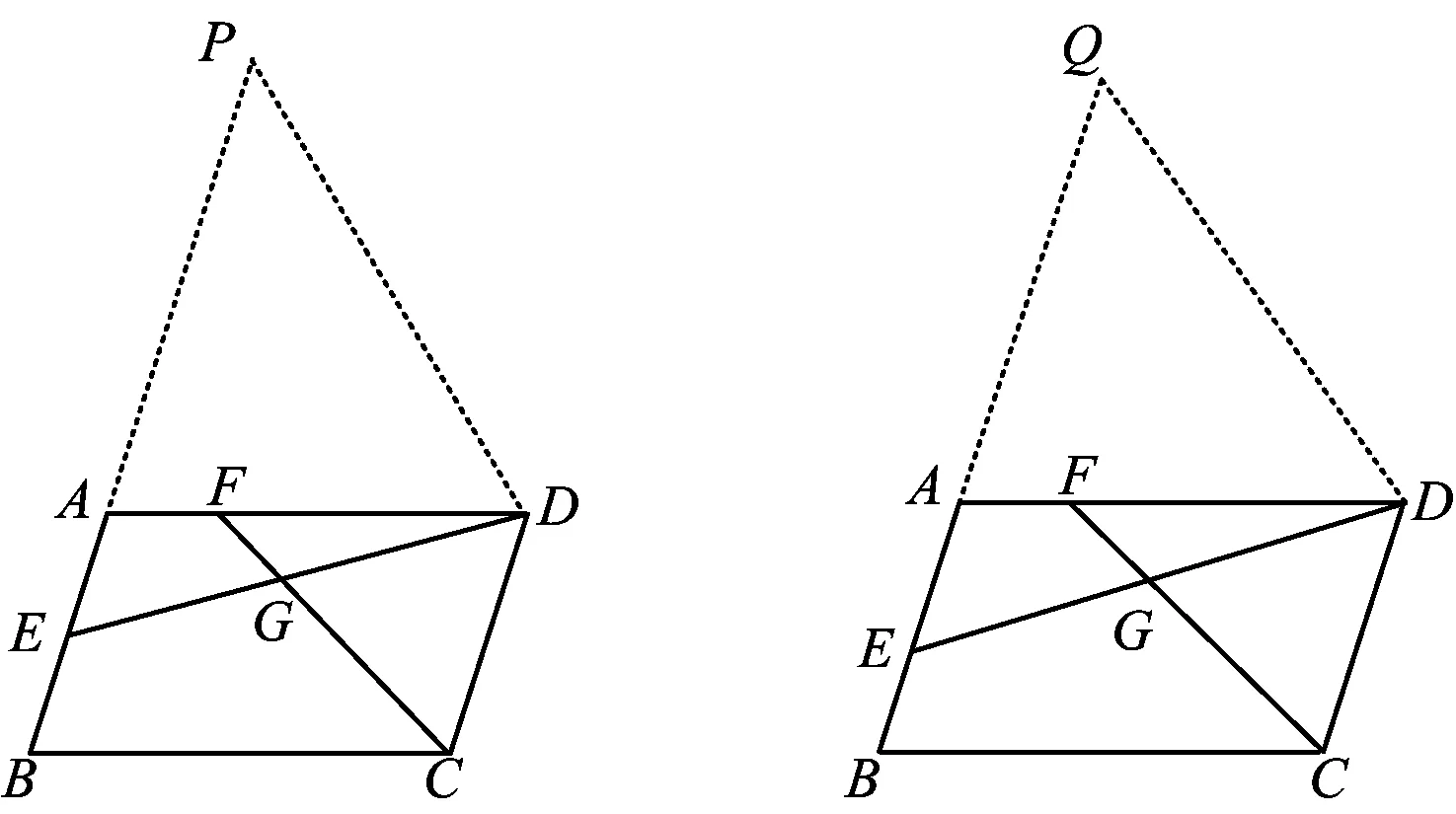
图7 图8

生9：我还有一种方法，如图8，在BA的延长线上取点Q，使DQ=DA，只需证明△QDE∽△DCF即可.

师：请生9谈谈你的方法与生8的方法有什么不同？

生9：构造的三角形位置不同，但都是抓住∠DAE和∠CDF的互补关系构造了与△DCF相似的三角形，因此本质上仍然是一致的.

教学说明寻找思维“愚钝”，自然引导点拨是解题教学的较高追求.将第1)小题中的矩形ABCD弱化为一般的平行四边形后，由于直角条件发生了改变，导致了其中一些角的关系和三角形相似关系随之发生了改变，有些关系仍然成立，有些不再成立，这也增加了本题的探究空间.实际教学中教师没有采取直接讲授或告知的方法，而是给足时间和空间让学生自主思考，大胆表述，充分暴露自己真实的思维过程，在此基础上，教师紧紧抓住学生的思维“愚钝”，通过自然引导、追问点拨，让学生在对比分析和新思路探寻的过程中加深对数学本质的理解.教师注重一题多解和多解归一，帮助学生积累解题经验、发展思维能力.

片断3筝形中线段比的探究.

师：真学课堂，精彩继续！来看将矩形变为筝形后的情况.

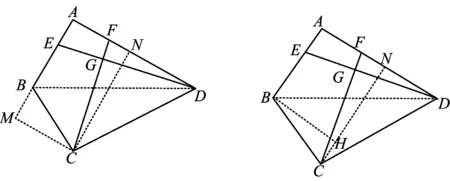
图9 图10

生11：我还有不同的方法，如图10，过点B作BH⊥CN于点H，构造Rt△BCH，接下去与生10的方法类似.

生12：我是在图9的基础上过点D作DQ⊥MC于点Q，如图11，构造△DCQ∽△BCM……

图11 图12

生13：我们组用的是面积法，如图12，联结AC，可以在△ACD中抓住面积的两种不同的表示方法来求CN的长……

生14：我们组想到的方法是在图12中，先证明△ACF∽△BDE……

师：刚才几位同学的方法都很好！这里涉及到的“转化”“方程”思想以及“面积法”等值得大家仔细领会和掌握.

图13

教学说明“拓宽解题思路，加深对问题的认识”是解题教学的重要职能.将矩形改成筝形后，问题的解决既可以通过“补形”类比于第1)小题用相似解决，也可以用“面积法”解决，还可以从“一般”与“特殊”的关系出发，考虑将线段放到特殊位置来考虑.在教学时，先让学生在独立思考的基础上进行小组讨论与交流，再由各小组派代表上台讲题，教师因势利导，根据课堂生成精讲点拨，帮助学生归纳解题方法，明晰数学思想.这样既注重一题多解和方法对比，又注重多解归一，把握通法，以解题为载体，使学生对知识的理解、问题的认识以及思维的发展得到同步提升.

3 教学思考及感悟

1)解题教学应从学生已有的知识基础和思维水平出发，寻找思维“愚钝”，追求自然引导.皮亚杰的建构理论告诉我们：学习不是被动吸收，而是学习者主动建构知识的过程.实践表明，一切教育教学行为，如果离开了学生的自我感知和主动内化，教师即使讲得再精彩，充其量也只是一场“个人秀”，并不能真正促进学生的自我发展.学生的思维具有个体化的特性，教师在教学中要认真分析学情，找准学生知识和思维的“最近发展区”，将解题方法的生成落在学生知识的最近生长点上，即：①要遵循学生的认知规律，把思考和探究的时间和空间更多的交给学生，把握好教学节奏，处理好解题教学的各个环节，从审题到破题再到思路的形成以及对解题过程的反思都要让学生亲自参与，引导学生积极主动思考，彰显他们的主体地位；②在此基础上寻找学生真实的思维“愚钝”，讲求对解题思路形成过程的自然剖析和引导，让学生体验思路的自然展开和方法的自然生成，避免简单告知或由教师包办代替.

在片断2的教学中，将矩形变为平行四边形后，由于一些角关系的变化导致图中一些三角形的相似关系随之发生变化，有的仍然成立，如△ADE∽△GDF，△DCF∽△GCD；有的不再成立，像△DCF与△GDF的相似关系改变，这直接导致了生4在类比生2用中间比进行转化时发生了思维“愚钝”，在这种情形下，教师没有急于直接告知，而是让出探究的时间和空间，给学生充分思考和表达的机会，再辅之以教师的自然引导，这才有了之后生5“换个角度思考”的精彩生成.这样的处理看似有些“浪费时间”，影响教学效率，但从长远看，这对于提升学生的思维品质、积累解题活动经验大有裨益.

2)解题教学应善于从图形中动与静的关系出发，作“特殊化”思考，进行“一般化”证明.数学是思维的科学，教学生“学会思考”是数学学科重要的育人功能，也是数学教学的重要职能.对于一些几何图形的变式类问题，有时直接发现或论证其中的一些结论会感到困难，对此教师若能抓住图形中动和静的关系，以“静”制“动”，引导学生从“一般”到“特殊”进行思考，先探究它的特殊或局部情况，从中发现规律与解答的方法，再进行一般化证明，往往是解决此类问题有效的教学策略.按照陕西师范大学罗增儒教授的观点，这种对于解题方法策略的指导是解题教学的精髓，也是促进学生数学核心素养形成的有效手段.

比如片断3的教学，教师若能引导学生抓住DE与CF的垂直关系，把图形“动”起来思考，然后在“动”中取“静”，找到两条线段各自的特殊位置(即BD和AC)，再结合特殊位置的关系来寻找思路，问题就会迎刃而解.再比如片断2的教学，在图6中，学生可能不容易想到用截取法，教师若能引导学生抓住∠A和∠EGF的互补关系将图形特殊化，使得DE向DA的位置运动，CF也随之运动，当DE与DA重合时，CF所在的位置(即图6中的CN)就为用截取法添置辅助线提供了思路.当然，这类问题用几何画板来演示往往比较直观，但学生在实际解题时没有几何画板可供操作，教师在进行教学指导时应帮助学生渗透和强化“特殊化”这一解题策略，促进学生从意识到能力的转变和提升.

3)解题教学应从题目蕴含的知识技能和思想方法出发，促进“深度”学习，提升数学素养.数学离不开解题，而数学题永远也解不完.这就要求教师不能满足于就题论题或蜻蜓点水，也不能热衷于搞题海战术，以多取胜.好的解题教学应当注重引领学生分析解题的方法，在问题解决的过程中帮助学生明晰隐含在题中的核心概念、基本性质、思想方法等，既授人以鱼又授人以渔，同时注重优化和培养学生的思维品质和思维能力[1].

本题通过对四边形中线段比问题的探究，着重研究了矩形及平行四边形的性质、相似三角形的判定和性质、等腰三角形及直角三角形的性质、一元二次方程等主干核心知识，同时考查了学生对类比、转化、分类、数形结合、方程(模型)等数学思想的理解和掌握情况，题目具有一定的典型性和综合性.数学思想方法是解决数学问题的利器，也是数学核心素养的重要体现，在教学中教师要充分挖掘题目的内涵，以知识为载体、思想方法为核心、思维和能力提升为主线，引导学生进行一题多解、一题多变及多解归一的学习训练，通过学生的积极参与、充分体验和解题后的反思，从而促进学生的“深度”参与和有效学习，帮助学生积累解题经验、提升数学素养[2].