运用构造思想提升高中生数学解题效率

朱海玲

【摘 要】本文简要介绍构造思想的思维特征，梳理构造法的主要类型，以例讲解构造法在高中数学中的应用，从已知条件和结论入手，通过构造新的数学形式将复杂的问题简单化，将陌生的问题熟悉化，从而巧妙地解决相关数学问题。

【关键词】高中数学 构造思想 多维发散 数量关系

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2018）06B-0159-02

构造法在高中数学中占据及其重要的位置，其核心方法是从已知条件和结论入手，并在此基础上构造出一些新的数学形式，借助此形式来解决一些相关问题。笔者在多年的教育教学经验中发现，构造法在高中数学的多个章节的知识中都有所体现，应用构造思想能够较好地提高高中生的解题效率，并不断促进其创造性思维能力的提升。

一、拔丝抽茧，认识构造思想的思维特征

构造法作为一种常见的数学解题方法，具有直观性、灵活性等诸多优点。对于高中阶段的学生来说，构造法能够极大地锻炼和培养其思维的多样性。教师在教学过程中应当通过对比构造、联想构造、归纳构造以及逆向构造等多种构造方式来逐步提升学生的思维活力，促进其创造性思维能力的提升。

在运用构造法进行解题时，应当认识到两点：第一，构造出的方程或者是命题等数学形式应当是在满足题中已知条件的基础上；第二，学生在构造时不能盲目构造，应当有明确的方向，并在此基础上进行构造。这样学生才能够深入认识到构造法的本质，并利用相关结论进行解题，不断促进其解题效率的提升以及数学核心素养的不断升华。

二、多维发散，梳理构造法的主要类型

构造法能够较大地培养学生的思维发散性能力，因此教师在教学当中要有意识地梳理构造法的主要类型，使学生能对号入座，见题知意。

（一）构造命题法，证明等价命题。对于某些命题来说，对其直接证明时学生可能会感觉无从下手，此时教师可以引导学生构造等价命题再进行证明。学生可以根据命题的某些特性，比如原命题与逆否命题等价来进行证明，或者是根据命题构造出熟悉的模型来解决问题，这样能够极大地简化证明过程。

对于这个题目来说，学生可以构造一个新的命题，原命题可以等价为把 10 个相同的小球分为四份，即在 9 个空中插入三个隔板，即 种。

由此可见，对于这种命题证明类型的题目，学生刚接触时不要操之过急，可以先认真思考是否可以构造其等价命题将其转化。这样做不仅能够极大地简化解题过程，而且能够全面提升学生解题效率和数学成绩。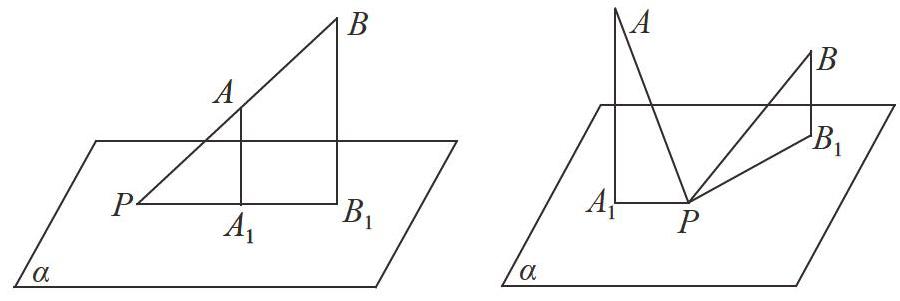

（二）构造新元法，求解三角问题。对于某些题目来说，其在解题时需要构造新的变量代入原式，尤其是三角函数，其诸多特性使得其经常作为新元被代入解决相关问题。这样可以将不熟悉的题目转化为熟悉的数学模型进行解答。这样做，在增强了学生的思维活力的同时也减小其思维跨度，促进其良好思维方式的形成。

对于这类相似的问题，教师可以引导学生构造新元，引入三角函数代换解决。这样不仅使思路清晰明了，而且能极大地简化解题过程，因此这种方法非常值得推广。值得一提的是，教师应当对题目中的注意事项和关键点给予重视和强调，争取做到万无一失。

（三）构造反例法，选择特殊实例。在某些题目中，尤其是选择、填空类型的题目，往往只需要学生得到最终结果，不需要太过详细的解答过程。对于这种题目，构造法无疑是一种很好的选择，学生可以通过构造一两个反例的方式来快速解题。

在教学选修 2-1 的 2.3《充要条件》的相关内容时，有这样一道题：

两条线段 PA、PB 与平面成角相等的充要条件是 PA=PB，试判断该命题是否正确。

对于这种题目来说，学生只要构造出一个范例证明该结论不成立，那么该命题即为假命题。在笔者的启发下，学生积极思考，举出了以下这两种反例推翻了该命题。如图所示，左图说明该命题的充分性不成立，右图说明该命题的必要性不成立。所以说对待这种类型的题目时，学生可以选取特殊值法构造反例来进行求解。这样做不仅节省时间，而且更有助于学生思维能力的发展。

通过这个实例不难看出，反例的构造能够快速地推翻该命题，得到该命题为假命题的结论。除此之外，学生还可以通过代入一些特殊值、点等来直接选择答案，提高解题效率。

三、多元实践，强化构造法的广泛应用

构造法在高中数学中的应用非常广泛，在向量、三角以及数列等多个章节都有所体现，教师在教学时应当对这种类型的题目进行归纳整理，使学生在应用的时候能做到得心应手、举一反三。

（一）构造向量，加强知识联系。知识之间往往是相通的，教师在教学时要注重对知识之间的联系进行梳理。比如，通过构造向量，学生能够巧妙地将三角函数的相关知识与向量相结合，灵活地解题，提升学生的解题效率，促进学生全面发展。

在教学必修 4 第二章《平面向量》时，有这样一道例题：

某平面上有三个向量 a，b，c，这三个向量都是单位向量，且 a，b 两向量相互垂直，问（a-c）（b-c）的最大值和最小值分别是多少。

在解答这道题时，学生可以根据题目中的“单位向量”“相互垂直”和“最值”等字眼联想到学过的三角函数的相关知识，这样学生就可以设 a（1，0），b（0，1），其数量积为零说明其相互垂直，满足题意，然后设 c 为（sinα，cosα），则（a-c）（b-c），再结合三角函数的相关知识不难得出：该式的最大值为 ，最小值为 。因此在遇到这种类型的题目时，教师要多引导学生学会构造向量，促进其对知识的迁移和应用，全面提升其解题效率。

（二）构造函数，培养创新精神。方程与函数向来都是紧密联系、密不可分的，所以在遇到与方程或者函数相关的题目时，可以在這二者之间进行灵活转化、构造。比如，将方程零点问题转化为函数交点问题等，这样不仅可以促进学生的知识迁移能力的提升，而且更有助于培养学生的创新精神。

在教学必修 1 第二章《指数函数》的相关知识时，由于指数函数相比于其他函数来说较为复杂，学生不好理解。于是笔者引导学生应用构造方程法来解决相关问题，比如：

x 满足方程 ex=3x+a，若此方程有实数根，求 a 的范围。

这种题目用以前的常规思路是不容易解答的，所以教师可以引导学生另辟蹊径。比如，构造两个函数，令 ex=f（x），3x+a=g（x），这样可以将 f（x）求导后求出斜率等于 3 时的切线方程，这样 a 的范围也就呼之欲出了。经过这个过程，把方程有实数解的问题巧妙地转化为函数有交点的问题，化抽象为具体，学生理解起来也更容易，更能有效促进学生创新性思维能力的提升。

（三）构造数列，探求解题捷径。构造数列法一般应用于数列求和问题中，该方法的应用能够极大地简化解题过程，提高学生的解题效率。这种类型的题目并不难做，我们需要让学生依据题干给出的关系式进行变形和构造，争取将其改造成我们熟悉的等差和等比数列的形式就行。这样我们就可以选择套用公式的方法来进行求解。

总之，构造法在高中数学中的应用非常广泛，对此教师应当分类进行总结，使学生掌握构造法在各种类型题目中的应用方法。通过构造新的数学形式的方式将复杂的问题简单化，将陌生的问题熟悉化。在解题时对症下药，巧妙解决相关数学问题。掌握这种方法能较快地提升学习效率，使数学成绩得到提高，使数学核心素养得到提升。

【参考文献】

[1]颜立平.运用构造法进行教学，培养学生创新能力[J].教师，2011（31）

[2]石富华，张姗姗，董永红.浅谈构造法在《高等数学》解题中的运用[J].九江学院学报，2009（3）

[3]刘良华.数学构造思想方法的探索与实践[D].武汉：华中师范大学，2004

（责编 卢建龙）