LBM-DEM四向耦合喷动床内介尺度模拟与分析

， ， ， ， ，

(华北电力大学 动力工程系，保定 071003)

1 引 言

喷动床具有气固接触时传热效率高、流形简单、操作压降低和便于处理热敏物质等优点[1]。研究喷动床内气固两相流，有助于揭示喷动床内颗粒剧烈而复杂的运动机理。研究两相流的方法主要有实验方法、理论分析和数值模拟。实验方法往往对实验设备要求很高，实验成本也较大，而且不能从微观上揭示颗粒的运动特性。理论分析一般只应用于通过合理简化能得到比较简单模型的体系，但随着体系复杂度的增加，其建模和求解难度会很大。随着计算机技术的快速发展，数值模拟克服了实验方法和理论分析的缺点，以其成本低和效率高的特点，引起了众多学者的关注。目前，用于模拟气固两相流的方法主要有欧拉-欧拉法和欧拉-拉格朗日法。其中，气相的求解都需要根据有限容积法等求解复杂的N-S方程，边界难以处理，且不易于并行计算。近些年发展起来的格子Boltzmann方法能够有效地克服上述传统数值模拟方法的缺陷[2]。

格子Boltzmann方法是20世纪80年代中期提出的一种从介观角度出发并基于分子动理论的数值模拟方法[3]。Filippova等[4]建立了格子Boltzmann方法与离散单元法的耦合模型，但采用单向耦合，只考虑了流体对颗粒的作用，忽略了颗粒对流体的作用。而Cui等[5,6]也主要分析了流体对颗粒的影响，颗粒对流体的作用分析较少。Govan等[7]虽然考虑了颗粒对流体的作用，但却只采用了双向耦合。Kruggel-Emden等[8]仅研究了颗粒和颗粒群对流体的作用。Lin[9]用三种不同的模型研究了鼓泡床中的气泡行为，没有深入探讨颗粒相的运动。Wang等[10]提出将格子Boltzmann方法与离散单元法耦合的离散颗粒模型，但其所采用的硬球模型将颗粒之间的碰撞视为瞬间刚性碰撞，无法给出碰撞的细节，且处理两个以上颗粒之间的碰撞问题具有一定的局限性。

本文将格子Boltzmann方法与离散单元法相结合，通过建立的介观尺度气固两相流LBM-DEM四向耦合模型，采用Fortran语言编程，以研究颗粒在喷动床内的流动特性作用机理，为喷动床的设计和优化提供一定的参考。

2 数学模型

基于LBM-DEM四向耦合的数学模型，考虑到固体运动对流场的影响，并参照文献[10]的处理方法，采用修正的格子Boltzmann方法模拟流场，采用Boltzmann理论计算控制体内流体受颗粒的作用力，将时驱硬球模型改为离散单元法软球模型处理颗粒间以及颗粒与壁面间的碰撞问题，将EMMS模型[11]改为Gidaspow模型[12]来计算颗粒所受曳力。

2.1 气相运动模型

标准的格子Boltzmann方法一般用来求解单向流体的流动。而本文考虑颗粒运动对流体流动的影响，所以需要在格子Boltzmann方程中加入附加碰撞相：

(1)

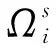
修正后的格子玻尔兹曼方程演变为

(2)

权函数B(εs,τ)和结构修正因子ω(εg)的表达式为

(3)

式中εs为颗粒体积分数,τ为无量纲松弛时间。

(4)

式中εg为气体的空隙率。

将大涡模拟(Large Eddy Simulation)应用到LBM可以模拟高雷诺数的流动[14]，即用湍流粘度系数υe来反映亚网格的小尺度涡对流动结构的影响。在Smagorinsky亚网格尺度应力模型[15]中，υe由应变速率决定,

(5)

式中Cs为Smagorinsky常数,Si j为应变速率张量。由文献[16]得,

(6)

式中ek i为离散速度ei在k方向上的分量,Qi j为动量通量。

通过τt=τ+τe代替式(2)的τ来实现LES应用到LBM，其中τe为有效碰撞涡松弛时间，则

(7)

由式(6，7)得到一个一元二次方程，求解得到修正后的松弛时间τt为

(8)

2.2 颗粒运动模型

采用牛顿第二定律描述颗粒的运动，单颗粒i的受力运动可以表示为

(9)

式中Fy,i为颗粒所受曳力，FP为颗粒所受周围颗粒的碰撞力。

颗粒之间的碰撞力由弹性力和阻尼力组成。法向力fn,ij分解为法向弹性力fcn,ij和法向阻尼力fdn,ij，切向力ft,ij分解为切向弹性力fct,ij和切向阻尼力fdt,ij[17]。

根据胡克定律，颗粒之间的作用力可表示如下。

颗粒所受法向力：

fcn,ij(t)=fcn,ij(t-Δt)-knΔδn

(10)

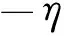
(11)

颗粒所受切向力：

fct,ij(t)=fct,ij(t-Δt)-ktΔδt

(12)

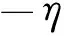
(13)

(14)

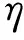
2.3 气固之间的耦合

采用牛顿第三定律解决气固之间的耦合问题。在一个控制体内，采用Boltzmann理论求解颗粒对流体的作用力[18]，用Gidaspow模型求解流体对颗粒的作用力。

颗粒对流体的作用力可表示为

(15)

流体对颗粒的作用力可表示为

(16)

(17)

颗粒雷诺数

(18)

为了减小二维系统与三维系统的差异，本文采用文献[19,20]提出的方法来计算空隙率，

(19)

式中 二维系统空隙率

(20)

控制体内流固之间的相互作用力以Boltzmann理论计算出的力为基准，因此要对Gidaspow模型计算出的曳力进行修正，来满足牛顿第三定律。计算标度因子为

(21)

通过标度因子对控制体内每一个颗粒受到的曳力进行修正：

(22)

利用上述模型，采用文献[21]的模拟参数，首先模拟了一段时间内射流在喷动床中的演化过程。整个过程与文献[21]的结果及文献[10]观察到的现象吻合较好。

3 模拟对象及参数

模拟对象在无量纲下为25×200×0.5的单孔射流准三维矩形喷动床，喷口宽度在无量纲下为2，模拟对象如图1所示。颗粒相采用2970个直径为135 μm的球型颗粒，密度为2500 kg·m-3。气相密度为1.1795 kg·m-3，气体粘度为1.8872×10-5kg·(m·s)-1。具体模拟参数列入表1。

本文模拟二维矩形喷动床内颗粒在底部中间射流作用下的运动过程。气体在壁面处设置为无滑移边界条件，颗粒在壁面处设置为滑移边界条件。

图1 模拟对象几何尺寸(无量纲)

Fig.1 Geometry size of the simulated object (dimensionless)

4 模拟结果分析

4.1 模拟序列图

在喷口速度为1.1 m/s时，0～1 s内颗粒流化过程如图2所示。随着射流从床层底部中心位置的喷口处不断射入，床中逐渐形成的气泡运动到床层顶部并发生破裂。颗粒在中间主气流的曳力作用下由床层底部向上运动，运动到床层表面，伴随着气泡的破裂开始向两边抛洒。两侧环隙区气流微弱，颗粒主要受自身的重力作用向床层底部运动。而床层底部颗粒受到中间气流的卷吸作用由两边向中间汇聚，运动到中间位置又随着主气流重新向上运动。以此循环，形成了喷动床中的环核流动结构。

表1 模拟参数

Tab.1 Simulation parameters

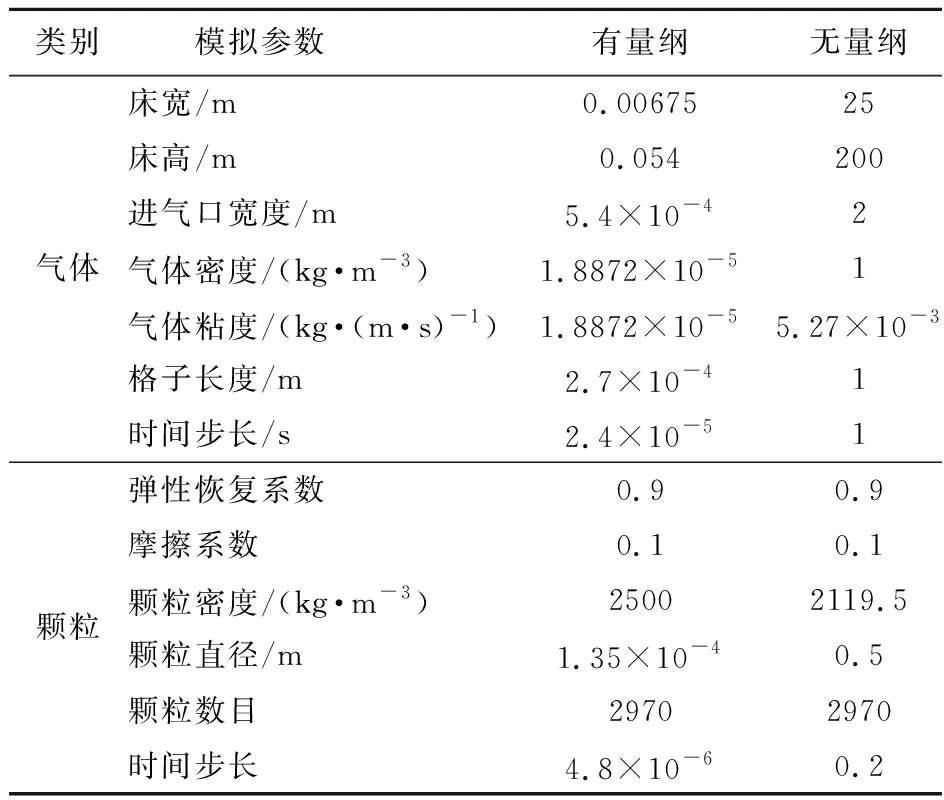
类别 模拟参数有量纲无量纲气体床宽/m0.0067525床高/m0.054200进气口宽度/m5.4×10-42气体密度/(kg·m-3)1.8872×10-51气体粘度/(kg·(m·s)-1)1.8872×10-55.27×10-3格子长度/m2.7×10-41时间步长/s2.4×10-51颗粒弹性恢复系数0.90.9摩擦系数0.10.1颗粒密度/(kg·m-3)25002119.5颗粒直径/m1.35×10-40.5颗粒数目29702970时间步长4.8×10-60.2

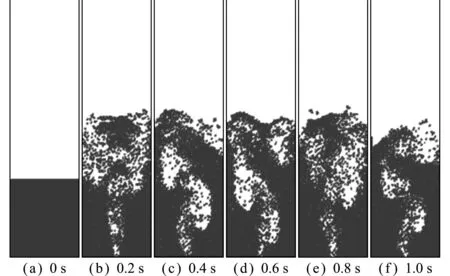
图2 模拟结果随时间序列图

Fig.2 Simulation results with time series

4.2 颗粒速度分布

0～1 s内，颗粒在不同射流速度和床层高度下水平方向速度的平均值如图3所示。颗粒水平方向速度大致呈左右中心对称，在床层较低位置的颗粒由于中间射流的卷吸作用由两侧向中间汇聚；在床层较高位置，伴随着气泡的破裂，气体能量逐渐耗散，颗粒所受曳力逐渐减小，速度也逐渐减小。当射流速度增加后，在相同床层高度处的颗粒速度变大，运动更加剧烈。

0～1 s内，颗粒在不同射流速度和床层高度下竖直方向速度的平均值如图4所示。在中间喷动区域，由于气流速度较大，颗粒所受曳力大于自身重力，速度向上，且随着高度的增加，气流的拖曳作用减弱，颗粒的速度也逐渐减小。而在两侧区域，气流速度较小，颗粒所受曳力小于自身重力，颗粒速度向下。当射流速度增加后，中间喷动区和两侧环隙区内的颗粒速度均增加。

4.3 气体速度分布

0～1 s内，气体在不同射流速度和床层高度下水平方向速度的平均值如图5所示。气体速度大致呈左右中心对称。气流从床层底部喷口射入，由中间向两侧发散，且随高度的增加，速度逐渐降低。当射流速度增加后，在相同床层高度处气体速度也增加。

0～1 s内，气体在不同射流速度下竖直方向速度的平均值如图6所示。两侧环隙区气体速度几乎为0，对颗粒作用较小，中间喷动区域气体速度向上，且速度较大，对颗粒的卷吸能力较强，同样随着床层高度的增加，气体速度逐渐减小。当射流速度增加后，中间喷动区气体的速度增加明显，而对两侧环隙区气体速度的影响较小，速度几乎为0。

4.4 床层膨胀高度

在0～1 s内，颗粒平均体积分数沿床高的分布如图7所示。本文认为颗粒平均体积分数为0时对应的床层高度为床层膨胀高度。随着床层高度的增加，床内气泡逐渐增多，颗粒的体积分数逐渐减小。当射流速度由0.9 m/s增加到1.1 m/s时，颗粒所受曳力变大，运动更加剧烈，床层高度由0.012 m提高到0.014 m。

4.5 床宽对颗粒速度的影响

考虑床宽对喷动作用的影响，将床宽分别增加到原床宽的两倍和三倍进行对比分析。当射流速度为1.1 m/s，床层高度为0.0108 m时，在0～1 s内，不同床宽下颗粒水平方向和竖直方向速度的平均值分别如图8和图9所示。床宽增加后，颗粒水平方向与竖直方向速度的变化趋势几乎不变，但速度的峰值明显降低。这是由于床宽增加导致左右壁面对中间喷动区射流扩散的约束能力降低，射流可以更容易向两侧环隙区扩散，颗粒所受曳力减小，运动能力减弱，水平方向与竖直方向速度的峰值降低。

图3 颗粒水平方向速度

Fig.3 Particle’s horizontal velocity

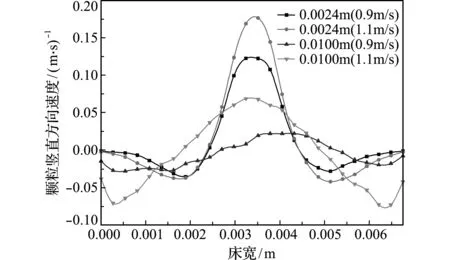
图4 颗粒竖直方向速度

Fig.4 Particle’s vertical velocity

图5 气体水平方向速度

Fig.5 Gas’s horizontal velocity

图6 气体竖直方向速度

Fig.6 Gas’s vertical velocity

图7 颗粒体积分数沿床高的分布

Fig.7 Distribution of particle volume fraction along bed height

图8 不同床宽下颗粒水平方向速度

Fig.8 Particle’s horizontal velocity in different bed width

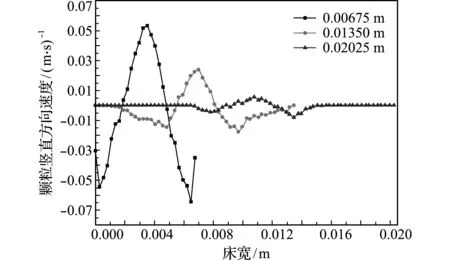
图9 不同床宽下颗粒竖直方向速度

Fig.9 Particle’s vertical velocity in different bed width

5 结 论

(1) 气流从床层底部喷口射入，形成气泡，并不断上升，在床层顶部破裂。中间区域的颗粒向上运动，到达床层顶端后向两边抛洒，在两侧环隙区颗粒向下运动，而床层底部颗粒向中间汇聚，从而实现了颗粒的内循环。

(2) 颗粒水平方向速度随床层高度的变化波动明显，而竖直方向速度却呈现出中间高、两边低的特点，在中间喷动区，颗粒速度向上，在两侧环隙区，颗粒速度向下；气体水平方向速度分布呈现中心对称，而竖直方向气体中间区域速度较大且向上运动，两侧区域速度较小，几乎为0。

(3) 颗粒平均体积分数沿床高逐渐降低，射流速度增大后，颗粒的运动更加剧烈，床层膨胀高度增加。

(4) 随着床宽的增加，颗粒速度的峰值降低。