避免核函数导数的二阶导数核近似方法的修正

·， ·江

(新疆大学 数学与系统科学学院,乌鲁木齐 830046)

1 引 言

SPH方法是Monaghan等[1,2]提出的发展比较快、应用研究最为广泛的无网格方法之一，最初用于解决天体物理学和宇宙学中模拟三维无界空间天体的演化问题。现在广泛地应用于计算固体力学[3]、流体力学[4]和多相流[5]等各个领域[6]。用经典的SPH方法进行计算模拟时，在边界处和不连续处有较大误差，其主要是由于此处的粒子缺失和粒子不均匀分布等因素造成的，于是便出现很多不同类型的SPH 核近似方法的修正[7-12]，以弥补传统SPH核近似方法的一些缺点，导致了SPH核近似方法表达公式的多样性[13,14]。

本文对已提出的避免核函数导数的二阶导数核近似方法SODF-SPH方法[15]进行了修正。首先，简单介绍SPH核近似方法的基本原理和计算函数导数的SODF-SPH方法；其次，在一元函数和多元函数的情形下给出计算函数二阶导数SODF-SPH方法的修正公式；最后，通过函数二阶导数的数值计算和热传导问题的模拟进行误差对比分析，从而验证该方法对提高计算精度和加快收敛速度的有效性。

2 传统SPH 方法

传统SPH方法的基本原理见式(1)，在区域Ω上定义的任何函数f(x)表示为

(1)

式中δ(x-x′)为狄拉克函数，定义为

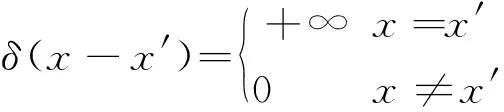
式(1)的狄拉克函数用光滑核函数W(x-x′,h)=(1/hd)W[(x-x′)/h]来代替，得到函数f(x)的核近似表达式

(2)

式中d为函数自变量的个数，光滑核函数依赖于两点之间的距离|x-x′|和定义核函数影响区域ΩW的光滑长度h,核函数影响区域在一维、二维和三维情形下分别为以x为中心的区间、圆和球，半径为κh，不同的核函数中κ取不同的值[16]。

考虑函数乘积的导数、格林公式及核函数的性质，n阶偏导数的核近似可表示为

(3)

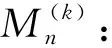
(4)

很显然M(k)n为常量，并不依赖于h。

将式(2)的f(x)在x处的泰勒级数展开式替换后得

(5)

由核函数的对称性和归一性得M0=1和M1=0，因此

〈f(x)〉=f(x)+o(h2)

(6)

同样的方法可以得到

(7)

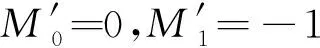
〈f′(x)〉=f′(x)+o(h2)

(8)

以此类推，

〈f″(x)〉=f″(x)+o(h)

(9)

很显然核函数影响范围在求解区域内时，核近似式(2)有o(h2)精度。式(2)中，当n=1时，有o(h2)精度；当n=2时，有o(h)精度。核函数影响范围不在求解区域内或接近于边界时，该SPH 核近似方法精度会降低，直接影响计算精度和稳定性。

(10)

(11)

粒子和近似式的精度不仅与核函数光滑长度h有关，而且与微元体的体积ΔV有关[16]。

3 函数导数计算的SODF-SPH方法

3.1 一元函数导数计算的SODF-SPH方法

由第2节讨论的函数核近似表达的基本思路可得

(12)

式中 如果核函数的影响区域未受求解区域的边界截断，由核函数对称性质有M3=0，此时解出f″(x)为

(13)

很显然，当核函数的影响区域没有受到求解区域的边界截断时，用式(13)得到的f″(x)的核近似式具有o(h)精度；否则不能保证o(h)精度。

3.2 多元函数偏导数计算的SODF-SPH方法

多元函数偏导数计算的SODF-SPH 方法与一元函数一样的思路相似，为表述方便，先引入与核函数光滑长度h无关的常量

U=x-x′，则

(14)

式中i和j为与函数自变量个数有关的哑标，l,k=1,2,…,d。

与一元函数类似条件下，有Milk3=0，此时由式(15)解出

Mlk2f(x)]

(15)

利用第2节讨论的SPH方法粒子和近似表示的基本思路，可以得出一元函数导数和多元函数偏导数计算的SODF-SPH方法核近似公式 (12，14)在粒子i处的粒子和近似表达式。

4 函数导数计算的SODF-SPH方法的修正

4.1 一元函数二阶导数计算的SODF-SPH方法的修正

(16)

由式(16)将f′(x)表示为

(17)

将式(17)代入式(12)整理得

(18)

式中M3=0时为一元函数导数计算的SODF-SPH公式(13)，由式(18)的推导过程可知，不论M3=0还是M3≠0，式(18)得到的f″(x)的核近似式均具有o(h)精度。

4.2 多元函数二阶偏导数计算的SODF-SPH方法的修正

对多元函数同样有

(19)

式中

(20)

式(20)代入式(14)，整理得

Bl kf(x)]+o(h)

(21)

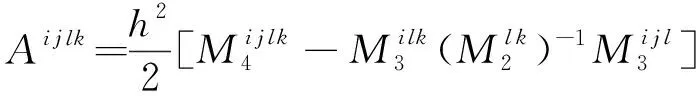
同样可以得出一元函数导数和多元函数偏导数计算的SODF-SPH方法核近似修正公式(18,21)在粒子i处的粒子和近似表达式。

5 数值验证和误差对比分析

定义在数值验证和误差对比分析过程中将要用到的误差的无穷范数、二范数和绝对误差为

(22)

(23)

ei=|fExact(xi)-fComputed(xi)|

(24)

其中M是求解域内的总粒子数，fExact(xi)和fComputed(xi)分别是xi处的精确值和SPH计算值。

本文所有数值算例，如果没有特别说明，计算过程中核函数的光滑长度等于粒子间距的1.2倍，使用的核函数是三次B -样条函数[16]。

5.1 函数二阶导数的计算

(1) 一元函数算例。考虑函数f1(x)=e- x2，f2(x)=sin(πx)，f3(x)=x3，x∈[-1,1]。

在区间[-1,1]上均匀分布不同个数的粒子时，用SODF-SPH方法和修正方法计算函数二阶导数所产生误差的二范数的比较列入表1。由表1可知，随着粒子数的增大，用SODF-SPH方法计算函数二阶导数的误差越来越大，其主要原因是随着粒子数的增加，在边界附近误差剧增。然而随着粒子数的增大，本文提出的修正方法计算函数二阶导数的误差越来越小，修正方法的误差远小于SODF-SPH方法。

数控专业是一门实践性很强的专业，其中涉及到很多抽象的理论知识，对于刚刚接触这些知识的学生而言，在学习时极易遇到一些困难。所谓数字化课程，其是将网络作为支持环境，运用数字化学习材料，使用数字化信息传递与人际交互方式的一种教学方式。在科学技术发展之下，数字化课程成为当前教育行业中一种新型辅助性教学方式，可以有效提升教学质量与效率。

当Δx=0.05，并在区间[-1,1]上均匀分布41个粒子，对不同的函数进行计算二阶导数时，用SODF-SPH方法和修正方法的误差二范数随着核函数光滑长度h的变化比较如图1所示，可以看出，本文提出的修正方法选择不同的光滑长度时，误差的变化不太大，且比SODF-SPH方法的误差小，即本文修正方法对提高精度起了很大的作用。

(2) 多元函数算例。考虑函数f1(x)=e- x2- y2，(x，y)∈[-1,1]×[-1,1]。

表1 一元函数二阶导数误差二范数的比较Tab.1 Comparison of error 2-norms in the second order derivative

在区域[-1,1]×[-1,1]内均匀分布1681个粒子，且Δx=0.05，Δy=0.05时，用SODF-SPH方法和修正方法计算函数对x的二阶偏导数，图2给出角落区域[0.85,1]×[0.85,1]内两种方法计算偏导数的绝对误差对比。可以看出，修正方法在边界附近的误差小于SODF-SPH方法，对其他类型的函数f2(x)=sin(πxy)和f3(x)=(xy)3，(x，y)∈[-1,1]×[-1,1]进行计算时，结论一致。

5.2 热传导问题的模拟

在直角坐标系下，瞬态热传导问题的控制方程为

图1 一元函数二阶导数误差比较

Fig.1 Comparation of error in the second order on one variete case

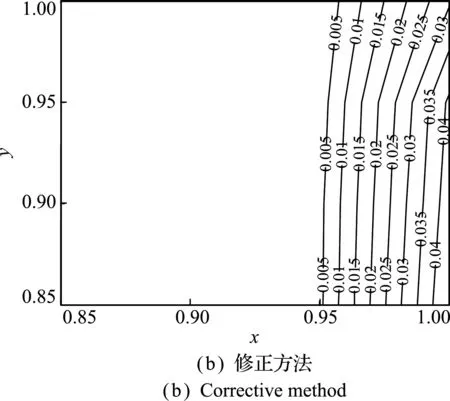
图2 多元函数二阶偏导数绝对误差比较

Fig.2 Comparation of absolute error in the second order derivative on multivariate case

(25)

初始条件为T(x,0)=T0(x)，x∈Ω

Dirchlet边界条件和Neumann边界条件分别为

T(x,t)=T1(t) (x∈∂ΓD)

T(x,t)·n+bT(x,t)=0 (x∈∂ΓN)

式中n为区域Ω边界外单位向量，bT(x,t)为边界热源，∂ΓD∩∂ΓN=Φ， ∂ΓD∪∂ΓN=∂Ω， ∂Ω为区域边界。

(1) 一维热传导问题的模拟

初始和边界条件分别为T(x,0)=T0，T(0,t)=T0，T(L,t)=T1，Q(x,t)=0。x∈[0,L]时，该问题有解析解[17]。

本文的模拟取L=1，T0=0 ℃，T1=1 ℃，并分别用SODF-SPH 方法和修正方法进行模拟，图3 给出设立了均匀分布的21个粒子，Δt=1×10-3s时,在不同时刻的数值模拟解与解析解的对比。结果表明，用本文提出的修正方法可以得到更精确的数值解。

(2) 二维热传导问题的模拟

二维热传导问题中边界和初始条件分别为T(0,y,t)=0，T(π,y,t)=π2，T(x,0,t)=x2，T(x,π,t)=x2，T(x,y,0)=x2+sinxsiny，热源强度Q(x,t)=-2，此时该问题对应的解析解为

T(x,y,t)=x2+e-2tsinxsiny

(26)

求解区域内均匀分布20×20粒子，时间步长Δt=1×10-3s时进行计算，图4为沿x和y轴方向在不同时刻的修正方法数值解和解析解。可以看出，修正方法数值解与解析解吻合良好。表2列出了修正方法与SODF-SPH方法的误差对比。可以看出,修正方法的误差比较小，提高了数值解的精度。

图3 不同时刻温度曲线数值解比较

Fig.3 Compare of temperature curve in different time steps

图4 温度随时间的变化分布

Fig.4 Temperature distribution in different time steps

表2 修正方法与SODF-SPH方法误差范数的比较

Tab.2 Comparison of error norms between the corrective method and the SODF-SPH method

t/sSODF-SPH方法修正方法L∞L2L∞L20.010.02189128240.00455192480.00011614460.00005520450.10.05614959190.01408896600.00097016550.00045266920.50.07057004720.02115713860.00215224800.00101575080.90.07510599540.02352524300.00173207510.0008219932

6 结 论

本文基于泰勒级数展开对已提出的计算一元函数函数二阶导数和多元函数的二阶偏导数的SODF-SPH方法进行了修正。将修正公式应用到一元函数的二阶导数和多元函数的二阶偏导数的计算和各种热传导问题的模拟，得出如下结论。

(1) 在粒子间距、核函数和光滑长度分别相同的情况下，对函数的二阶导数进行计算，本文提出的修正方法在提高SODF-SPH方法的计算精度和收敛速度方面起了很大的作用，特别在边界附近能有效地减小误差。

(2) 本文修正方法的计算量比原方法大，但任何点均具有o(h)精度。