多尺度嵌入式离散裂缝模型模拟方法

， ， ， ，

(中国石油大学(华东) 石油工程学院，青岛 266580)

1 引 言

多孔介质中精确有效的流动模拟对于了解地下资源的动态，实施有效管理有着重要的意义，如地下水、地热能源及页岩气开发项目等。这些大规模的地质构造，除了固有的非均质性，往往还包含复杂的天然裂缝。据不完全统计，世界上裂缝性油藏约占已探明总储量的一半；在我国，已探明的裂缝性油藏地质储量超过40亿吨，占探明总储量的28%以上[1]。而致密油气和页岩气等非常规油气资源，需压裂后方可商业开采[2]，压裂后也为裂缝性油气藏。

裂缝对流动形态有重要影响，因此裂缝的描述直接影响最终模拟结果的正确性。目前，主要采用双重介质模型、等效连续介质模型和离散裂缝模型作为裂缝性介质的流动模型。双重介质模型[3,4]是目前广泛应用的流动模型，但当存在数条控制流体流动方向和规模的大裂缝时，其计算结果误差较大。离散裂缝模型显示表征介质中的裂缝。现有的离散裂缝数值模型都是基于匹配型网格，由于裂缝分布复杂，往往基于非结构网格划分，其剖分过程繁琐，计算量大。尤其当裂缝相距较近时，网格剖分质量较差，导致计算误差。对此，Lee等[5-8]提出了嵌入式离散裂缝模型，对基岩直接进行结构化网格划分，然后将裂缝嵌入基岩网格系统中，并根据裂缝与基岩的相交情况形成裂缝网格，避免了上述复杂的非结构化网格剖分过程，大幅降低了计算复杂度。

然而，现有的嵌入式离散裂缝模型是基于有限差分法，当裂缝介质中裂缝分布复杂时，往往需要进行非结构化网格剖分，此时有限差分法并不适用。而且在规模较大的裂缝性油藏中，裂缝具有强烈多尺度性，为了得到精细解，需要进行较精细的网格划分，即便采用嵌入式离散裂缝模型，仍然可达数百万甚至数亿个网格单元。如果基于有限元法或有限差分法等传统数值方法求解此模型，巨大的计算量将超出当今计算机的计算能力。当前尺度升级法[9]广泛用于降低计算量，但是此方法无法充分利用小尺度精细数据信息，模拟精度不高。为此，需要一种既有尺度升级法的计算效率，又有较高计算精度的方法，多尺度方法[10-13]应运而生。

多尺度方法在粗网格上求解控制方程，在细网格上求解局部流动方程获得多尺度基函数，以捕捉小尺度流动特征。多尺度方法最初用于求解椭圆方程，其后应用于油藏数值模拟领域[14-16]，并随着该方法的推广，其逐渐应用于裂缝性油藏数值模拟[17,18]。且多尺度有限体积法[19]还用于求解嵌入式离散裂缝模型。但是多尺度有限体积法需要构建双网格结构，小尺度映射过程复杂。本文在多尺度模拟有限差分法的框架下，使用模拟有限差分法求解嵌入式离散裂缝模型的多尺度基函数，避免了使用复杂的双网格结构。本文阐述了多尺度算法的基本原理，建立了嵌入式离散裂缝模型多尺度基函数的模拟有限差分计算格式，最后通过多尺度解和参考解的对比验证了方法的正确性和程序的鲁棒性。

2 嵌入式离散裂缝模拟

2.1 数学模型

假设流体等温渗流，基岩和流体不可压缩，且不考虑重力和毛管力的影响。流体在裂缝和基岩中的流动满足Darcy定律:

基岩系统

-·[(Km)·pm]=qm+(qm f/Vm)δm f

(1)

裂缝系统

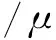
(2)

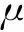
裂缝与基岩间的窜流量可以写为

qm f=-Tm f(pm-pf)

(3)

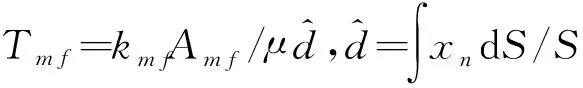
当裂缝相交时,裂缝间的窜流量可以写为

qf f=Tf f(pf i-pf j)

(4)

2.2 数值离散

基岩区域使用模拟有限差分法求解[20],该方法适用于任何复杂网格的计算,而且拥有良好的局部守恒性。由Darcy定律可知,对于任一个网格单元,其边界上的法向速度可以写为

vi=Ti·(eipi-πi)

(5)

式中Ti为传导矩阵;vi=[v1,…,vm]T,m为网格单元界面数;ei=[1,…,1]T;pi为单元压力;πi为边界面压力。裂缝系统采用隐式差分求解,由方程(2)可得

Tξ i +1/2(pf i +1-pf i)-Tξ i -1/2(pf i-pf i -1)=

ffi+qm f i+qf f iδf f i

(6)

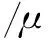
ff i=Vf iqf i

将基岩系统和裂缝系统耦合在一起可以得到嵌入式离散裂缝模型的模拟有限差分数值计算格式：

(7)

式中Tm f i=[Tm f i]为第i条裂缝与基岩窜流系数矩阵,Tf f=[Tf f]为裂缝之间的窜流系数矩阵，Tf i和pfi分别为第i条裂缝的有限差分传导系数矩阵和裂缝单元压力列阵。

3 多尺度计算格式

多尺度计算方法包含两套网格系统,如图1所示。其中,细网格系统包含岩石及流体性质等参数,粗网格单元由相互连接的细网格组成。

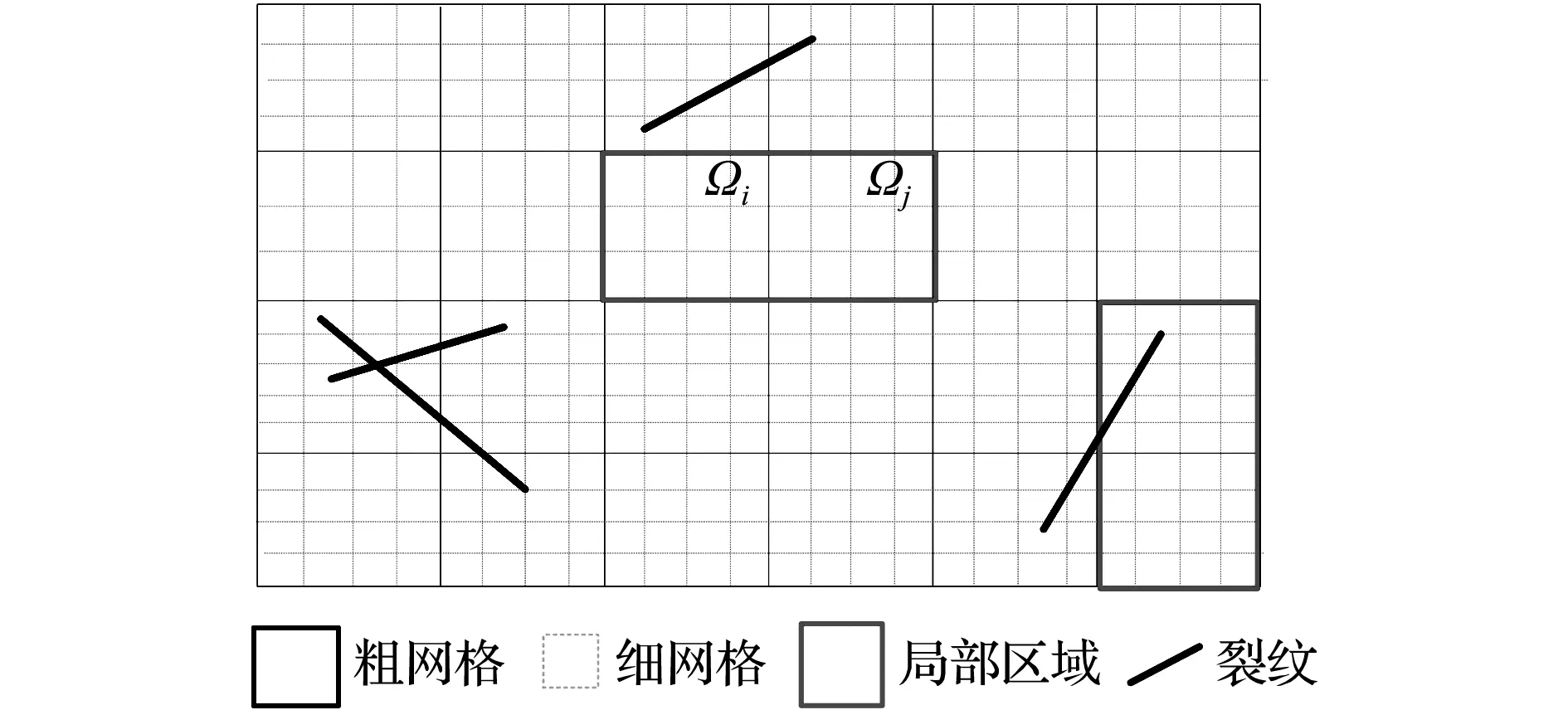
图1 多尺度粗网格示意图

Fig.1 Schematic of the coarse gridcells

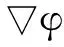
(8)

(9)

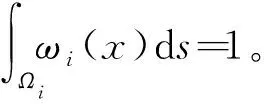
(10)

式中σ(x)=trace[K(x)]/d。将速度基函数表示为局部区域速度值的列向量,将压力基函数表示为局部区域压力值的列向量。

当粗网格单元内包含裂缝时,采用嵌入式离散裂缝模型表征裂缝单元。通过求解方程(11，12)可以获得多尺度基函数,捕捉裂缝及基岩流动特征。

(11)

(12)

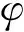
计算多尺度基函数后,为了得到粗网格方程,要将局部区域的多尺度基函数分为两部分：

Ψi j=ΨHi j-ΨHj i

(13)

满足

(14)

多尺度方法的一个显著特点就是易于进行小尺度映射,即细网格上的速度和压力可由对应的多尺度基函数经过拓展得来。对于小尺度速度,vf≈Ψvc,对于小尺度压力,

pf=Ip+ΦDλvc

(15)

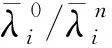
粗网格表面压力πc可表示为

(16)

由式(15,16)可得粗网格方程为

(17)

式中Bc=ΨTBfΨ,Cc=ΨTCfI,fc=ITqf,Dc=ΨTCfJ。求解粗网格方程之后,可通过式(15)得到小尺度解。

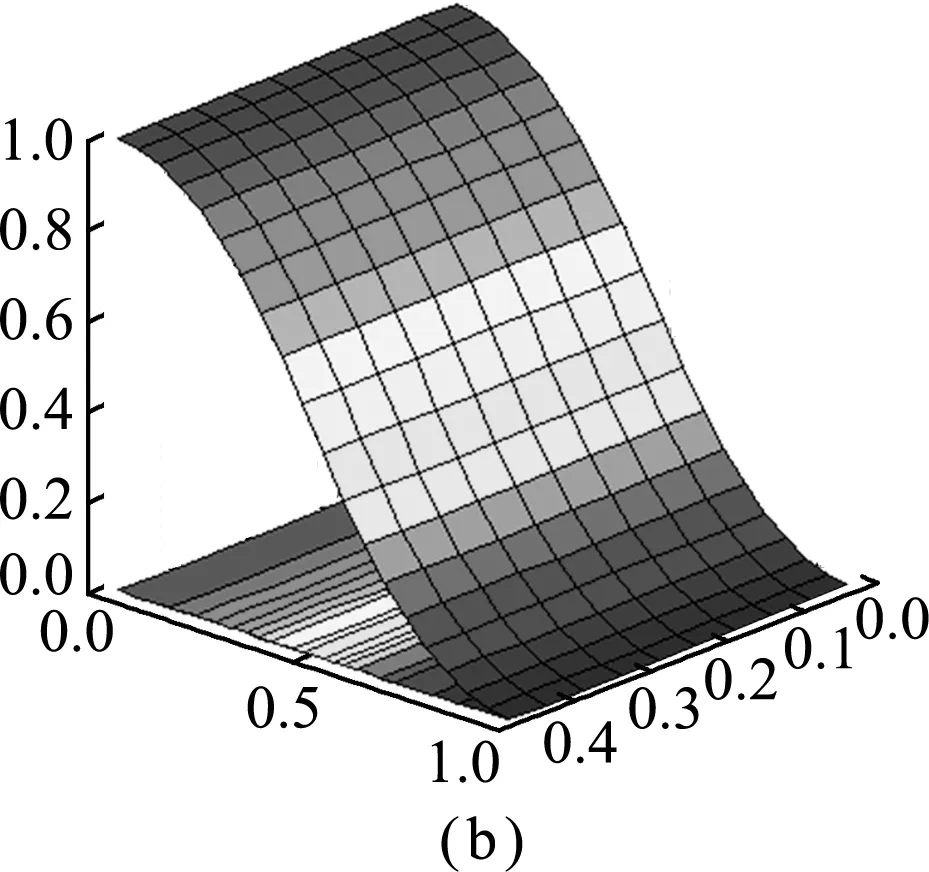
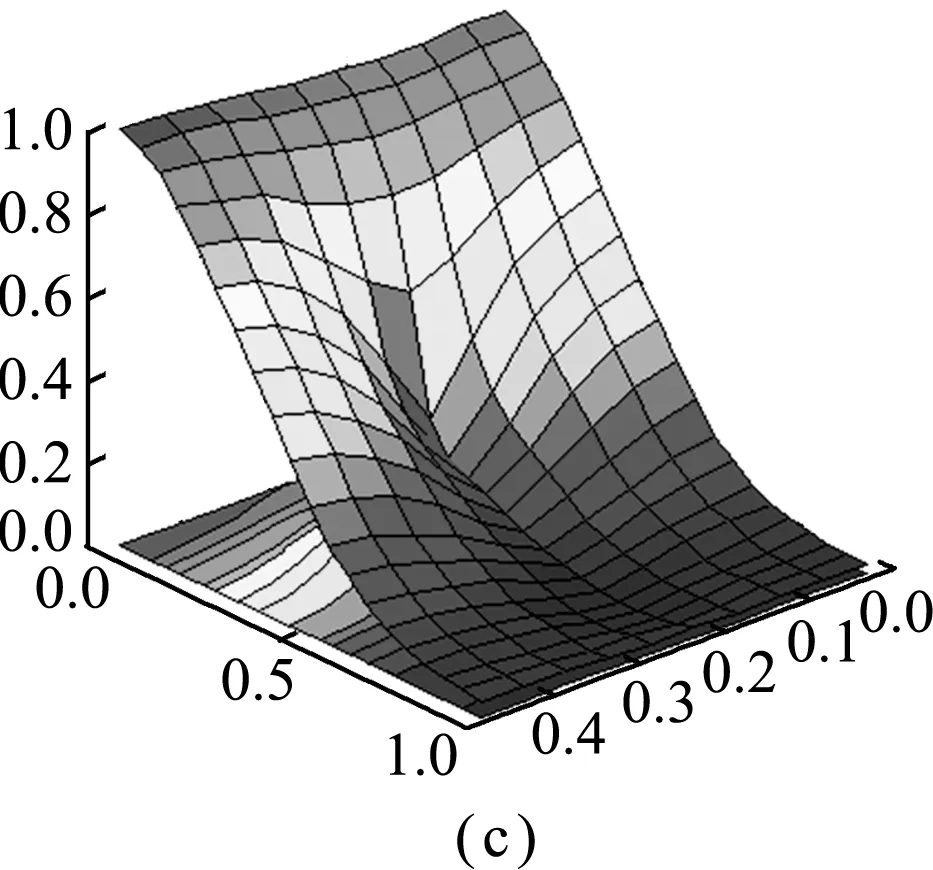
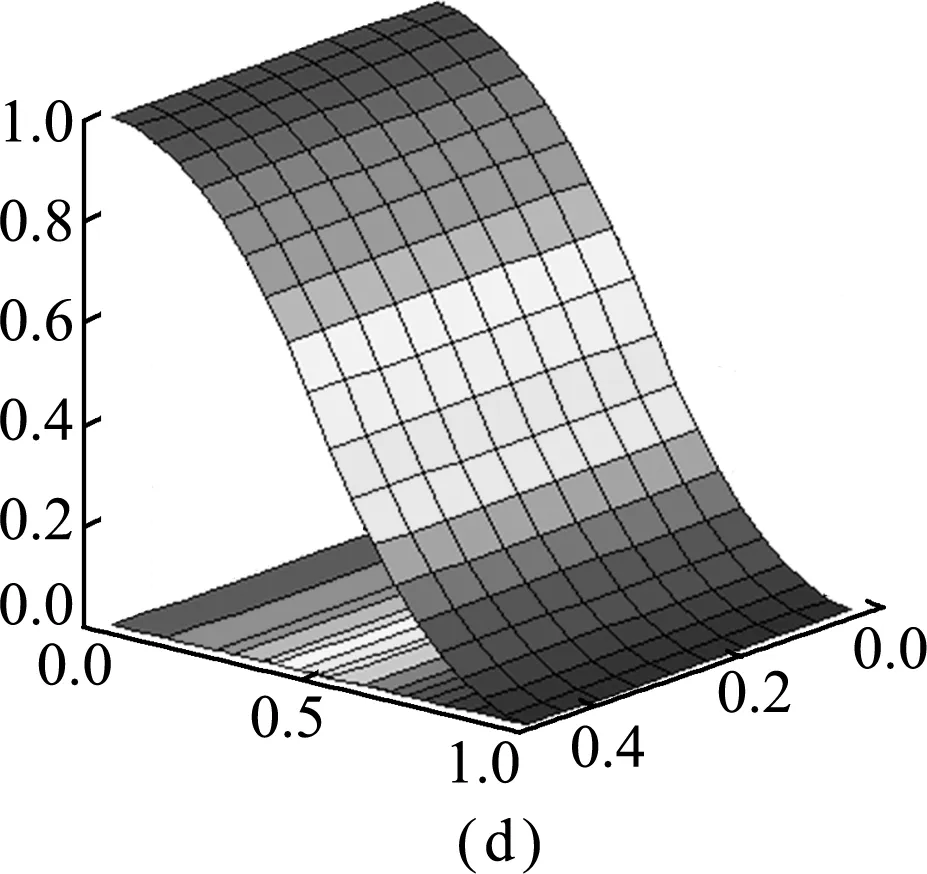
图2 目标粗网格单元的4个多尺度压力基函数

Fig.2 Illustration of all four pressure basis functions of a coarse gridcell

4 数值算例

4.1 均质嵌入式离散裂缝模型算例

考虑二维离散裂缝介质包含两条垂直相交的裂缝,如图(3)所示。研究区域大小为1×1 m2。裂缝与基岩的渗透率比Kf/Km=105,基岩是均质各向同性,孔隙度为0.2,裂缝开度为4 cm。区域上下边界为不渗透边界,左右边界为定压边界。细网格划分为40×40,粗网格划分为10×10。

图4(a)给出了40×40的网格划分下使用模拟有限差分法得到的压力分布,图4(b)是10×10的粗网格下多尺度方法得到的压力分布,图4(c)是多尺度方法小尺度映射后的压力分布。对比三个压力分布可以看出,多尺度方法得到的压力值与参考解呈现相同的分布形态,小尺度映射后的压力分布与参考解的压力分布基本一致。同时多尺度方法的计算速度比传统数值方法提高了3.4倍,大大节约了内存,减少了计算时间。

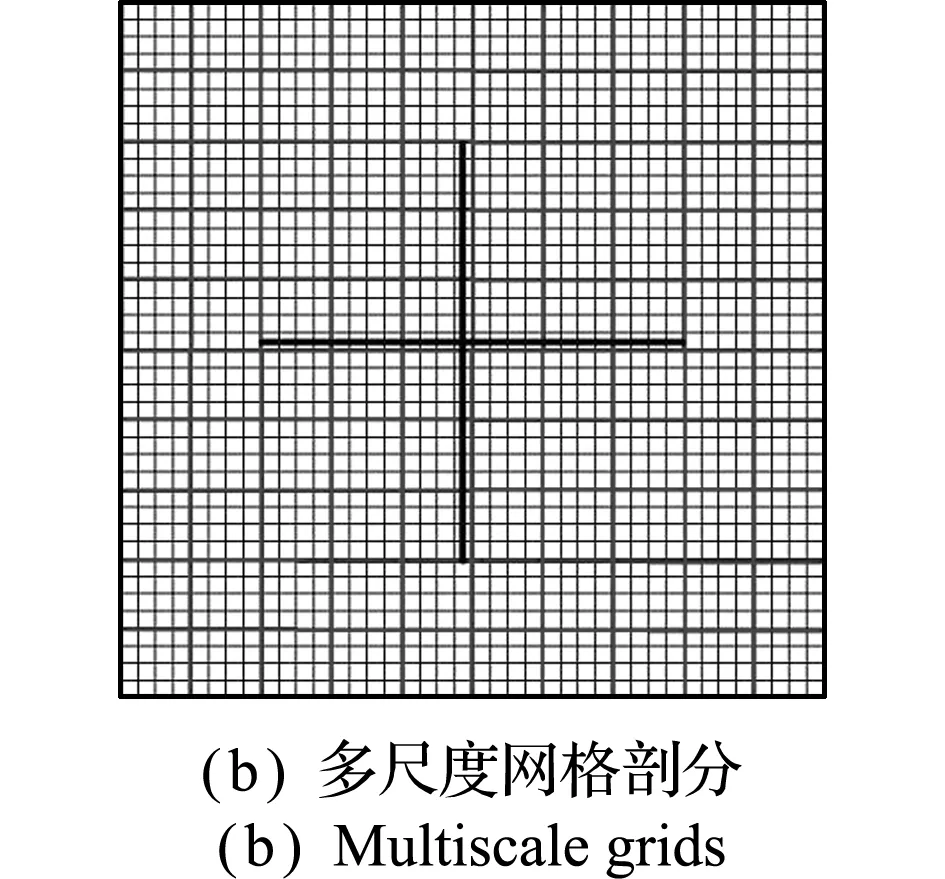
图3 裂缝模型及多尺度网格划分示意图

Fig.3 Illustration of the geometry and multiscale grids of the fracture model

4.2 非均质嵌入式离散裂缝模型算例

算例2是一个非均质介质,渗透率场如图5(a)所示,包含两条嵌入其中的裂缝,裂缝开度为 1 cm,网格划分如图5(b)所示。模型大小为10 m×5 m,小尺度细网格剖分包含40×20个网格,多尺度粗网格包含10×5个网格。区域上下边界为不渗透边界,左右边界为定压边界,右端压力为 1 MPa,左端压力为0。

图6(a)给出了40×20网格下的参考压力分布,图6(b)给出了20×10粗网格下多尺度解在小尺度映射后的压力分布。可以看出,多尺度方法不仅可以反映裂缝的压力,而且可以准确反映介质的非均质性。图7给出了介质在y=2.25 m上的参考解和多尺度解的速度和压力值对比。数值结果表明,多尺度方法在较粗的尺度上就可以获得较高的精度,验证了多尺度方法在处理非均质介质时的正确性和鲁棒性。

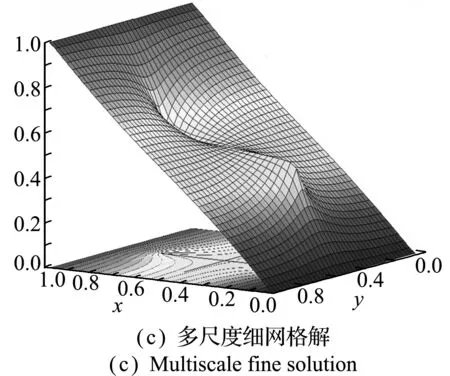
图4 参考解和多尺度解的压力分布

Fig.4 Pressure maps obtained by reference solution and multiscale method

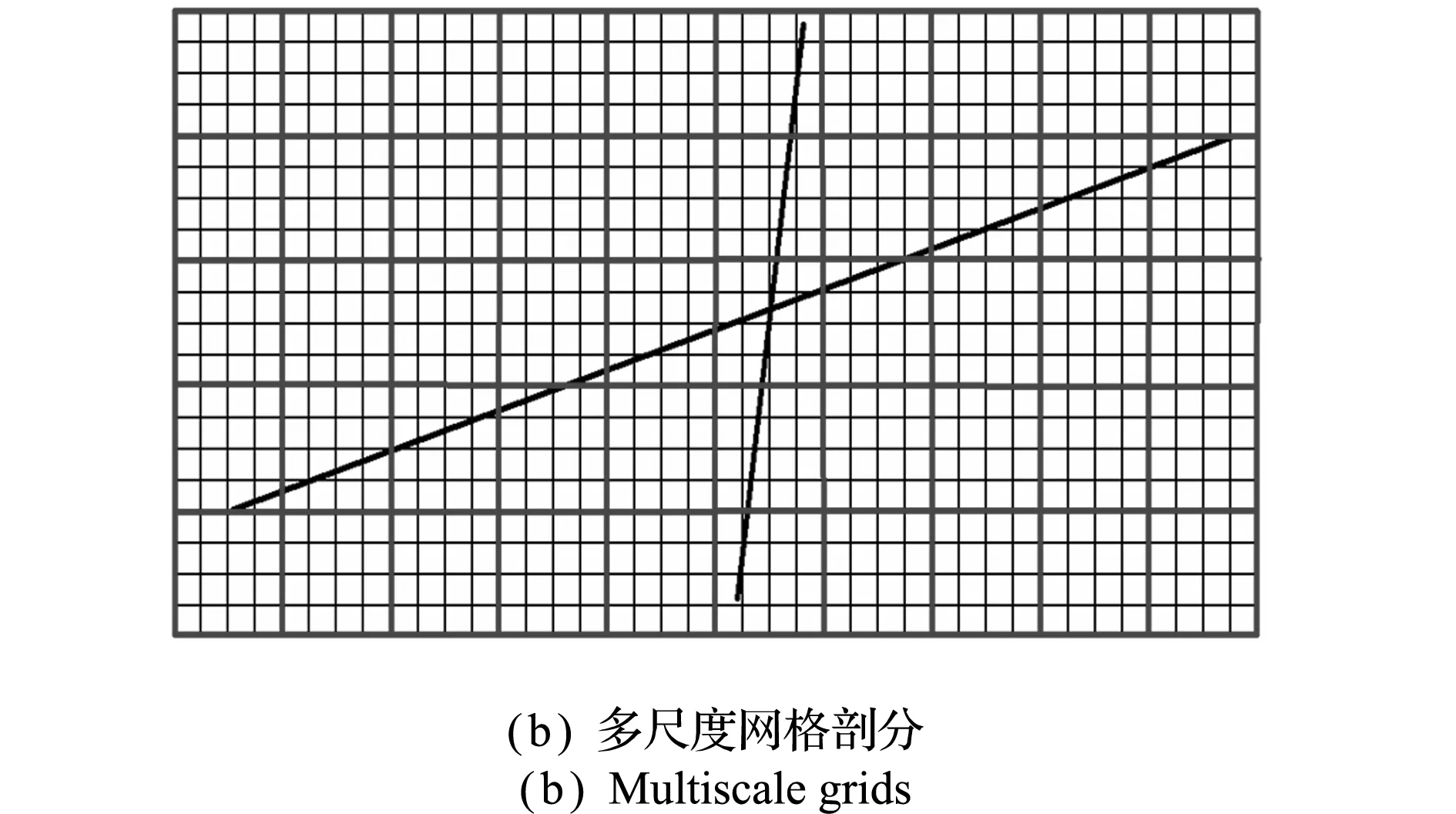
图5 非均质油藏嵌入式离散裂缝模型的渗透率场及网格划分

Fig.5 Permeability and grids in a 2D heterogeneous reservoir with an embedded fracture network

4.3 三维嵌入式离散裂缝模型算例

算例3是一个3D模型,如图8所示,区域大小为10 m×10 m×4 m。均质基岩渗透率为K=1 μm2,6条裂缝嵌入基岩中,裂缝开度均为1 cm。注入井位于左下角,生产井位于右上角。小尺度细网格剖分包含20×20×8个网格,多尺度粗网格包含5×5×4个网格。

图9(a)给出了三维嵌入式离散裂缝模型的压力分布参考解,图9(b)是多尺度方法得到的压力分布。采用相对L2范数表示压力相对误差：

ep=‖pf-pm s‖22/‖pf‖22

(18)

数值结果表明,多尺度方法与传统数值方法得到的压力相对误差小于0.106,同时计算速度提高了 3.1倍。与传统尺度升级方法不同,多尺度方法在大尺度上计算时,通过多尺度映射捕捉小尺度特征。图9 证明了多尺度方法模拟三维裂缝性油藏的正确性和高效性,具有用于开发新一代数值模拟软件的巨大潜力。

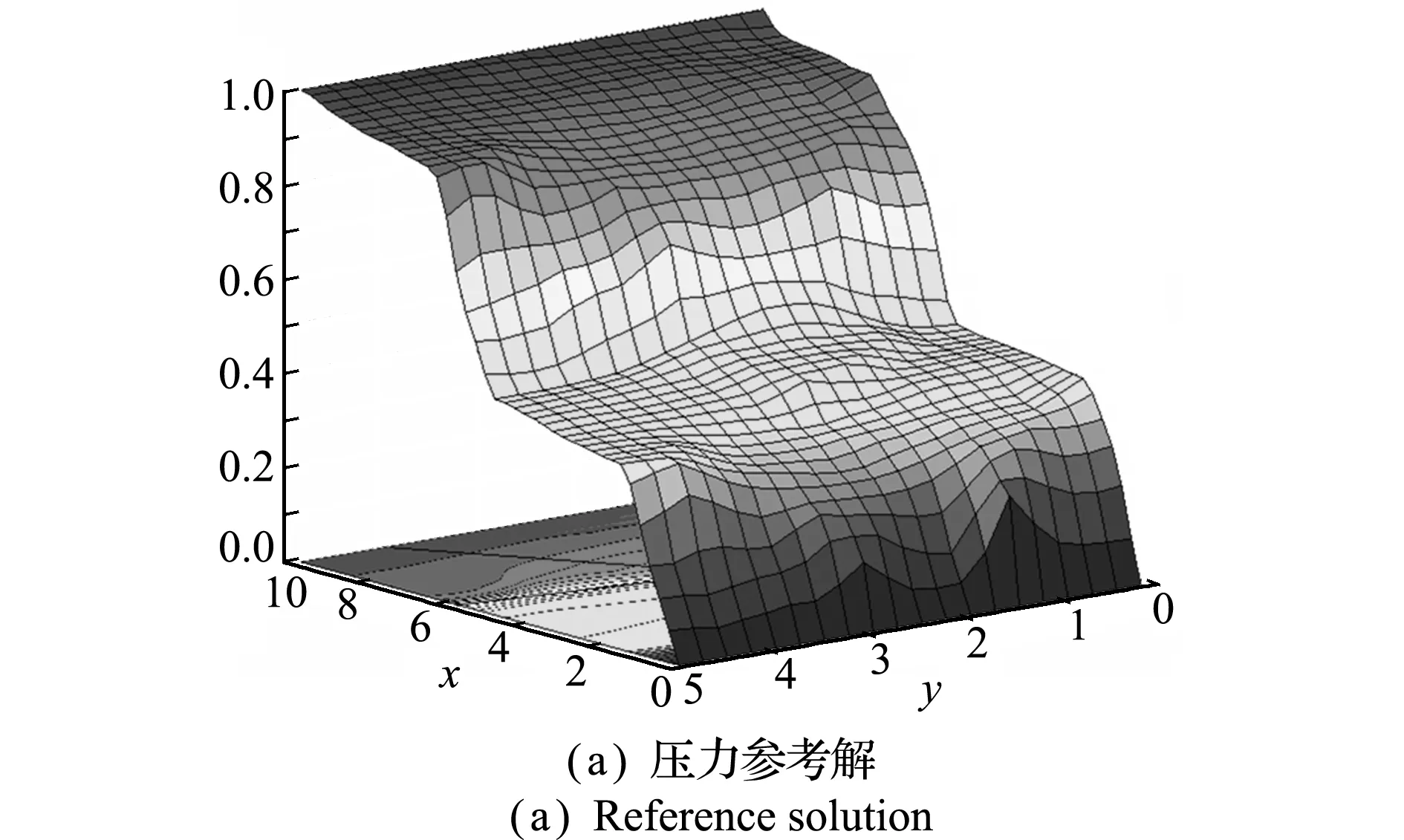
图6 参考解和多尺度解的压力分布

Fig.6 Pressure maps obtained by reference solution and multiscale method

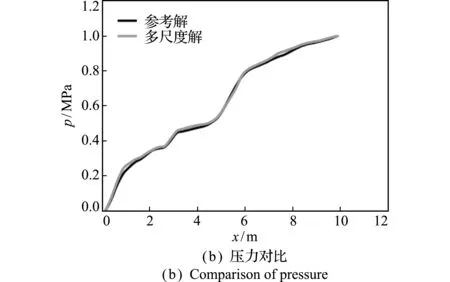
图7 参考解和多尺度解的压力对比与速度对比

Fig.7 Velocity and pressure comparisons for fine -scale and MsMFEM solutions aty=2.25 m

图8 三维裂缝模型及多尺度网格示意图

Fig.8 Illustration of the geometry and multiscale grids of the fracture model

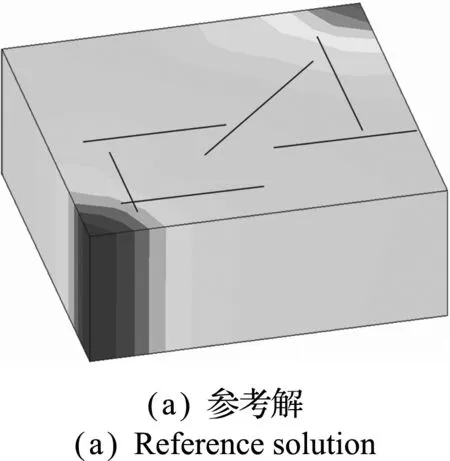
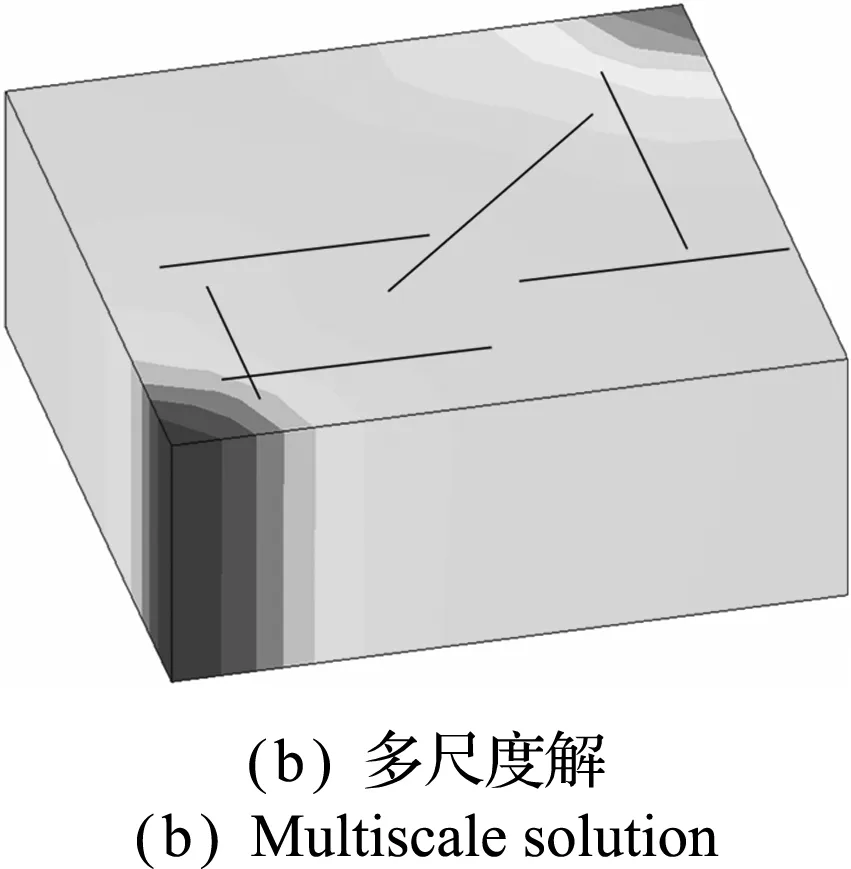
图9 参考解和多尺度解的压力分布

Fig.9 Pressure maps obtained by reference solution and multiscale method

5 结 论

(1) 离散裂缝模型显示表征介质中的每条裂缝,具有计算精度高、拟真性好的优点。但是传统的离散裂缝模型基于匹配性网格划分,造成网格剖分复杂且计算误差大。本文采用嵌入式离散裂缝模型,提高了计算效率。但是在大规模油藏数值模拟中,地质模型可能包含数百万甚至数亿个网格,采用传统的数值方法对其进行求解,仍然计算量巨大,将超出当今计算机的计算能力。本文提出嵌入式离散裂缝模型的多尺度模拟有限差分计算格式,在保证计算精度的同时大幅减小计算量。

(2) 在小尺度上使用模拟有限差分法求解嵌入式离散裂缝模型，准确获取了多尺度速度和压力基函数,并通过基函数映射得到小尺度解。得益于模拟有限差分的灵活性,可以处理任何复杂网格,为进行复杂地层模拟奠定基础。

(3) 多尺度模拟有限差分的基函数可以采用并行计算得到,进一步减少了计算量。因此,本文方法对于裂缝性油藏数值模拟有很高的潜在价值。