基于Kriging模型的频响函数有限元模型修正方法
, *,
(1.大连理工大学 工程力学系 工业装备结构分析国家重点实验室,大连 116024;2.大连理工大学 土木工程学院,大连 116024)
1 引 言
在土木、机械和航空航天领域,长期服役或极端环境可能对结构造成损伤,这些损伤积累到一定程度便会导致结构的失效,从而造成生命和财产的重大损失。因而,采用有效的损伤识别方法对结构进行监测和评估非常重要。
作为一种定量的全局损伤检测方法,基于有限元模型修正的损伤识别方法在近几十年得到广泛的研究和应用[1]。有限元模型修正的基本思想是,结构的有限元模型与实际模型往往存在一定的偏差,可以通过修改有限元模型的物理参数,使修正后有限元模型的响应与实际结构响应尽可能一致,从而提高模型的可信度。该方法原是用作结构数值模拟分析的前置工作,以确保构建的有限元模型的准确性和有效性,其在损伤识别领域中的应用主要是通过结构的动力响应对参数进行修正,以达到全局检测的目的,通过对比受损结构和未损结构或是受损单元与相邻单元在刚度质量参数上的差异来判断损伤的位置和程度,是一种同时完成损伤定位和定量的方法。
在早期的模型修正方法中,基于灵敏度的模型修正方法取得了较大成功[2]。在具体应用方面,根据所依据的不同动力响应,该方法可以分为基于频率、振型以及频响函数三大类别。其中,振型响应主要作为频率响应的补充,用以应对修正参数较多的情形[3,4]。而频响函数自身即可提供足够多的响应信息[5,6],但对测试环境要求较高,一定程度上限制了其应用。基于灵敏度的模型修正主要通过构建灵敏度矩阵来反映响应残差与修正参数的关系,灵敏度矩阵通过残差对参数的一阶导数求得,进而通过迭代的方式不断最小化残差,直到结果收敛,以达到模型修正的目的。模型修正方法可以看作一种优化问题,将残差作为需要最小化的目标函数,灵敏度法可以看作无约束最速下降法求解。此外,对于优化问题,直接使用人工智能算法,如遗传算法(GA)[7],也是有效求解手段,其优点在于不需要预知参数与残差的关系,同时可以对参数的变化范围加以限制,避免出现无意义的修正结果。
模型修正方法在工程应用中的主要限制之一是计算效率问题。理论上,有限元网络划分得越密,用以预测结构响应就越准确,模型修正的可靠性也越高。然而,更加密集的有限元网络将导致单次理论模型响应的计算时间急剧增多,如果模型修正程序需要足够多的迭代次数才能收敛,其所需的计算时间将放大到不可接受。
基于此,代理模型(或称为响应面法)作为一种快速的有限元分析替代手段,引起了众多研究者的关注。代理模型的核心思想是通过计算机仿真模型代替有限元分析模型构建参数与响应之间的输入输出关系。在确保了代理模型的准确度后,于迭代过程中直接通过代理模型计算理论模型的响应输出,以达到快速求解的目的。
目前,代理模型在有限元模型修正中的应用已经有不少成果。文献[8,9]使用响应面法进行模型修正和损伤识别,使用特定阶次的多项式拟合参数与响应的关系,通过合理的初始采样(使用D最优设计或中心复合设计),用最小二乘法确认多项式的待定系数,可以有效地利用少量采样点预测结构在不同参数下的响应。此外,为了增加响应预测点附近采样点的影响, Chakraborty等[10]使用移动最小二乘法求解响应面多项式的系数,并证明其对于响应的预测更准确。然而,该方法也导致响应面系数变为预测点位置的函数,在每一次预测中都需要重新计算,增加了收敛所需的计算量。Zhou等[11]比较了使用不同的径向基函数构建响应面的效果,并对一个大跨斜拉桥结构进行了模型修正。
此外,作为与高斯基函数相类似的一种特殊的响应面构建方式,Kriging模型在近年来受到越来越多的关注。Khodaparast等[12]使用Kriging模型建立了一个框架结构中两个梁的位置参数与频率的关系,用于快速进行区间模型修正,以界定参数的不确定性范围。胡俊亮等[13]使用Kriging模型对一座大跨度钢管混凝土连续梁拱组合体系桥进行了模型修正。Jin等[14]提出了一种顺序代理建模法,在一定量的初始采样点的基础上,对不同响应分别进行基于特定加点准则的响应面构筑。
上述方法大多选择了频率作为代理模型的输出响应,这主要是因为频率相对于不同参数的变化较为平缓,尤其是对多项式而言,其对于参数交叉项的影响并不敏感,因此通过少量的采样点即可得到较为精确的响应面。相较于频率而言,频响函数同样是模型修正的重要组成部分之一,可以提供更多的结构振动信息,但是其在代理模型中的应用却很少。因此,本文对使用频响函数作为代理模型输出响应的模型修正方法进行了研究,利用对非线性响应面模拟效果较好的Kriging模型建立其与参数的输入输出关系。为避免由于输入参数增加而导致所需采样点过多的情况,引入高效全局优化算法(EGO)[15]来实现模型修正的快速收敛,并将本文方法在两个数值模拟算例中进行应用,以验证其用于损伤识别的可行性及有效性。
2 Kriging模型
Kriging代理模型法是一种在数学和地质学中广泛应用的基于随机过程的统计预测方法,其构建的描述输入输出关系的函数主要用于计算机仿真模型的快速计算。对于一组给定的m个n维样本点输入X={x1,x2,…,xm}T(X∈Rm×n),和其对应的响应输出Y={y1,y2,…,ym}T(Y∈Rm×1),反应它们之间关系的Kriging模型的数学表达式为
(1)
式中 第一部分是数据的线性回归,通过p个多项式模拟响应面的全局近似;第二部分为服从正态分布N(0,σ2) 的随机过程。
需要说明的是,Kriging模型的基本假设是同样的输入会得到固定的输出。因此,对于响应输出与回归部分之间的偏差只因模型误差本身产生,无需考虑测量误差等随机因素的影响。该方法并不依赖多项式部分对响应面的模拟精度,而是着重于通过随机过程部分的有效填补来构建合适的代理模型,因而更适合处理非线性较强的问题,其他文献对Kriging模型的多项式部分经常取作常数。
对于随机过程z(x),Kriging假设所构建函数的真实响应面是连续的,任意两点随着距离的接近将趋向拥有相同的函数值,两点的z(x)同理。因此,任意两个样本点的z(x)之间的相关性可以表示为其空间距离的函数。这里采用应用最广泛的高斯相关模型:
(2)
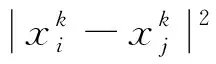
(3)
在此数学模型下,样本点真实响应出现的似然函数为
(4)
式中F为每个样本点处f(x)向量值组成的矩阵。
根据极大似然函数法,可以求得
(5)
(6)
在此基础上,极大似然函数的对数形式为
(7)
通过遗传算法求解该函数的最大值,即可确定不同维度上的衰减速率θk。
至此,一个联系样本点输入输出关系的Kriging模型构建完成。下一步则是对新点的预测。对于任意一点x0,遵循该点的预测值继续使样本点和预测点的似然函数极大化原则,可以得到其响应预测值为
(8)
式中rT(x0)为待求点与每个样本点之间的相关函数向量,
rT(x0)=[R(x0,x1),…,R(x0,xn)]
(9)
值得注意的是,对于第i个样本点响应的预测,由于rT(xi)R-1为第i阶单位向量,
(10)
因此,可以认为Kriging模型是一种插值技术,对于更详细的原理推导,可以参考文献[15]。
3 基于Kriging的模型修正方法
传统的基于灵敏度的模型修正方法是利用灵敏度矩阵将修正参数与响应的残差联系起来,灵敏度矩阵为响应残差相对于修正参数的一阶导数,然后通过使响应残差为0的方式迭代求解。但是,这种方法通常需要有限元模型全部自由度处的振型或频响函数测量值,对于不能满足条件的测点,则需要使用理论模型缩聚或是实验模型扩展来进行替代,在测点数远小于模型自由度数的情况下,将由于模型误差过大而失效。
由于基于灵敏度的模型修正方法可以看作是一种使用最速下降法求解的优化问题,因此,可以直接使用人工智能算法求解,该优化问题可以描述为
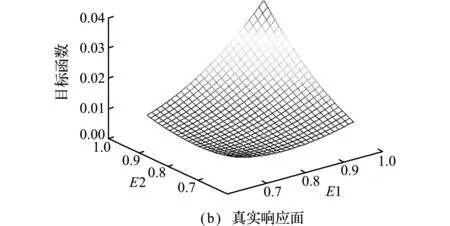
lbj (11) 式中wi为响应权重,n为响应个数,resi(x)为理论响应值,res*i为实测响应值,lbj和ubj为相应修正参数的上下限。在具体应用中,所有数值均应转换为无量纲量求解。 使用应用广泛的遗传算法求解上述问题,可方便地得到参数的修正结果。其优点在于,修正参数的范围变大,由于不需要计算灵敏度矩阵,许多灵敏度计算复杂或是无法计算的参数变得可以修正;其次是规定了参数的变化区间,可以避免参数收敛到无意义的结果上。 由于模型修正的参数间存在较强的互补性,导致模型修正的优化是一个典型的多峰值问题,如果修正参数较多,算法很容易收敛到一个局部解上。此外,该方法的核心问题在于,需要进行大量理论响应的计算来完成全局搜索。因此,利用Kriging模型代替原始有限元模型进行响应计算,可以在保留此方法优点的同时,显著提升其计算效率。 对于频响函数,为了构建平滑的响应面,将测点频响函数模值的对数作为输出响应,同时应避免使用参数变化空间内产生的共振频率作为频率点。但频响函数的响应面较为复杂,无法仅凭多项式部分进行精确拟合,因此只能通过足够的采样点来提升随机过程的预测精度。而足够精度的响应面所需的采样点个数将随修正参数数目的增多而快速增加至不可接受的程度。因而,直接构建频响函数响应面只适用于少量参数的情形。 由于只有优化问题的结果值得关注,而远离最优解区域的代理模型准确程度并不重要,因此,本文将优化问题的目标函数,即理论频响与实际频响残差的加权和f(x)直接作为响应输出,构建修正参数与该响应输出之间的Kriging模型,再使用高效全局优化算法EGO[15]来实现快速建模求解f(x)的最小值,其对应的输入参数即为参数的修正结果。 对于少量初始样本点构建的Kriging模型,可以通过增加样本点来提高其对于远离已有样本点位置的未知点的预测精度。由于本文的优化问题只关心最小值的位置,对于一定初始样本点构建的Kriging模型,可以仅在可能产生最小值的位置进行加点,即只提升有用区域的模型精确度,达到只使用少量采样点求解优化问题的目的。在具体的加点过程中,使用EGO算法具有较好效果,可以很好地平衡局部和全局搜索,避免优化结果收敛到局部极小值上,其原理如下。 对于Kriging模型,除了可以对未知点的输出进行预测,还可以对该预测值的准确程度进行评估。 (12) 在得到了未知点的预测值和均方差之后,EGO算法将该点的取值理解为一个均值为预测值、方差为均方差的高斯概率密度函数。该算法选择的加点位置并不是单纯的Kriging模型的最小值,而是计算Kriging模型中引入未知点对于已有样本点的响应输出最小值的提升的预期,并寻找该预期最大值的位置。 I(x)=ymin-y(x) (13) 式中 erf(·)为累积分布函数,ymin为样本点响应的最小值,I(x)为未知点的加入对最小值的提升,E[I(x)]为该提升的期望,通常未知点的预测值越小、方差越大,则E[I(x)]的值越大。因此EGO算法不仅会搜索Kriging模型中响应预测值最小的点,即求解局部极小值,还会加入响应预测值较小且预测准确度较低(均方差较大)的点,即进行全局搜索。本文对于最大期望所在位置的求解主要通过遗传算法来完成。 基于Kriging模型用于频响函数的模型修正的主要步骤可以总结如下。 (1) 根据拉丁超立方采样,生成一定数量的关于修正参数的初始样本点集。 (2) 运行有限元模拟程序,计算生成样本点的目标函数输出向量,并建立初始的Kriging模型。 (3) 使用遗传算法,计算当前Kriging模型中改进期望最大值所在的位置,并将其作为新加入的样本点。 (4) 计算新样本点的真实响应输出,并将其加入已有的样本点中,更新Kriging模型。 (5) 检验是否达到终止判据,达到则停止,并将输出向量中的最小值所对应的样本点作为修正结果;否则,回到步骤(3),继续加点运算。 Kriging模型的加点终止准则很多,本文选择改进期望的最小值作为判定依据,即Kriging模型将不断向未知区域进行探索,直到所有位置的对当前最小值的最大改进期望低于一个值。 基于Kriging模型的模型修正不仅继承了遗传算法不需要计算敏感度矩阵以及布置大量测点的特点,其优势还在于,首先算法会率先寻找当前代理模型下的最小值;然后,会受迫向可能产生更小值的区域进行探索,降低算法收敛到局部极小值的可能,且算法求解的精确程度易控。最重要的是,其对于有限元模型计算次数的需求远少于直接使用遗传算法。 首先通过一个3自由度的质量-弹簧系统来验证本文方法,如图1所示,理论模型中各参数的取值为 m1=1 kg,m2=3 kg, m3=1 kg k1=k2=k3=k4=k5=10 N/m,k6=30 N/m 假设实际系统中存在损伤,实验模型与理论模型的区别在于k2=8 N/m,k4=9 N/m,首先对两者进行特征值分析,得到其前三阶的频率,列入表1。接着以k2和k4的系数作为修正参数,其变化区间设为[0.5,1.5],以频响函数矩阵的H(1,3)分量作为参考响应,激振频率分别取0.5 Hz,1 Hz和1.5 Hz,其数目略多于修正参数的数量,以便验证两种方法在实验数据有限时的修正结果。需要注意的是,频响函数的激振频率应避免出现在自然频率随修正参数改变的变化范围内,否则,将会造成响应面的突变,增加代理模型的构建难度。 表1 3自由度质量-弹簧系统理论和实验模型的自然频率(单位:Hz) Tab.1 Natural frequencies of the analytical and experimental model of the three degree of freedom mass-spring system(unit:Hz) 模态阶数理论模型实验模型10.37070.351720.78900.773331.42351.4191 图1 3自由度质量-弹簧系统 Fig.1 Three degree of freedom mass-spring system 运用Kriging模型修正方法对参数进行修正求解,响应的权重均取为1,同时使用基于遗传算法的模型修正作为参考,对比两种方法修正结果的优劣。本文所有用到的遗传算法均使用Matlab自带的GA函数,没有加入适用于模型修正的改进,以验证Kriging模型修正在原始遗传算法上的效果。 在修正参数的变化区间里,采用拉丁超立方采样获取20个样本点作为初始样本。依次进行Kriging模型的修正步骤,终止标准设定为改进期望的最大值E[I(x)]<10-10时停止。仅经过8次迭代,Kriging模型便构建完成,如图2所示。 由于所需修正参数数量较少,仅适用于少量样本点即可构建足够精度的响应面。本算例中,Kriging模型构建的响应面与结构真实的目标函数响应面几乎完全一致。两种方法的修正结果列入表2,可以看出,两种方法均可得到较准确的修正结果,而Kriging模型的结果精确度较高。 对于这种参数较少,可以直接构建出精确响应面的问题,还可以直接将频响函数作为输出,分别构建每个频响函数的响应面,再通过遗传算法进行求解,同样可以大幅减少理论模型本身的计算次数,所构建响应面还具有可以重复利用的优点。然而,随着修正参数数量的增多,构建精确响应面所需样本点的个数也急剧增多。样本点个数是制约Kriging模型计算效率的关键,因为对每一个新点的预测都需要计算该点与所有样本点的相关性。因此,为保证计算效率,Kriging模型的样本点应尽量控制在500以下。由于频响函数随参数变化复杂,直接构建精确响应面可接受的修正参数数量最多不超过5,否则就必须依赖EGO算法来进行求解。 表2 3自由度系统的模型修正结果对比 Tab.2 Comparison of model updating results for 3 degree of freedom system 修正参数实际值Kriging误差/%GA误差/%k20.80.83534.410.85807.25k40.90.89750.280.89340.73 图2 3自由度系统的Kriging响应面 Fig.2 Kriging response surface of 3 degree of freedom system 为进一步验证本文方法在修正参数较多时的应用效果,使用一个悬臂梁有限元模型来进行修正。该模型长为0.9 m,截面惯性矩为9.135×10-10m4,材料的弹性模量为200 GPa,密度为7670 kg/m3,将其划分为9个单元,如图3所示。 本算例中,梁单元采用伯努利-欧拉假定,每个节点上有横向位移和转角两个自由度,假定结构存在损伤,造成了单元刚度的缩减,单元2减少20%,单元4减少30%,单元5减少10%。理论模型和损伤模型的自然频率列入表3。 以所有单元的刚度系数作为修正参数,其变化区间设为[0.7,1]。由于本算例要修正的参数多达9个,且参数之间的相互补偿状况较强,所以将参数的变化区间适当缩小,以降低响应面的构建成本,提高算法的收敛效率。 参考响应选取为频响函数矩阵的H(3,17)分量,激振频率分别取为10 Hz,45 Hz,115 Hz,220 Hz,360 Hz,600 Hz,760 Hz,1010 Hz和1300 Hz。这些激振频率基本都选在理论自然频率稍微靠右的位置,首先是因为这些位置的频响函数的变化较为剧烈,可以有效避免实际测试中模型误差和噪音误差的影响;其次构建响应面时,势必会考虑最极端的情况,即所有单元都达到理论的最大损伤,由于刚度降低,此时模型的自然频率较初始模型会产生较大的左移,为了避免激振频率与自然频率重合,必须将激振频率选定在初始模型两个自然频率之间靠右的位置。 表3 悬臂梁理论和损伤模型的自然频率(单位:Hz) Tab.3 Natural frequencies of the analytical and damaged model of the cantilever(unit:Hz) 模态阶数理论模型实验模型16.115.79238.2936.663107.26104.54210.41203.495348.63330.786522.95504.747734.98709.418985.66949.1491261.51210.95 图3 悬臂梁有限元模型 Fig.3 Finite element model of a cantilever 采用拉丁超立方采样获取90个样本作为初始样本,进行Kriging模型修正,终止标准不变。本算例中,Kriging模型经过179次迭代构建完成。由于参数的维数较高,仅将单元1和单元2的刚度系数作为变量,其他单元的刚度系数设为1不变,Kriging 模型预测的响应面与真实响应面的比较如图4所示。可以看出,当修正参数较多时,Kriging模型对于远离最小值附近的目标函数的预测误差非常大。但是,这并不影响Kriging模型给出满意的修正结果。两种方法的修正结果对比列入 表4。可以看出,Kriging方法修正的效果较好,而GA法则出现了明显的误判。 此外,本算例还比较了两种方法所需的理论模型有限元程序计算次数。分别使用前6,7,8,9个单元的刚度系数作为修正参数,两种方法所需的有限元程序计算次数列入表5。可以看出,基于Kriging模型的有限元模型修正需要的计算次数远比直接使用GA方法少得多。随着结构有限元模型的精细化和复杂化,直接使用GA方法所耗费的时间将变得不可接受,这也正是使用代理模型进行模型修正的意义所在。 表4 悬臂梁的模型修正结果对比 Tab.4 Comparison of model updating results for the cantilever 修正参数实际值Kriging误差/%GA误差/%E110.99570.430.99540.46E20.80.79540.580.78202.30E310.99940.060.98911.0E40.70.70991.390.810213.6E50.90.92182.360.92512.71E610.99900.10.904110.61E710.99080.9310E810.99140.870.96453.68E910.98931.080.96613.51 表5 两种方法所需的有限元模型计算次数 Tab.5 Number of finite element models required for the two methods 参数个数KrigingGA612810800713711000828811400926912000 图4 Kriging模型响应面与真实响应面的对比 Fig.4 Comparison between Kriging model response surface and real response surface 本文提出一种新的使用频响函数作为测量响应的模型修正方法。该方法主要通过构建Kriging代理模型来建立修正参数输入与响应残差之和的目标函数输出之间的联系,再通过全局优化算法EGO快速求解。该方法主要具有以下优点。 (1) 不需要已知修正参数与响应残差之间的关系,对于测点的位置分布同样要求较低,在算例中,只需要频响函数矩阵的一个分量即可实现修正目的,其应用的可行性和方便性优于传统的灵敏度方法。 (2) 可以通过控制终止标准来提高算法搜索的广度和深度,即便是使用未加处理的遗传算法,也可以显著提升修正结果的精确度。 (3) 由于使用了代理模型代替有限元模型进行优化问题求解,对有限元模型的计算需求大大降低,对于单次计算时间较长的有限元模型,计算效率显著提高。
4 数值仿真算例
4.1 算例1

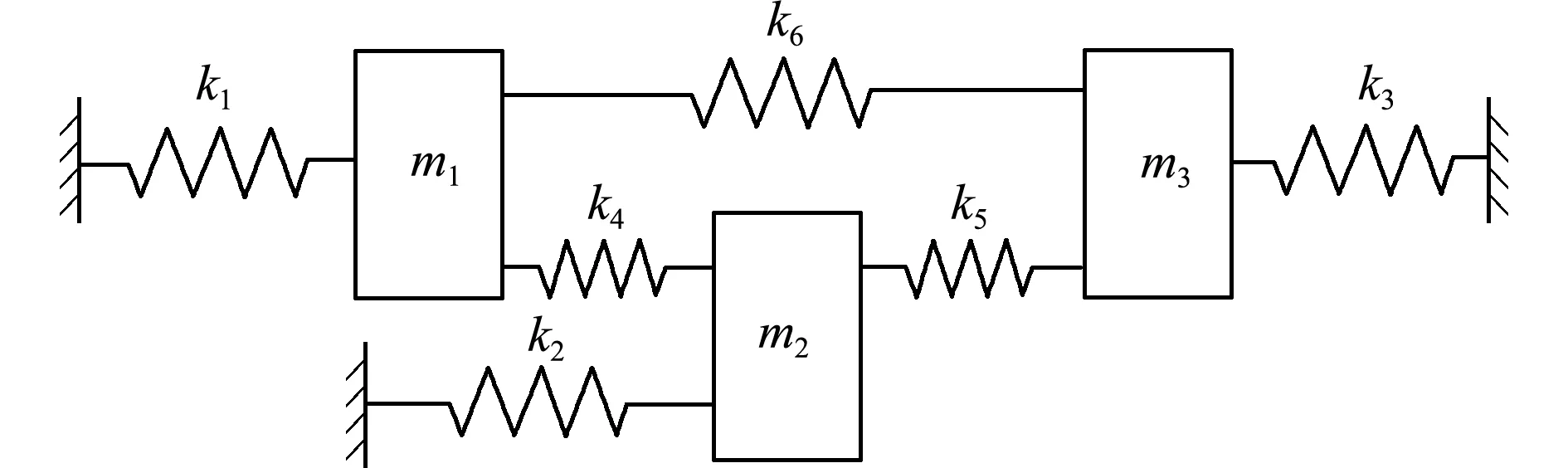
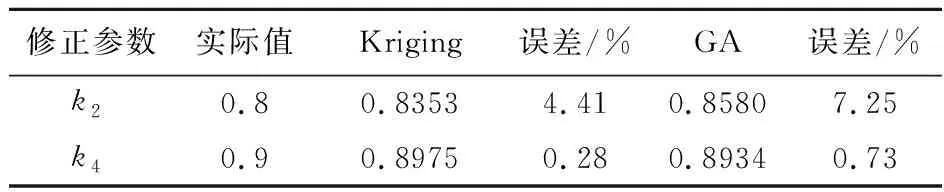

4.2 算例2


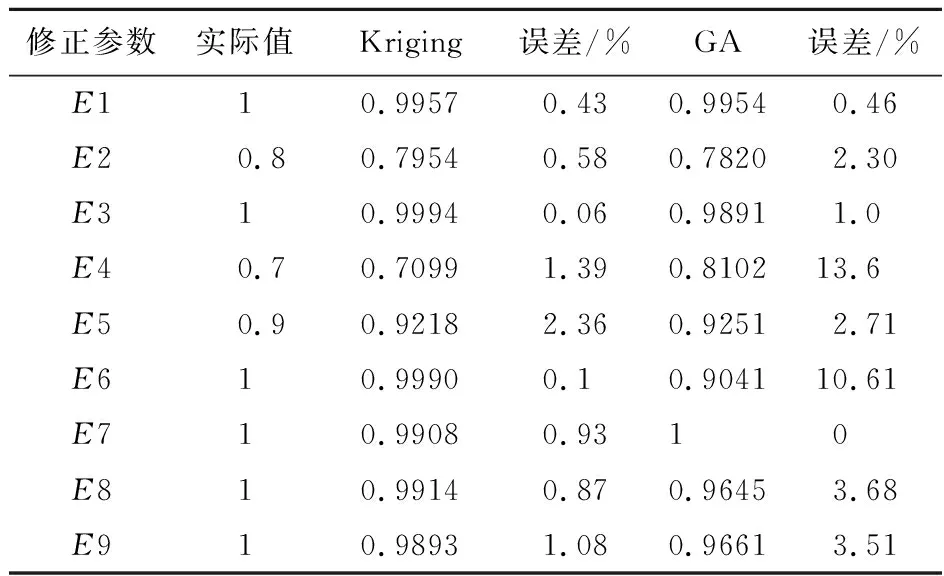


5 结 论

