粒子法中自由表面粒子识别

， ， ，

(清华大学 核能与新能源技术研究院，先进核能技术协同创新中心，教育部先进反应堆工程与安全重点实验室，北京 100084)

1 引 言

移动粒子半隐式法MPS(Moving Particle Semi-implicit Method)是一种基于拉格朗日Lagrange粒子的无网格方法，最早由Koshizuka等[1-3]提出，并随后运用于计算核能领域的一些热工水力难题，如蒸汽爆炸、两相流和液滴破裂等大变形问题及复杂的流固耦合问题。上述问题如果采用传统的网格方法进行模拟，在计算过程中容易出现网格变形挤压，从而造成计算不收敛。而MPS方法完全克服了上述困难，采用完全的Lagrange方法进行模拟计算，粒子之间通过核函数产生相互联系，采用梯度模型和拉普拉斯模型等离散控制方程，由于粒子之间没有拓扑关系，所以对自由表面变化非常剧烈的物理现象能够进行较好模拟，也能够取得较好的计算结果。

由于MPS方法发展时间较短，仍存在一些缺陷。比如在传统的MPS方法中，一直没有解决如何准确判定自由表面粒子的问题，而这一问题也是导致在MPS方法计算中压力计算出现震荡的原因。Lee等[4]发现，MPS方法在判定自由表面粒子方面存在缺陷，比如容易将流体内部较稀疏区域的粒子识别成自由表面粒子；在计算过程中，流体内部压力变化不均匀，在局部会出现压力突变，从而导致流体内部压力振荡和由于压力振荡导致的流体表面粒子飞溅。

针对基于Lagrange方法的粒子法中自由表面粒子判定问题，其主要方法可以分为几何法和体积法两类。体积法方面，Randles等[5]对存在破碎的物质运用SPH方法进行模拟时，通过采用重正化的核函数来改进离散误差，从而解决了在自由表面接触处密度不连续的问题，改善了自由表面的判定；Lee等[6]在对比WCSPH方法和ISPH方法时，对自由表面边界条件进行了改进，通过粒子的位置散度大小来确定粒子是否为自由表面粒子，该方法能判断出大部分自由表面粒子，但还有小部分自由表面粒子无法确定；Tanaka等[7]在研究MPS方法中的压力振荡问题时，通过重新构造自由表面处的粒子数密度和初始粒子数密度的方法，改进了自由表面粒子的判别，一定程度改善了MPS计算中的压力振荡问题。几何法方面，Dilts[8]在开发全新的MLSPH方法时，针对该方法在收敛性方面存在的问题，开发了全新的基于几何方法的自由表面粒子判定方法，并通过对球形与平面碰撞的模拟验证了自由表面判断的改进；Haque等[9]借鉴Dilts的基于几何方法的自由表面粒子判定，将该方法扩展到了三维，并进行了三维的球与平板碰撞模型计算，取得了良好的结果，但计算过程复杂，计算时间较长；Shibata等[10]对MPS方法开发新的压力梯度模型时，通过光照法来判断自由表面粒子，模拟容器内静止的流体时取得了良好的效果，但是这种方法不适用于运动的流体。

Marrone等[11]对SPH方法中的自由表面粒子判定进行了深入研究，首先通过求解重正化矩阵的特征值，初步筛选出自由表面粒子；然后通过几何法，将第一步误判的自由表面粒子剔除；使用该方法对溃坝模型进行了模拟，取得了良好的结果，但是求解重正化矩阵较为复杂。也有一些学者通过修改计算参数来识别自由表面粒子。Lee等[4]在运用MPS方法研究剧烈的自由表面振荡问题时，通过对核函数、碰撞模型、源项以及梯度模型依次修正，达到了改进判断自由表面粒子的目的，并且减少了CPU的计算时间。本文针对MPS方法中自由表面粒子判定不准确问题，开发了一种融合体积法和几何法的自由表面粒子识别方法，并且对典型的溃坝问题进行了数值模拟，进而有效地改善了MPS方法中自由表面粒子的识别。

2 数值计算方法

2.1 控制方程

对于不可压缩流体，其连续性方程和Navier-Stokes方程可表示为

(1)

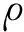
(2)

2.2 传统MPS方法

2.2.1 核函数

在MPS方法中，粒子间的相互作用关系通过核函数体现。在MPS方法中，核函数的公式如下，

(3)

式中r=|ri-rj|为两个粒子之间的距离，ri为i粒子的位置，rj为i粒子支持域内j粒子的位置，re为粒子作用域的半径，一般re=2.1l0，其中l0为初始粒子间距。

2.2.2 梯度模型

(4)

式中d为空间维度，n0为初始粒子数密度值，wi j=w(|rj-ri|)。在MPS法的模拟中，只有作为标量的压力值P参与上式计算。为了计算的稳定性，MPS方法的压力梯度计算一般为

(5)

Pj为i粒子支持域内粒子的压力，Pi min为i粒子支持域内所有粒子中压力最小的粒子压力。

2.2.3 Laplace模型

(6)

式中d为空间维度，λ定义为

(7)

λ的引入是对有限范围内的核函数代替无限范围的高斯函数带来误差的一种补偿。Laplace模型用来离散二阶导数项，在MPS法的模拟中，粘性力项用Laplace微分算子进行离散。

2.2.4 压力泊松方程

在传统的MPS方法中，压力通过求解压力泊松方程得到，其中，系数矩阵项通过Laplace模型进行离散，源项采用粒子数密度的偏差，可表示为

(8)

2.3 算法流程

MPS方法中，第一步计算重力和粘滞力作用下的速度增量，然后根据该速度增量对粒子的速度和位置进行第一次的显式修正;接下来计算此时的粒子数密度，建立并求解压力泊松方程，然后计算出第二次的速度隐式修正；最后,根据此速度隐式修正粒子最终的速度和位置。MPS方法具体的模拟流程如图1所示。

3 自由表面的判定

3.1 基于粒子数密度的自由表面识别方案

在最初的MPS方法中,流体的自由表面条件描述为，由于在自由表面以外没有流体粒子，所以在自由表面处的流体粒子数密度小于流体内部的粒子数密度，则采用式(9)来确定自由表面粒子，

(9)

3.2 改进的自由表面识别方案

分步对自由表面粒子进行筛选，首先采用几何法对自由表面粒子进行初步筛选；然后运用体积法对自由表面粒子进行进一步识别，最终达到较好的自由表面粒子识别效果。

3.2.1 几何法

(1) 基本思想

几何法的基本思想是先以一个待识别的粒子为中心，画一个直径为h的圆；然后画出以周围粒子为中心的直径为h的圆；如果这个待识别的自由表面粒子圆形未受到其周围粒子的圆形全部覆盖，则判定这个待识别的粒子为自由表面粒子。

图2中灰色的粒子是需要判定的粒子，灰色圆的直径为h；黑色的粒子是灰色粒子的周围粒子，黑色圆形的半径为h。假如以黑色粒子为中心的圆将以灰色粒子为中心的圆全部覆盖，则灰色的粒子识别为内部粒子；假如黑色圆形未将灰色圆形全部覆盖，那么灰色的粒子判定为自由表面粒子。

(2) 实现方法

几何法中，弧长的准确计算是几何法是否能够准确判定自由表面粒子的关键。如图3所示，将待识别粒子的灰色圆心和周围粒子的黑色圆心连接，那么两点之间的距离为

(10)

式中 dx为两点在x方向上的距离，dy为两点在y方向上的距离。

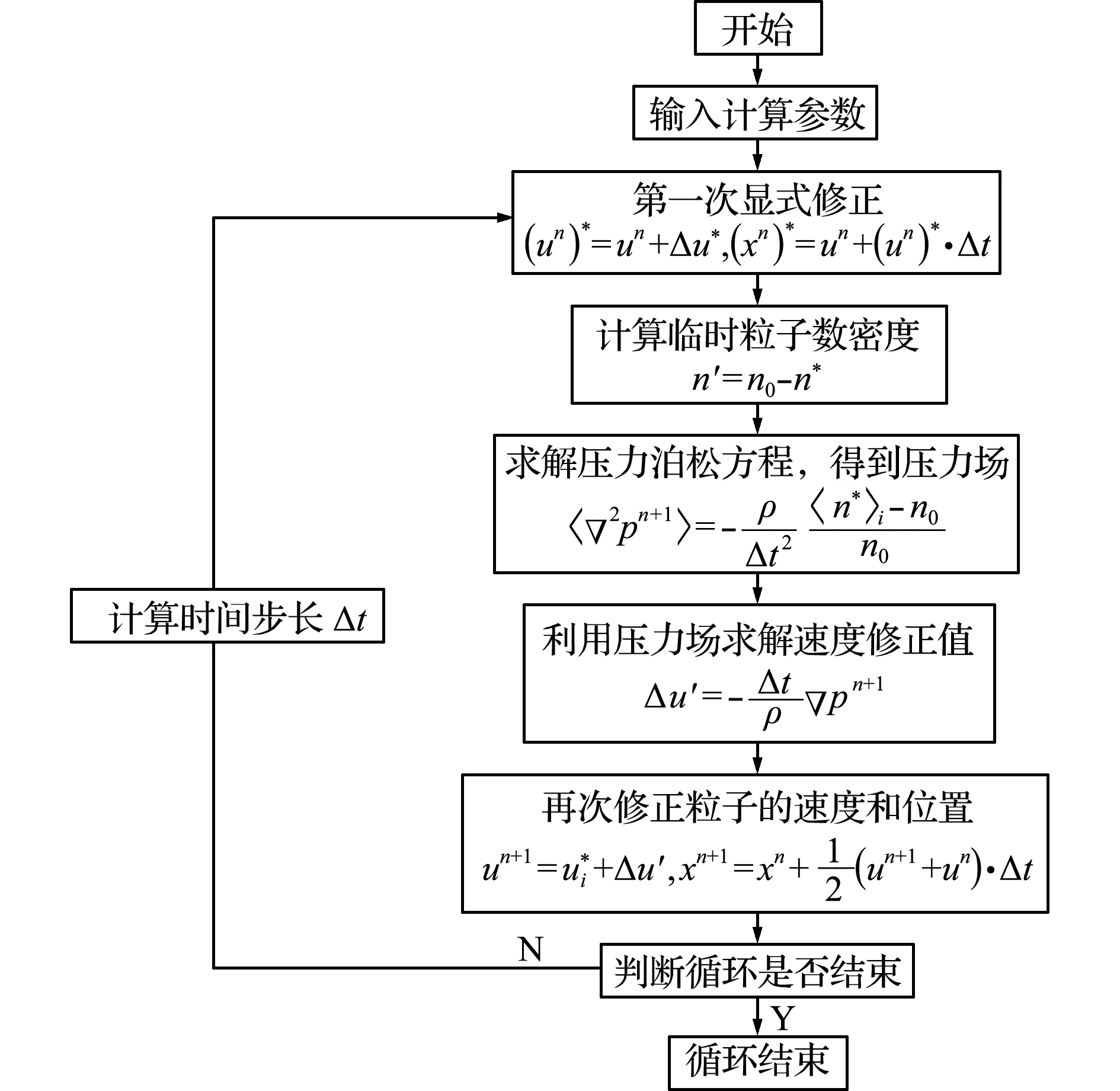
图1 MPS方法详细模拟流程

Fig.1 Simulated flow chart of MPS method

∠B=arctan(dy/dx)

(11)

两圆的圆心连线平分交点连线，如图3所示，∠A是灰色圆心与两圆交点的连接线和两圆圆心的连线所成的夹角，

∠A=arccos(dr/h)

(12)

式中h为圆的直径。图3中，圆弧的起始角∠Start和终止角∠Stop的计算如下，

∠Start=∠B-∠A

(13)

∠Stop=∠B+∠A

(14)

实际上，灰色圆心与黑色圆心的连接线所处的象限不同，起始角和终点角的计算也不同。但是其基本方法和上述情况类似，限于文章篇幅不做具体展开。

在计算出黑色圆形截取灰色圆形的每段弧的起始角和终止角后，将这些弧依次排序，然后观察其是否将灰色圆形全部覆盖。如果全部覆盖，则判定为内部粒子；否则，判定为自由表面粒子,如图5所示。

3.2.2 体积法

第一步已经判断出大部分自由表面粒子，但仍会出现个别内部粒子误判为自由表面粒子的情况。所以在第二步中，需要排除这些误判的自由表面粒子。方法如下,假如一个自由表面粒子在其支持域内的粒子都是流体粒子，则判定这个自由表面粒子为误判的自由表面粒子。如图5所示，黑色粒子识别为自由表面粒子，灰色粒子识别为流体粒子，黑色圆是黑色粒子的支持域。可以看出，在该黑色粒子的支持域内的粒子都是内部流体粒子，该黑色粒子为误判粒子。由于该粒子在流体内部，一定满足

图2 几何法判定自由表面粒子示意图

Fig.2 Surface particles detection of geometrical method

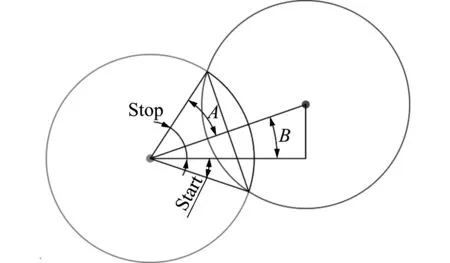
图3 几何法中弧长计算的示意图

Fig.3 Arc calculation of geometrical method

(15)

4 数值模拟结果

4.1 计算模型及参数

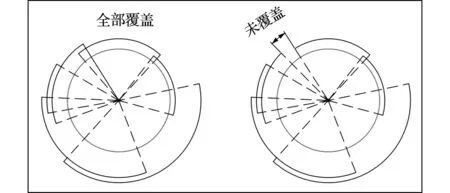
图4 几何法中所截的不同弧排序的示意图

Fig.4 Rank ordering of interceptive arc in geometrical method

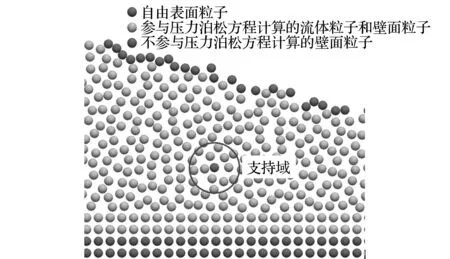
图5 几何法中误判为自由表面粒子的流体内部粒子示意图

Fig.5 Misjudgement of surface particles in geometrical method of the dam-break problem

4.2 计算结果及分析

图7是三种自由表面粒子识别方案在t=0.4 s和t=1.1 s两个时刻的自由表面粒子识别结果。此时流体流动较为平稳，三种方案计算的溃坝流型是基本一致的，但是三种方法的自由表面判别结果却有着明显的差异。在t=0.4 s时刻，采用方案1进行识别时，溃坝流体右上角处内部有一层流体误判为自由表面粒子，溃坝流体前锋处有自由表面粒子未识别的情况。这是因为采用粒子数密度大小进行判定时，在模拟过程中，会造成表面粒子以及内部粒子分布的不均匀，在粒子分布较为稀疏的地方，流体粒子的粒子数密度很可能小于判别系数β，那么此处的粒子就可能误判为自由表面粒子。然而，采用几何法自由表面粒子判定条件和采用几何法+体积法自由表面粒子判定条件进行自由表面粒子判定时，在溃坝流体右上角处的自由表面粒子都能够准确识别。在t=0.4 s时刻，采用方案2和方案3进行识别时，溃坝流体右上角处的自由表面粒子都能准确识别，在溃坝流体前锋处也都没有发生自由表面粒子未识别的情况。在t=1.1 s时刻，采用方案1进行识别时，溃坝流体靠近前锋处的流体出现了大量内部流体误判为自由表面粒子的情况，大概有20个流体内部粒子误判为自由表面粒子。采用方案2进行识别时，溃坝流体靠近前锋处的流体仍然有1个内部流体粒子误判为自由表面粒子。这是由于在流体流动过程中，粒子的流动极其复杂，在计算过程中仍然会出现几何法未考虑到的特殊情况。针对这些特例，本文又增加了一次判断，采用方案3进行自由表面粒子识别时，就能避免这种特例的发生，溃坝流体靠近前锋处再也没有出现流体内部粒子误判为自由表面粒子的情况。

表1 不同自由表面识别方案

Tab.1 Different free surface detection methods

方案1 基于粒子数密度的识别方案方案2 基于几何法的识别方案方案3 基于几何法+体积法的识别方案

图6 溃坝计算模型示意图

Fig.6 Sketch of the dam-break problem

图8是三种自由表面判定情况在t=2.45 s时刻的自由表面粒子分布示意图，此时流体撞击壁面形成了卷起的波浪，流体运动非常剧烈。针对这种情况分析三种不同的自由表面粒子识别方案的效果。从图9可以看出，当采用方案1进行判别时，由于卷起的波浪内部流体运动剧烈，导致粒子分布也非常不均匀，从而在粒子分布较稀疏处有很多流体内部粒子误判为自由表面粒子。所以方案1对流体运动剧烈情况下的自由表面粒子识别效果不是很好。采用方案2进行判别时，虽然卷起的波浪内部流体粒子分布仍然不均匀，但是几何法能够较好地克服这一问题，之前误判的大部分波浪内部流体粒子都准确地判定为自由表面粒子，说明方案2对自由表面粒子的识别效果优于方案1。但可以看出，采用方案2时，卷起波浪内部流体仍有个别粒子误判为自由表面粒子。采用方案3进行自由表面粒子判定时，所有流体内部的粒子都没有出现误判为自由表面粒子的情况，对自由表面粒子的识别效果在三种方案中最优。

4.3 计算效率的对比

图9是三种自由表面判定方案在粒子数量分别为3772,4692,8348,11228,16762和24000下的计算时间，其中CPU 计算时间是指每循环10个时间步所需的时间。可以看出，随着粒子数量的增加，三种方案的CPU计算时间都会增加。其中，采用方案1所需的计算时间最少，采用方案2所需的计算时间次之，采用方案3所花费的计算时间最多。这是因为方案1的自由表面识别最为简单，只需要对比粒子数密度；而采用方案2时，判断自由表面需要计算每个粒子受覆盖的弧长，然后进行排序，所以花费的计算时间较多；采用方案3时，不但需要计算每个粒子受覆盖的弧长且进行排序，还需要对可能误判的粒子进行进一步的排查，所以花费的计算时间最多，但是自由表面的识别效果也最好。可以看出，随着自由表面识别精度的提高，CPU计算时间也会相应增加。虽然新的几何法+体积法的自由表面识别方案在一定程度上降低了计算效率，但是降低的幅度不大。

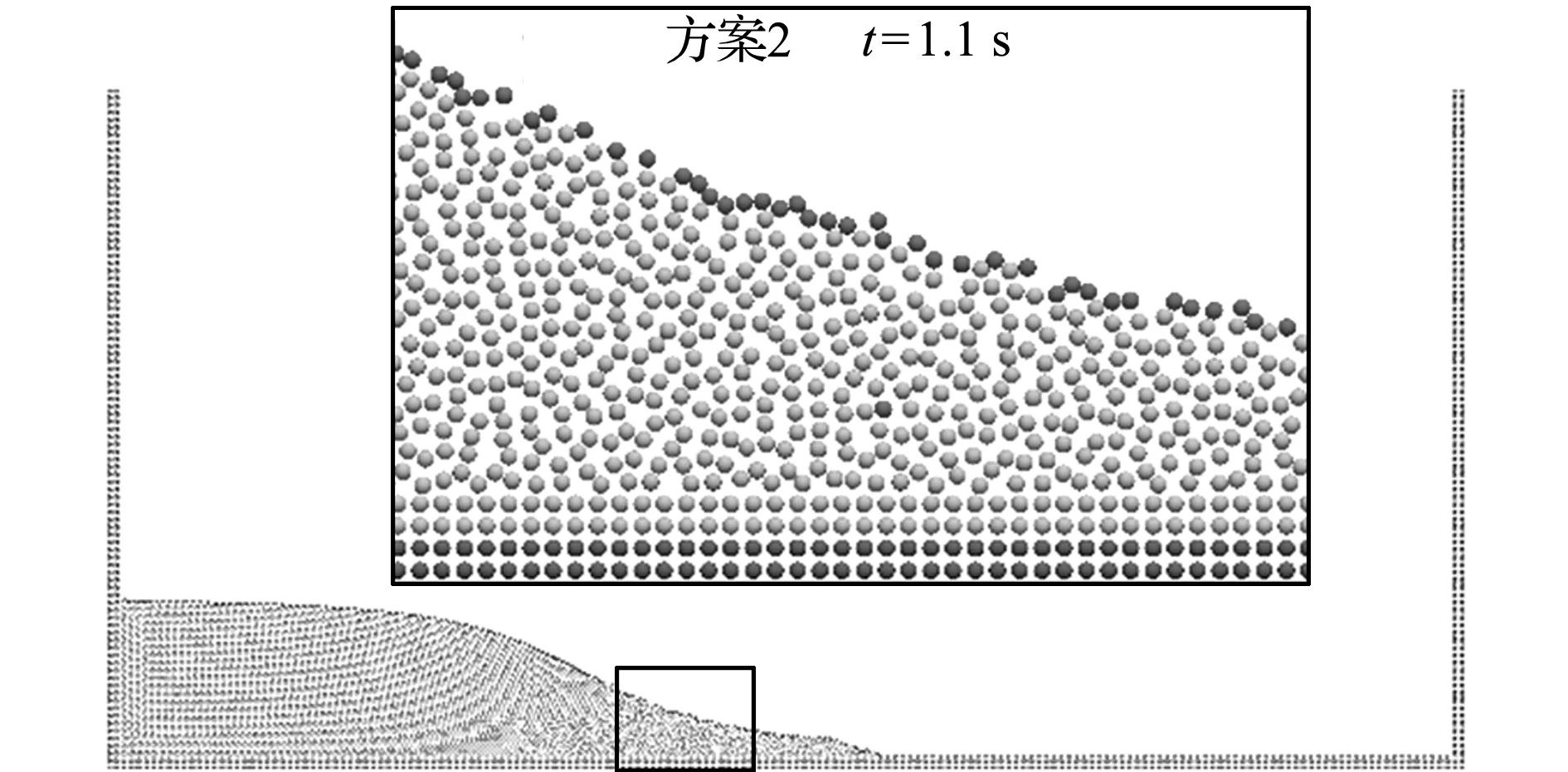
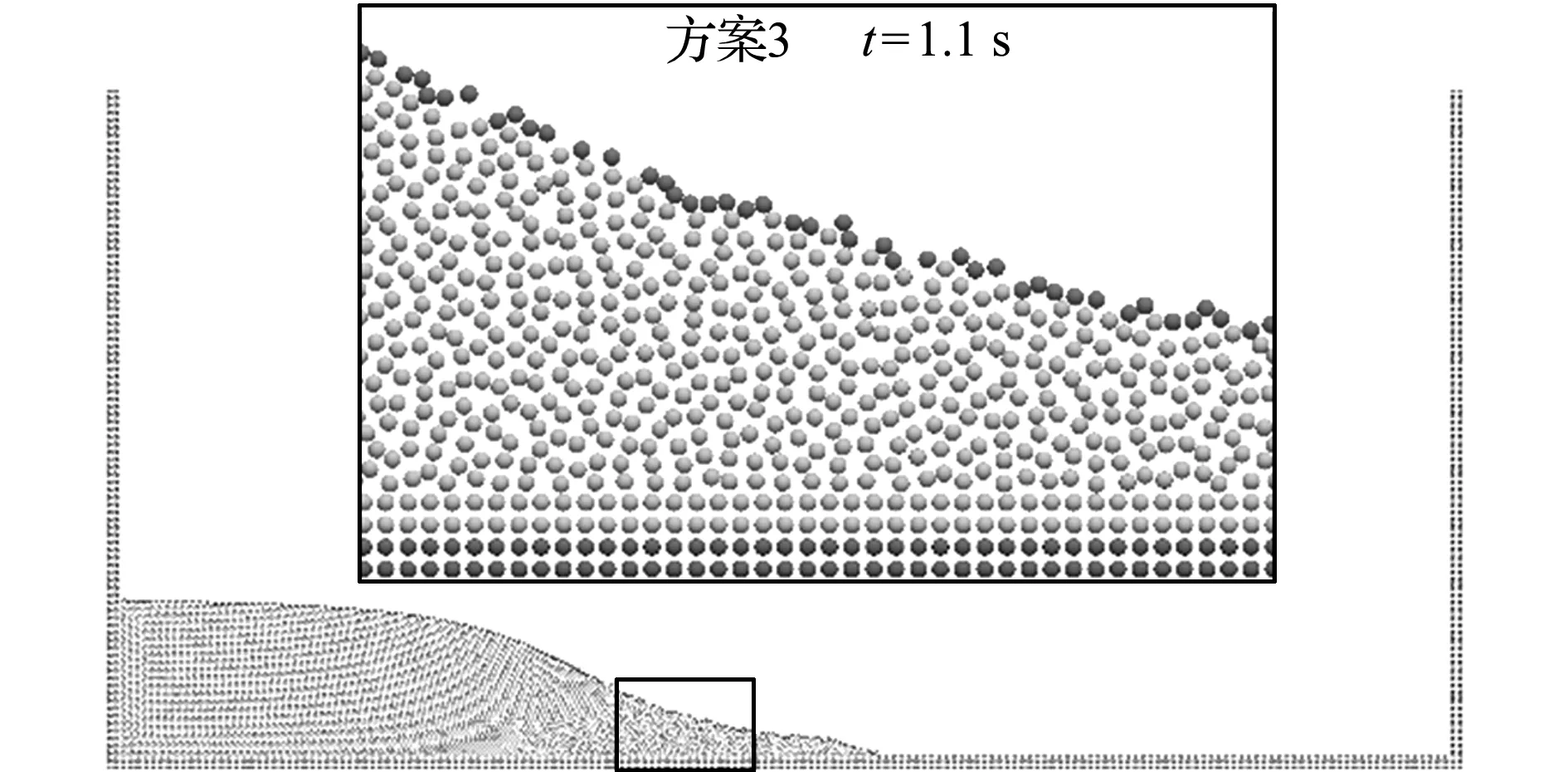
图7 三种自由表面判定情况在t=0.4 s和t=1.1 s时刻的自由表面粒子示意图

Fig.7 Detection results of three different surface particles detection methods att=0.4 s andt=1.1 s

图8 三种自由表面判定情况在t=2.15 s时刻的自由表面粒子示意图

Fig.8 Detection results of three different surface particles detection methods att=2.45 s

图9 三种自由表面识别方案在不同粒子数量下的模拟时间对比

Fig.9 Comparison of computational time between three different surface detection methods

5 结 论

本文采用MPS方法针对基于粒子数密度判定自由表面粒子效果不佳的问题，建立了两步法，包括几何法和体积法进行自由表面粒子判定的方法。采用新的两步法自由表面粒子判定方法，对溃坝模型问题进行了数值模拟。并且对溃坝流体在不同的流体运动剧烈程度下，采用不同的自由表面粒子判定方法时，比较分析自由表面粒子判定效果。结果表明，本文新建立的两步法判定自由表面粒子对于溃坝流体流动时能够准确地判断其自由表面粒子，克服了之前基于粒子数密度判定自由表面粒子的缺陷，为以后采用MPS方法研究两相流问题，不同流体之间通过界面进行传热传质问题打下了良好的基础。