四边自由各向异性矩形中厚板弯曲解析解

， ，

(西安建筑科技大学 理学院，西安 710055)

1 引 言

在各种技术和工程应用[1-3]中广泛存在各向异性板壳结构，如角点支撑的振动台、各种复合材料和航空航天用材等，在不同放置情况下都需要通过各向异性中厚板理论来解决。一般在板厚不大时，按薄板[4-9]来研究，采用直法线假设而不考虑横向剪切变形的影响。板厚较大时，根据经典薄板理论对这类结构进行分析计算就会产生较大的误差，因而要建立精化的各向异性板壳理论[10,11]。中厚板问题一直受到重视，但由于各向异性中厚板理论不但涉及非常多的弹性常数，推导过程复杂,而且由于控制方程和边界条件中偶数阶导数和奇数阶导数并存，由原来的一个控制方程变成了三个混合阶偏微分方程组，数学处理非常困难。四边自由各向异性矩形中厚板弯曲解析解未见报道。本文应用阿穆巴诸米扬理论，对不同支撑的四边自由各向异性矩形中厚板按对称性分解，并用三角级数法求得其弯曲解析解，得到的板内力更加符合实际。

2 弯曲问题及分解

2.1 平衡方程及边界条件

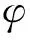
(1a)

(1b)

(1c)

式中Z2=q-F，F(x,y)为板下表面受的竖向反力，q(x,y)为板上表面受的竖向载荷。算子L13(Di k),L23(Di k)，L1,L12,L14,L2,L21和L24，函数J01,J02,J3,J4,J5和J6，常数A1,A2和A3参考文献[12]。四边自由的边界条件[12]为

x=±a/2时

Mx=0，Mx y=0，Qx=0

(2a,2b,2c)

y=±b/2时

My=0,Mx y=0,Qy=0

(3a,3b,3c)

2.2 对称性分解

w=wa a+ws s+wa s+ws a

(4a)

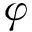
(4b)

Ψ=Ψa a+Ψs s+Ψa s+Ψs a

(4c)

q=qa a+qs s+qa s+qs a

(4d)

F=Fa a+Fs s+Fa s+Fs a

(4e)

Z2=Z2a a+Z2s s+Z2a s+Z2s a

(4f)

下标ss，aa，sa和as的含义参考文献[13]。

将平衡微分方程(1a)按对称性分解：

(5a)

(5b)

(5c)

(5d)

将平衡微分方程(1b)按对称性分解：

(6a)

(6b)

(6c)

(6d)

引入微分算子:

式中Di j,si j和Qi j参考文献[12]。

将平衡微分方程(1c)按对称性分解：

L23s a(Di k)ws a+L23a s(Di k)wa s-J4L2s sΨa a-

(7a)

L23s a(Di k)wa s+L23a s(Di k)ws a-J4L2s sΨs s-

(7b)

L23s a(Di k)wa a+L23a s(Di k)ws s-J4L2s sΨa s-

(7c)

L23s a(Di k)ws s+L23a s(Di k)wa a-J4L2s sΨs a-

(7d)

将边界条件(2a)按对称性分解：

-(D11wa a,x x+D12wa a,y y+2D16ws s,x y)+

(s44Q12+s45Q16+A1)Ψa s,y]=0

(8a)

-(D11ws s,x x+D12ws s,yy+2D16wa a,x y)+

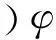
(s44Q12+s45Q16+A1)Ψs a,y]=0

(8b)

-(D11wa s,x x+D12wa s,yy+2D16ws a,xy)+

(s44Q12+s45Q16+A1)Ψa a,y]=0

(8c)

-(D11ws a,x x+D12ws a,yy+2D16wa s,xy)+

(s44Q12+s45Q16+A1)Ψs s,y]=0

(8d)

将边界条件(3a)按对称性分解：

假如“其父善游”理论成立，那么姚明的儿子，生下来就能打篮球；潘长江的儿子，一出生就会演小品；体操运动员的儿子，一出生就能接二连三地翻筋斗；杂技演员的儿子，一出娘胎就应该跳到吊灯上荡秋千。果能如此，所有的教育机构都应该关门大吉，只需各种“善游之父”多多生儿育女，就可以源源不断地为社会供给人才。

-(D12wa a,x x+D22wa a,y y+2D26ws s,x y)+

(s44Q22+s45Q26+A2)Ψa s,y]=0

(9a)

-(D12ws s,x x+D22ws s,y y+2D26wa a,x y)+

(s44Q22+s45Q26+A2)Ψs a,y]=0

(9b)

-(D12wa s,x x+D22wa s,y y+2D26ws a,x y)+

(s44Q22+s45Q26+A2)Ψa a,y]=0

(9c)

-(D12ws a,x x+D22ws a,y y+2D26wa s,x y)+

(s44Q22+s45Q26+A2)Ψs s,y]=0

(9d)

边界条件(2b)和(3b)形式相同，将其按对称性分解为

-(D16wa a,x x+D26wa a,y y+2D66ws s,x y)+

(s44Q26+s45Q66+A3)Ψa s,y]=0

(10a)

-(D16ws s,x x+D26ws s,y y+2D66wa a,x y)+

(s44Q26+s45Q66+A3)Ψs a,y]=0

(10b)

-(D16wa s,x x+D26wa s,y y+2D66ws a,x y)+

(s44Q26+s45Q66+A3)Ψa a,y]=0

(10c)

-(D16ws a,x x+D26ws a,y y+2D66wa s,x y)+

(s44Q26+s45Q66+A3)Ψs s,y]=0

(10d)

将边界条件(2c)和(3c)按对称性分解为

(11a，11b)

(11c,11d)

J6Ψa a=0，J6Ψs s=0

(12a，12b)

J6Ψa s=0，J6Ψs a=0

(12c，12d)

由方程(5a,5b,6c,6d,7c,7d)与边界条件 (8a,8b，9a,9b，10a,10b)和(11c,11d,12c,12d)构成的问题称为中心对称问题;由方程(5c,5d,6a,6b,7a,7b)与边界条件(8a,8b,9a,9b,10a,10b)和(11a,11b,12a,12b)构成的问题称为中心反对称问题。显然该问题可分解为中心对称问题和中心反对称问题的叠加。

3 方程求解

3.1 中心对称问题求解

为了满足边界条件及求导方便[14]，设

wa a(a/2,y)=∑ansinβny

wa a,x x(a/2,y)=∑bnsinβny

ws s, x(a/2,y)=∑cncosβny

Ψa s(a/2,y)=∑gncosβny

Ψs a, x(a/2,y)=∑hnsinβny

wa a(x,b/2)=∑Amsinαnx

wa a,y y(x,b/2)=∑Bmsinαnx

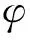
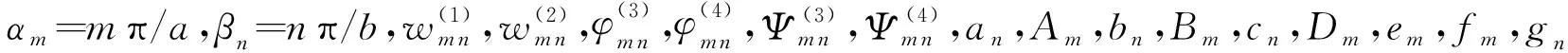
3.1.1 荷载展式

设对称荷载和反对称荷载分别为qs s和qa a，则

3.1.2 地基或支承反力展式

(1) 对地基板，若对称的地基反力和反对称的地基反力分别为Fs s和Fa a，则

(2) 对点支撑板，支反力Fs s和Fa a为

式中i=1,2,3，…,I为支撑点编号,(xi,yi)为支撑点的坐标,F(i)为第i支撑点处的支撑反力值。

3.1.3 定解方程的建立

(1) 对地基板，地基表面的竖向位移与板的挠度相等，参考文献[13]得到变形协调方程。

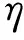
(2) 对点支撑板，在支承点坐标(xi,yi)处挠度为0，得到变形协调方程：

3.2 中心反对称问题求解

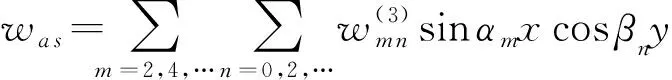
wa s(a/2,y)=∑cncosβny

wa s，x x(a/2,y)=∑dncosβny

ws a, x(a/2,y)=∑ansinβny

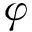
Ψa a(a/2,y)=∑fnsinβny

wa s,y(x,b/2)=∑Cmsinαmx

ws a(x,b/2)=∑Amcosαmx

ws a,y y(x,b/2)=∑Bmcosαmx

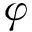
Ψs s,y(x,b/2)=∑gmcosαmx

3.2.1 荷载展式

设关于x对称，y反对称的荷载为qa s，关于x反对称，y对称的荷载为qs a，则

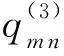
3.2.2 地基或支承反力展式

(1) 对地基板，若关于x对称，y反对称和关于x反对称，y对称的地基反力分别为Fa s和Fs a，则

(2) 对点支撑板，支反力Fa s和Fs a分别为

3.2.3 变形协调方程

对地基板及点支撑板，分别为

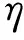
同中心对称问题类似，可求出wa s和ws a。

4 算例分析

算例1考虑文献[15]的算例2，结果列入表1。由表1可知,板中心挠度值和弯矩值与文献[15]结果接近,说明本文求解方法可行。

算例2边长为1的四边自由方薄板受8个对称的点支撑[14]。在板中心(0,0)作用单位集中力，无量纲化后求得挠度最大值wmax为0.01632,与文献[14]的0.016548基本一致。

算例3分析一长为4 m，厚为0.2 m的四边自由方形地基板的弯曲。取板物性参数如下，D11=107，EL/ET=40，EL/EZ=20，GLT/ET=0.5，θ=π/4，μL T=0.25，μL Z=0.167，μT Z=0.167，其中EL，ET和EZ分别为复合材料三个主方向的弹性模量,GL T为面内剪切模量，θ为EL对应的主方向和x轴的夹角。地基参数中，泊松比均为0.25，水平和竖向变形模量分别为40 MPa和 60 MPa，竖向平面内的剪切模量为30 MPa。板受均布荷载q=0.98 MPa作用。

表1 板中心挠度和弯矩

Tab.1 Deflection and moment of at

the plate center

板厚h/m本文理论文献[15]Wmax/mMx/kNWmax/mMx/kN1.00.0541406.180.0541409.38

图1 弯矩Mx

Fig.1 MomentMx

图2 弯矩Mx

Fig.2 MomentMx

所得弯矩如图1所示。将EZ,μL Z和μTZ取为0时，所得弯矩如图2所示。可以看出，对各向异性中厚板，载荷对称但是板的弯矩却不对称，厚度方向弹性参数对弯矩影响也较为明显。

5 结 论

(1) 本文应用阿穆巴诸米扬理论，对不同支撑下四边自由各向异性矩形中的厚板弯曲问题，按对称性分解并用三角级数法求得问题的解析解。取消了直法线假设，去除了数值法的弊端，分析得到板的挠度及内力更符合实际情况。而且能进一步分析各向异性及不同支撑条件对板弯曲特性的影响。

(2) 本文的求解方法和技术可用于求解各向异性矩形中厚板的自由振动问题和稳态振动问题。

(3) 本文方法还可分析不同边界约束下各向异性矩形中厚板的弯曲和振动问题。