核主泵叶轮间隙的轴向振动特性研究

， ， *

(1.大连理工大学 工程力学系 工业装备结构分析国家重点实验室,大连 116024;2.大连理工大学 能源与动力学院,大连 116024)

1 引 言

核主泵叶轮是核主泵的核心旋转部件，其动力特性关系核主泵的安全运行。介于泵壳和叶轮之间的叶轮口环间隙会使核主泵产生容积损失，改变叶轮内部的流场，同时也对核主泵的整体性能以及轴向力和径向力均产生重要影响。因此对核主泵口环间隙的动力特性进行研究，以及分析间隙的动力特性对结构整体性能的影响是十分必要的[1]。

间隙流问题广泛存在于工程领域,如平衡装置(轴承)、密封装置和涡流泵口环等具有狭长流道的结构。由于流致振动导致工程事故频发，间隙流致振动问题已得到广泛的重视[2-4]。随着转子转动高速化和工作环境复杂化，诱导间隙流致振动的因素逐渐增多[5,6]。

各国研究人员已对间隙流致振动问题展开了大量的研究工作[7-16]。Inada等[7-9]研究了一维间隙流道上壁面周期运动时的壁面流体力特性以及流体等效刚度、阻尼和质量特性。Li等[10]对环型间隙流道的动力特性进行了研究，环形构件处于流道中，具有垂直于流道的振动并且关于主轴旋转。通过理论研究得到了环形移动壁面下的流体力和流体动力特性。 Childs等[11,12]分别使用数值模拟和实验方法研究了泵外壳和叶轮的相互作用，分析了前盖板和壳体的间隙以及环形密封间隙的动力特性对结构整体流致振动的影响。Childs[13]使用BULK FLOW理论对单级双吸泵口环间隙进行了轴向振动特性分析，指出单级双吸泵在固有频率低于旋转速度10%的情况下，轴向力才会对结构产生重要影响。Horiguchi等[14]对具有径向流动的推力轴承间隙进行了轴向振动实验研究和数值模拟，发现扩大流道会引起负刚度或负阻尼，造成止推轴承轴向失稳。Sugiyama等[15]建立了狭窄间隙的理论模型，对径向间隙流引起的轴向自激振动进行了理论分析。

现有研究成果多基于不同间隙流介质以及相关理论模型得到，水介质环境下考虑真实核泵间隙边界条件的径向间隙流对轴向振动特性的研究并不多。另外，根据核主泵转子轴向振动引起的止推轴承失效事故可以发现[1]，旋转间隙流对核主泵转子起到轴向支撑作用，其动力学特性对转子轴向振动的稳定性具有重要意义。因此，需要对真实核泵叶轮间隙动力特性进行深入研究。

本文针对径向间隙流致振动展开了三方面研究。首先，建立有径向间隙的理论分析模型，使用文献[14]的计算条件(介质为空气)进行数值计算并与之对比，验证本文复杂边界下间隙流的数值结果及分析方法的正确性。其次，考虑核泵叶轮间隙介质为水的情况，分析对比不同流体介质(空气和水)对轴向动力特性的影响。分析发现介质为水时，径向间隙流可引起间隙产生负轴向动力因子，进而研究在流体介质为水时流道形状对轴向动力特性的影响。最后，使用理论模型中的计算方法，对核主泵原型叶轮与泵壳间隙模型的轴向特性进行分析，研究其轴向振动特性，并对核主泵原型叶轮间隙做出评估。对比不同间隙大小的核主泵间隙模型，分析间隙大小对模型轴向特性的影响。这些结果为核主泵叶轮间隙的设计和安全运行提供了评估依据。

2 理论间隙模型及计算方法验证

由于核泵叶轮间隙有复杂的动边界以及工程流体复杂性，为确保数值计算可靠，本文首先对理想化的圆环流道模型进行轴向振动特性理论研究，并与文献[14]的结果进行比较，对计算结果进行验证，确定计算方法的可行性。

2.1 理论间隙模型

间隙结构的简化几何模型如图1所示。间隙由两个圆环壁面组成，两圆环壁面中间有流体介质流过。模型的下壁面为固定圆环面，上壁面为圆环面，该面绕轴转动并且伴随轴向振动；中间部分为流道间隙，流体从圆环内径流向圆环外径(外流)或由圆环外径流向圆环内径(内流)。

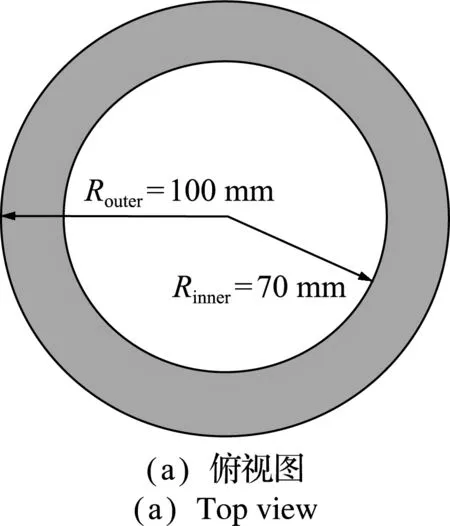
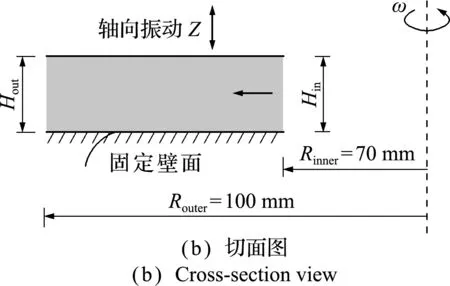
图1 径向间隙流模型(Hin和Hout分别为入口和出口宽度)

Fig.1 Model of the radial clearance(HinandHoutare the width of the inlet and outlet respectively)

根据间隙几何模型尺寸，建立Fluent计算模型，如图2所示。模型网格总数为720000，采用8节点六面体网格。考虑几何模型的径向、周向和轴向尺寸的比例和网格的合理性，径向、周向和轴向的网格节点数分别设置为60,600和20。以上网格划分方式基于网格无关性验证结果。

2.2 轴向刚度和阻尼因子求解

通过数值仿真，可求得移动壁面上的轴向流体力，随后可求得间隙的等效轴向刚度和阻尼，进而对间隙的轴向振动特性进行分析。通常轴向振动因子可由以下方法求得。

移动壁面上的流体力F可表示为[14]

(1)

式中K为等效刚度，C为等效阻尼，Z为移动壁面的位移。

任意两个时刻t1和t2的轴向力Ft 1和Ft 2可表示为

(2，3)

由式(2，3)求解得到等效刚度和等效阻尼的表达式为

(4)

其中，移动壁面Z方向的作用力响应Ft 1和Ft 2可由数值计算求得。因此轴向刚度和阻尼特性因子可由式(4)求得。

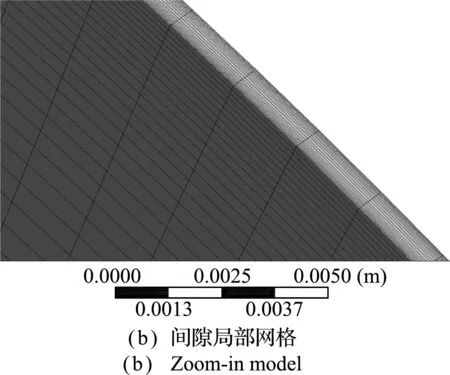
图2 平行流道计算网格

Fig.2 Finite element model of the flat clearance

2.3 数值结果对比

由于文献[14]的流体介质为空气，因此本节数值计算使用的流体介质为理想空气。其他计算条件与文献[14]保持一致，环境压力为一个标准大气压，温度为293 K，入口质量流量为0.0059 kg/s，出口压力为0 Pa，下壁面速度为0 m/s，上壁面绕Z轴旋转，转速ω=1200 r/min。同时，上壁面做轴向简谐运动，运动方程由式(5)给出，振幅为0.2 mm。

Z为移动壁面的位移，

(5)

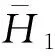
通过数值计算可获得壁面轴向力。以轴向振动频率为20 Hz的结果为例。轴向振动频率为20 Hz时，壁面轴向力的标准时域结果和频域分析结果分别如图3(a，b)所示。 可以看出，图3(b)包含了振动基频、二次和三次谐波频率。谐波的出现可由系统的非线性和网格离散等因素引起。因为谐波分量相对基频幅值较小，为方便后续线性动力学分析，故对轴向力数据进行滤波处理，保留振动基频。 处理后数据的时域和频域结果如图3(c，d)所示。

滤波处理后的壁面轴向流体力可在式(4)中对等效轴向刚度和阻尼进行求解。利用式(6,7)对等效轴向刚度和阻尼进行无量纲处理。

(6,7)

图4给出了在轴向频率分别为0.5ω，1ω，1.5ω，2ω，2.5ω和3ω情况下，四种湍流模型的计算结果与文献数据的对比结果。图4中同一个湍流模型结果上的数据点，沿虚线箭头方向，从下到上分别对应是轴向频率从0.5ω～3ω的结果。

可以看出,(1) 随着轴向振动频率的增加，四种湍流模型的计算结果趋势与文献[14]结果趋势基本一致，即随着轴向振动频率增加，轴向刚度不断减小，轴向阻尼不断增大；(2) 四种模型的无量纲阻尼计算结果均与文献结果吻合较好；(3) 采用Realizablek-ε模型计算时，无量纲轴向刚度因子与文献[14]结果吻合较好；(4) 由于Realizablek-ε模型对有旋转均匀剪切流、自由流(射流和混合层)和腔道流动的计算精度更高[17],因此Realizablek-ε模型更适合模拟本文所研究的间隙流问题。

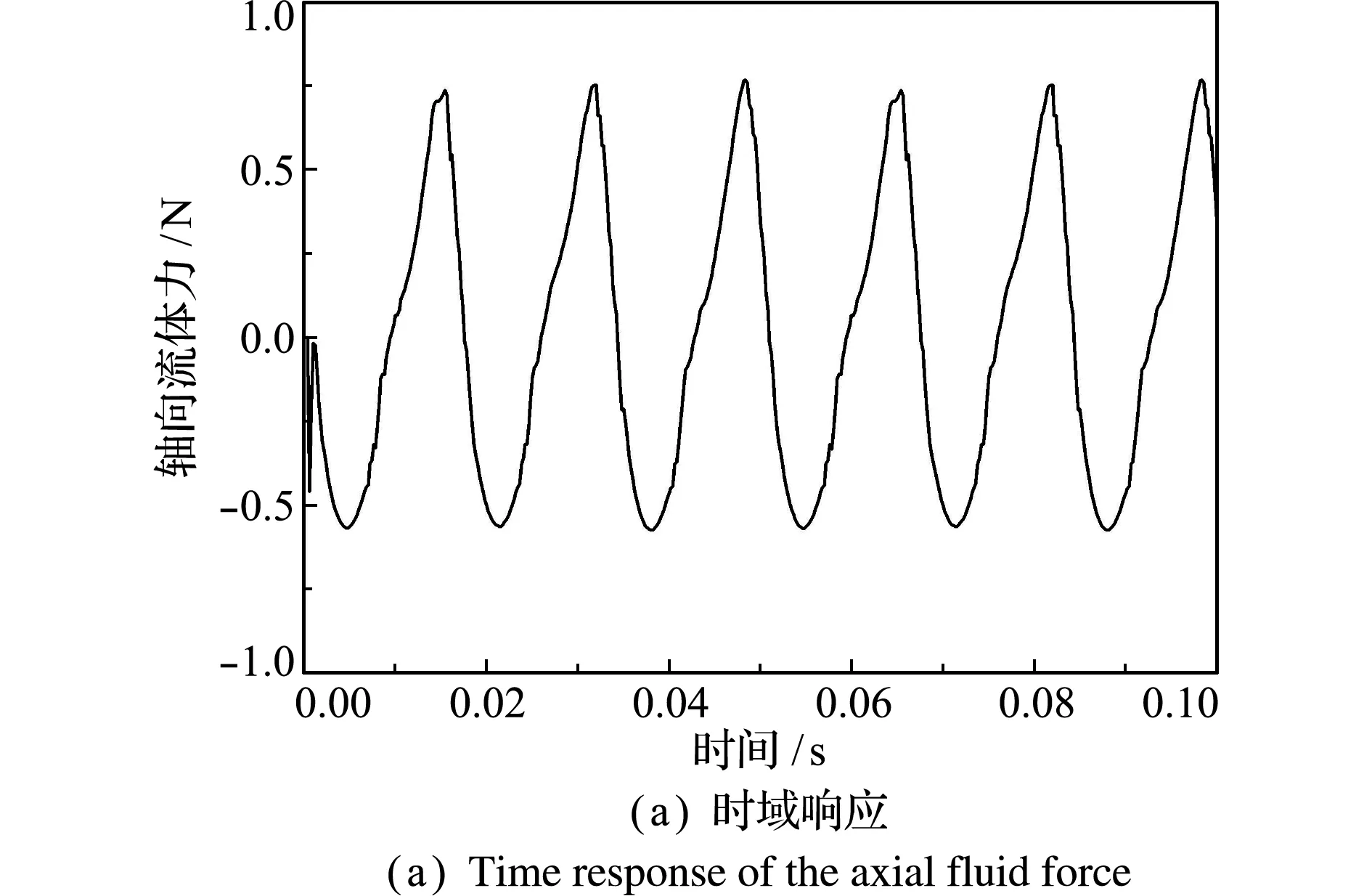
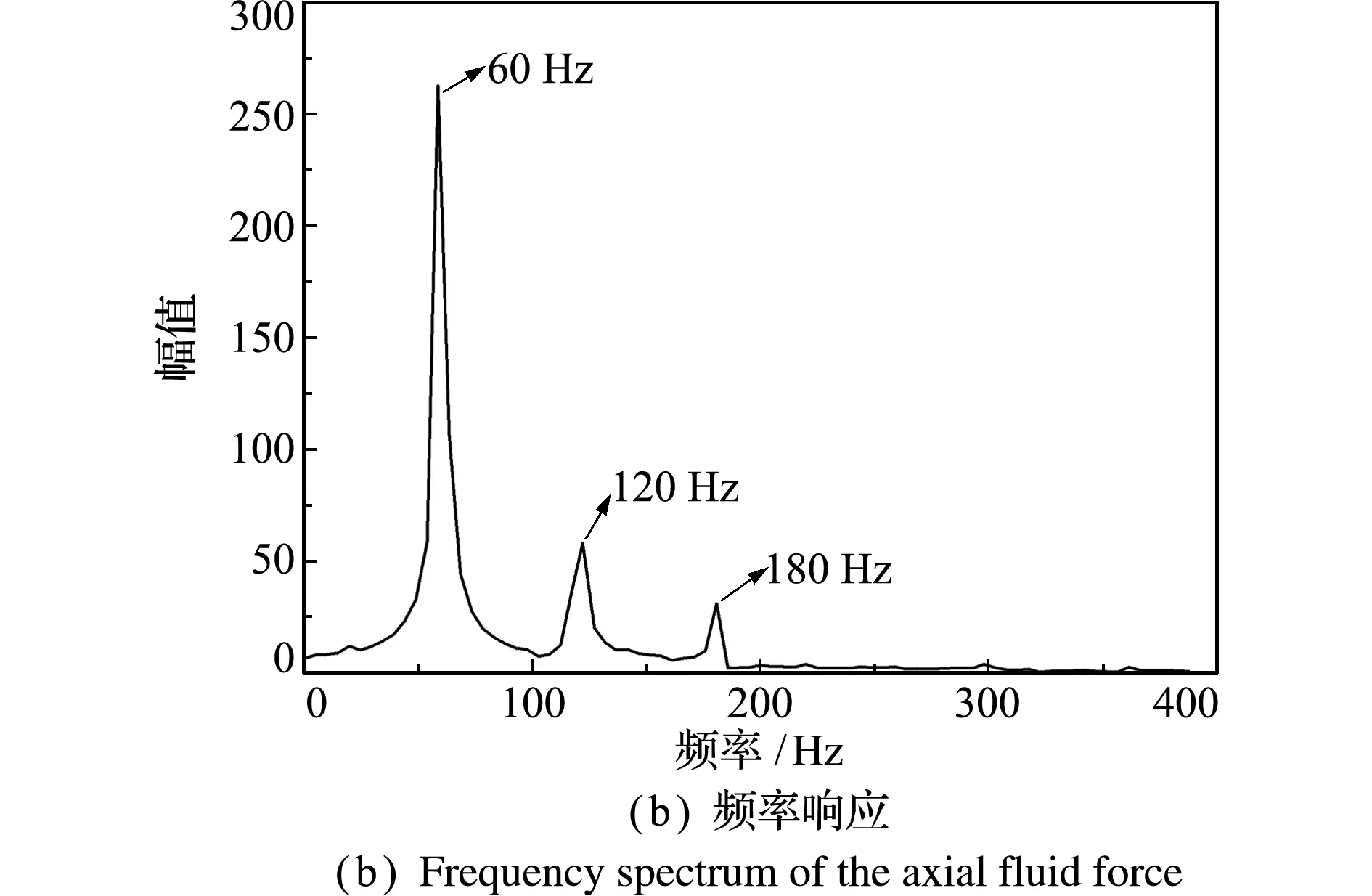
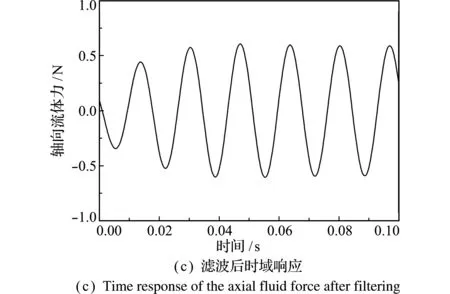
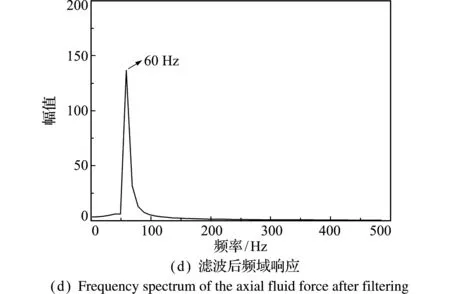
图3 滤波前后上壁面所受轴向流体力响应

Fig.3 Results of the responses of the axial fluid force acting on the upper wall of the clearance before and after filtering

3 理论间隙模型的轴向动力分析

3.1 不同流体介质对振动特性的影响

为了与文献[14]的结果进行对比，第2节使用的流体介质为空气。而真实的核泵内流体介质为水，其密度和粘性动力系数与空气差别较大，因此对介质为水时的理论间隙模型的轴向动力特性进行研究。

图5是流体介质为水和空气时的轴向振动因子随轴向振动频率的变化规律。结果表明，(1) 当流体介质为水和空气时，无量纲刚度和阻尼因子随轴向振动频率变化的趋势一致，即刚度随轴向振动频率的增大而减小，阻尼随振动频率的增大而增大；(2) 流体介质不仅会对轴向刚度和阻尼数值产生影响，并且会改变轴向动力性质；(3) 当介质为水时，轴向刚度为负值，可能对结构振动产生不利影响。因此，即使是简单的理论模型，其介质特性对轴向振动特性的影响也非常明显。

3.2 不同流道形状对轴向特性的影响

由于流体介质为水时，间隙轴向等效刚度可能为负值，因此研究流道形状对轴向动力因子的影响。不同的流道形状如图6所示。

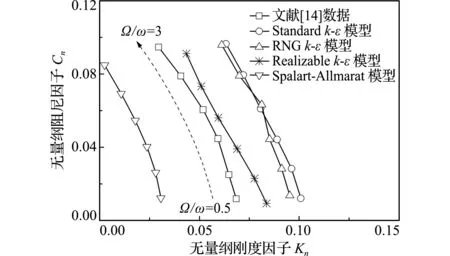
图4 不同湍流模型数值结果与文献结果对比

Fig.4 Comparisons between the numerical results and those in Ref.[14],calculated through different turbulence models

图5 不同介质轴向动力特性

Fig.5 Dynamic behavior in the axial direction of different fluid medias

采用叶轮口环真实压力作为边界条件,Pin=17.88 MPa，Pout=17.1 MPa。高温高压水的密度为602.6 kg/m3，动力粘性系数为7.603×10-5N·s/m。通过对三种流道形状中流体的外流和内流六种类型间隙进行数值计算和动力分析，轴向刚度随轴向振动频率增大的变化如图7所示，轴向阻尼随轴向振动频率的变化如图8所示。

从图7和图8可以看出，(1) 当平行流道为外流(流体方向为从内径流向外径)，扩张流道为内流(流体方向为从外径流向内径)和外流时，轴向刚度均为负值，数量级为106，将会改变整体结构的振动频率，同时有可能引起振动不稳定；(2) 值得注意的是，平行流道和扩张流道外流时，轴向阻尼会产生负值，引起系统振动不稳定；(3) 不同轴向振动频率下，三种流道的轴向振动因子变化规律不完全一致。扩张流道外流时的阻尼随轴向振动频率的增大而增大，而平行流道外流时阻尼随轴向振动频率的增大而减小，并由正变为负。因此，当间隙流道为收缩流道时，轴向刚度和阻尼均为正值，最为稳定；当为平行和扩张流道时，轴向阻尼为负值，会造成系统不稳定。所以收缩流道相对安全。

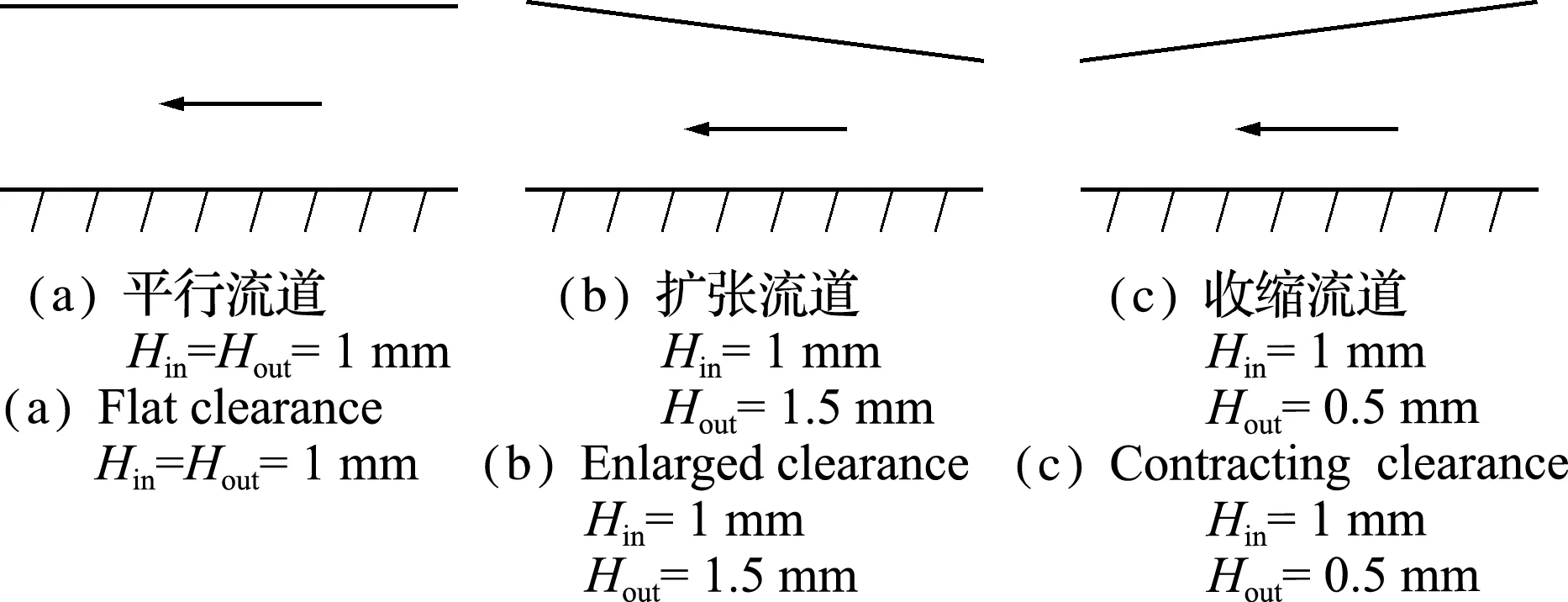
图6 三种流道形状

Fig.6 Three kinds of clearances

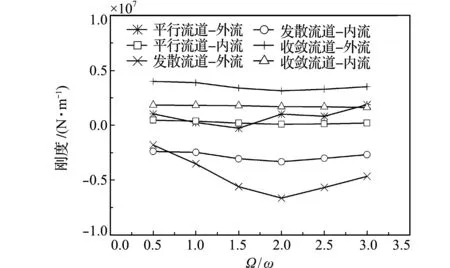
图7 不同振动频率下轴向刚度的变化规律

Fig.7 Change of the axial stiffness withΩ/ω

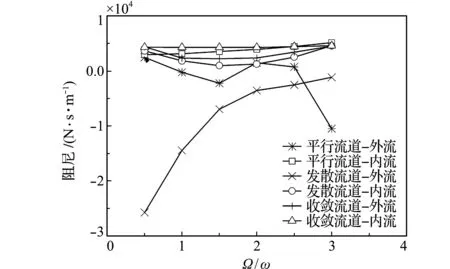
图8 不同振动频率下轴向阻尼的变化规律

Fig.8 Change of the axial damping withΩ/ω

4 核主泵模型数值计算

4.1 核主泵原型叶轮间隙几何模型

AP1000核主泵原型叶轮间隙模型如图9所示，入口间隙和出口间隙尺寸均为8.314 mm，入口处半径为0.6945 m。流体由叶轮末端A流入，流经叶轮间隙，由核泵吸入口间隙B流出。由于核主泵在运行中产生轴向振动，因此模型内侧壁面C有轴向的周期运动。

4.2 模型单元敏感性分析及周期边界条件验证

从图9可以看出，叶轮间隙模型具有复杂的动边界,因此六面体单元不再适用,采用更广泛适用于动网格计算的四面体单元对核泵叶轮间隙进行数值计算，以满足动网格要求。

由于网格的敏感性，需对四面体单元的计算结果(图1间隙)与之前的六面体单元计算结果进行对比验证，确定四面体单元计算结果可靠性。但使用四面体单元对叶轮间隙的整个模型进行网格划分来满足单元质量要求，网格数量将超过1000万，计算量庞大。

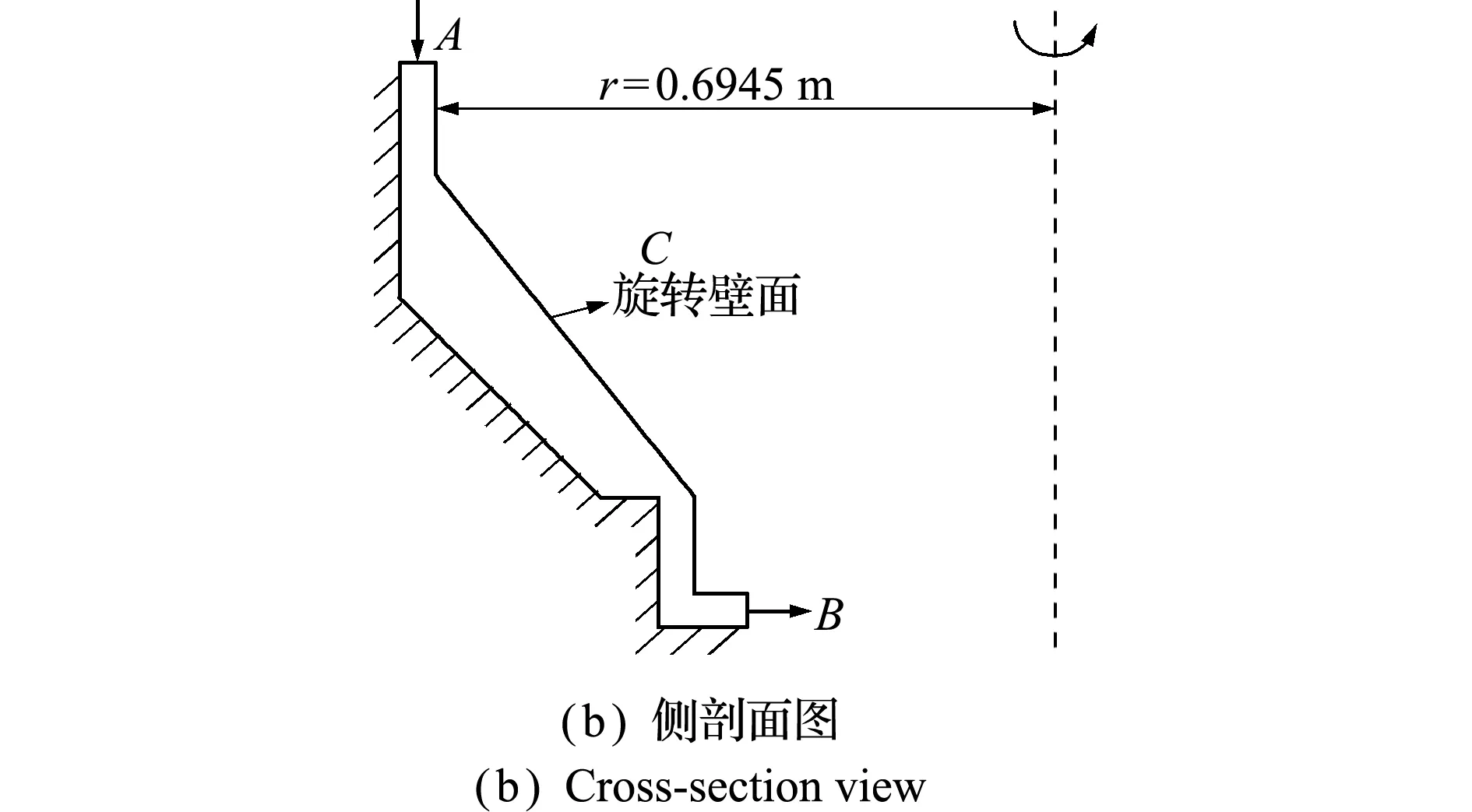
图9 核主泵原型叶轮间隙模型

Fig.9 Model of the impeller clearance

由第3节可知，六面体单元的计算结果精度高。为确保对比一致性，首先对具有循环对称边界并且由六面体划分的1/12间隙模型进行计算，并与相应的完整间隙模型计算结果进行对比。限于篇幅,表1给出其中一组使用六面体网格的对比结果。可以看出，使用旋转周期边界的计算结果与完整模型的计算结果基本一致，误差在允许范围内，因此，确定了使用循环对称边界对间隙模型进行简化的可行性。随后分别使用四面体和六面体网格对此1/12间隙模型进行划分，并验证确定四面体单元计算结果的准确性。对比结果列入表2。 由表2可知，使用四面体单元对模型进行网格划分的计算结果和六面体单元划分方法的计算结果基本一致，误差在容许范围内。因此，可使用四面体单元对间隙流振动类问题的实体模型进行网格划分。

基于以上验证，以下核主泵原型模型将采用具有循环边界条件的1/12核泵间隙模型和四面体单元进行数值计算。

4.3 核主泵原型叶轮间隙模型的数值模拟

4.3.1 1/12 AP1000间隙计算模型及计算条件

基于4.2节的验证，1/12的核泵间隙模型如图 10所示，网格采用四面体单元，边界层网格为楔形体。网格尺寸为0.002 m，边界首层大小为1.5×10-4m，边界层增长率为1.2，边界层层数为4，有限元模型网格数量为3688144。此模型同样也通过了网格的无关性验证。使用此模型对核主泵原型叶轮间隙的动力特性进行研究。

表1 周期边界验证结果

Tab.1 Validation on the results with periodical boundary

流道类型完整间隙模型1/12间隙模型刚度阻尼刚度阻尼刚度误差/%阻尼误差/%contract-outward35260614479.8335410064700.210.424.92

表2 不同单元对比结果

Tab.2 Comparison between the results with different type of the element

流道类型六面体单元模型四面体单元模型刚度阻尼刚度阻尼刚度误差/%阻尼误差/%contract-outward35410064700.2138368405105.278.358.62

4.3.2 基于不同轴向振动幅值的计算结果

根据轴向振动幅值对轴向动力特性的影响，分别采用0.1 mm和1 mm轴向振动幅值进行计算。0.1 mm为核主泵运转时轴向振动幅值。 1 mm 考虑的是在危险情况下的工况，虽然振动表现出非线性，但基频仍占主导地位，所以与2.3节的小振幅工况一样，忽略非线性影响。 计算结果列入表3，可以看出，(1) 核主泵叶轮间隙在两种振动幅值下都表现出负轴向刚度，数量级为107。 (2) 两种不同轴向振动幅值下，间隙轴向阻尼特性改变。当轴向振动幅值为0.1 mm时，轴向阻尼为负阻尼，数量级为105；当轴向振动幅值为1 mm时，轴向阻尼为正值，对系统起稳定作用。核主泵叶轮间隙在该运转条件下，表现出的负阻尼和负刚度特性将会引起结构的不稳定。考虑核主泵整体结构的刚度数量级为 109，负刚度将降低振动频率。因而负阻尼所造成的发散振动将会对结构产生严重影响。

4.3.3 叶轮间隙尺寸对动力特性的影响

相对于图10，图11所示模型的叶轮流道间隙较小。由于图10的流道间隙模型(原始模型)会引起结构的不稳定，因此对图11的修改模型进行分析，研究对比不同流道形状对间隙特性的影响。边界层划分与网格划分方法与原始模型保持一致，流道计算模型如图11(b)所示，网格数量为1748590。

在轴向振动幅值为1 mm时，两种模型叶轮间隙总动力特性结果列入表4，可以看出，两个模型的轴向刚度都为负，数量级相当，均可能造成系统的不稳定，并且轴向阻尼均为正值。当流道局部间隙减小时，轴向负刚度增加26%。轴向正阻尼增加66%，提高了系统的稳定性。

表3 不同振动幅值下的动力系数

Tab.3 Dynamic coefficients under different amplitudes of the external excitations

轴向振动幅值轴向刚度 轴向阻尼 0.1 mm-36204982-545411 1 mm-2407553937230

表4 不同间隙形状计算结果

Tab.4 Results of different kinds of clearance

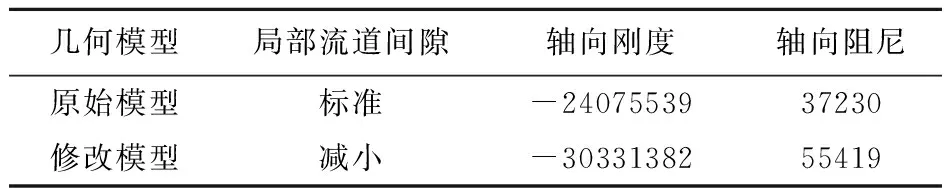
几何模型局部流道间隙轴向刚度轴向阻尼原始模型标准-2407553937230修改模型减小-3033138255419

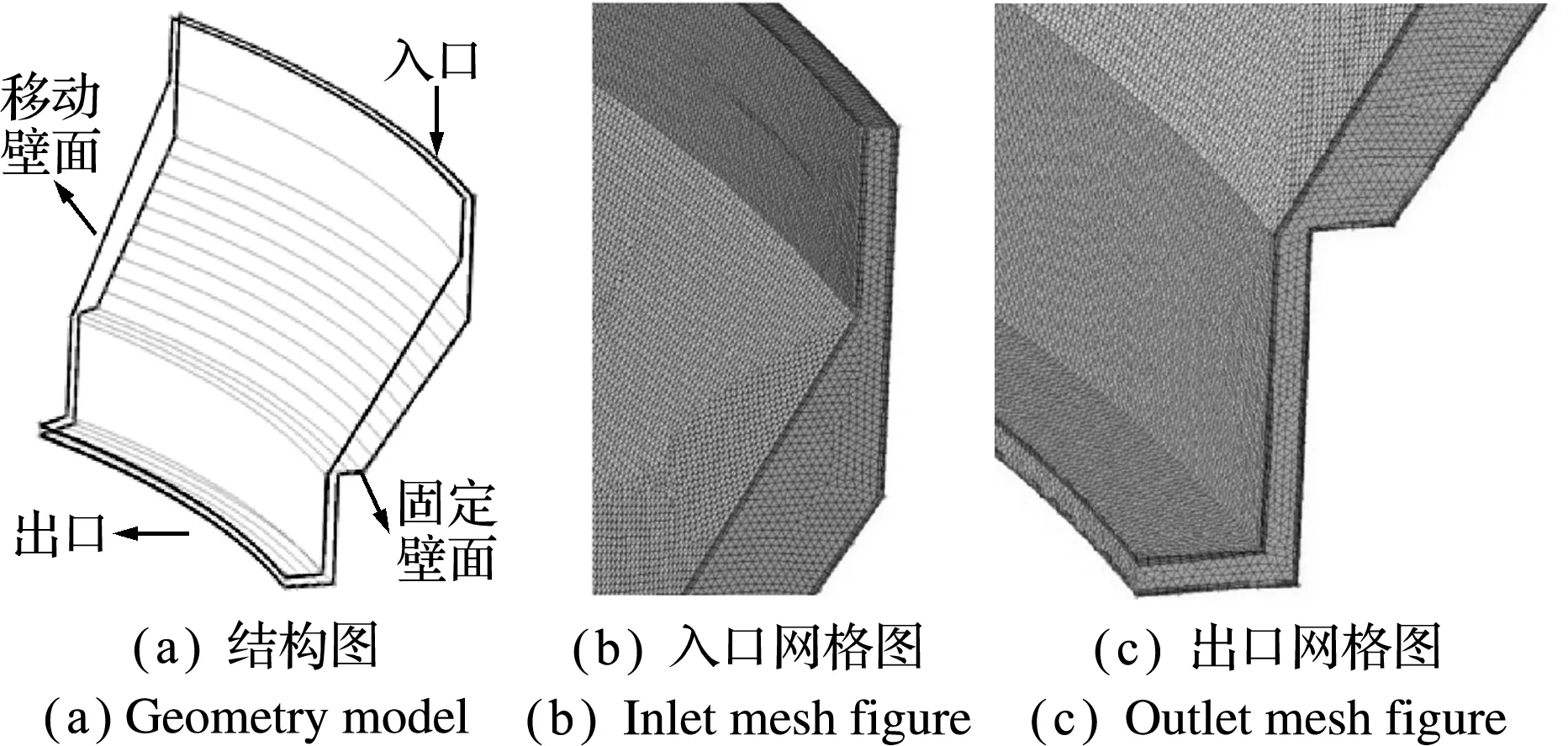
图10 1/12核泵间隙几何及计算模型

Fig.10 1/12 of the pump clearance

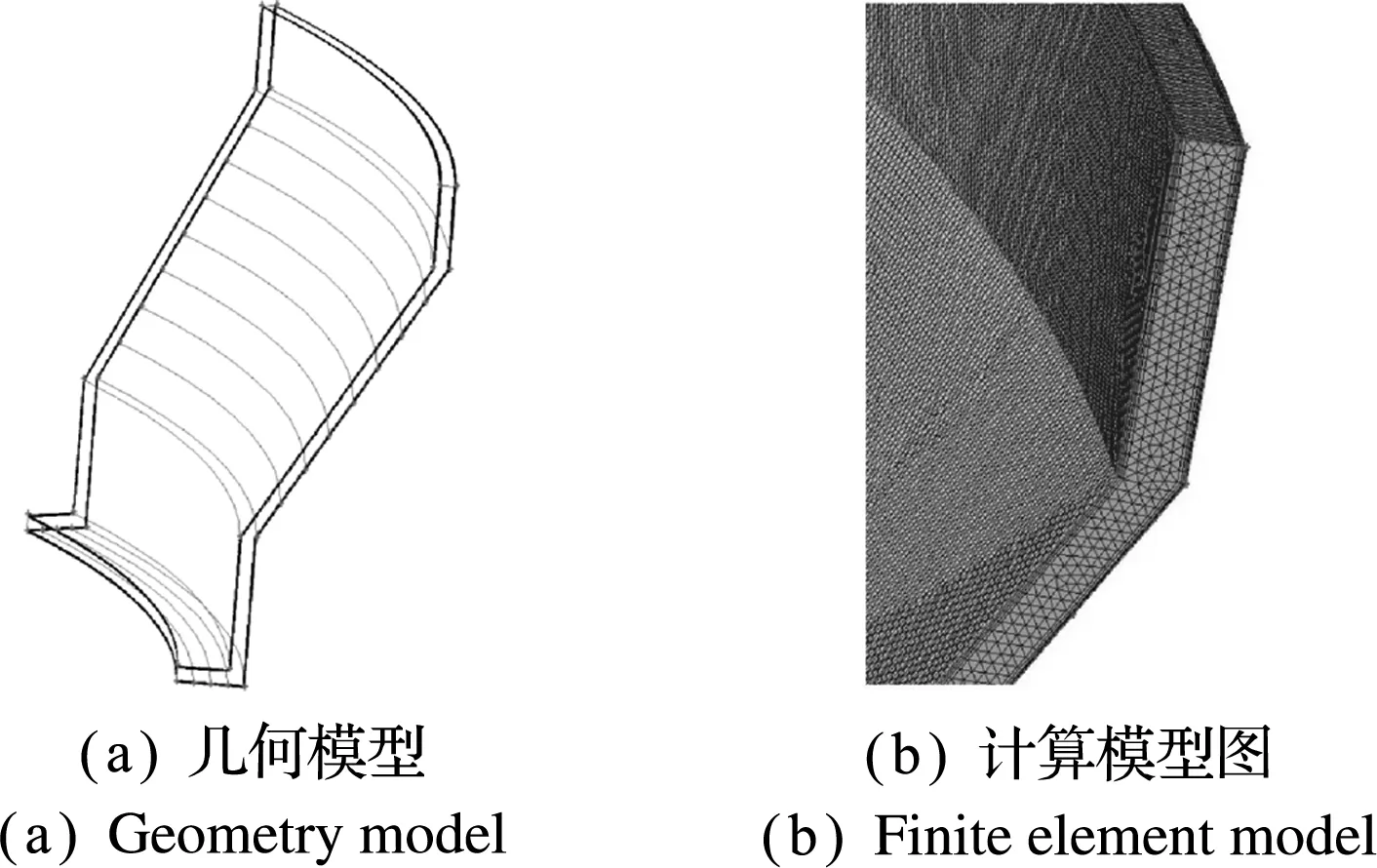
图11 修改模型

Fig.11 Modified models

因此，在核主泵运行条件下，轴向振动幅值将对结构稳定性产生重要影响，轴向负阻尼的出现导致振动发散，加剧了系统的不稳定。另外，通过改变叶轮间隙流道，缩小叶轮间隙流道导致轴向负刚度增大，而阻尼得到提高，起到稳定系统的作用。

5 结 论

本文对具有径向间隙流的理论模型及核主泵间隙模型进行理论分析和数值计算，发现具有径向流的间隙会对结构轴向振动产生不利影响。

通过建立理论间隙流模型,并与已有文献结果比较，确定了间隙流计算中湍流计算模型的合理性,验证了具有复杂边界的间隙结构的数值模拟及计算方法的正确性。

在实际核泵工况下，理论模型振动特性有以下两个特征，(1) 流体介质为水时,间隙产生等效的轴向负刚度因子。(2) 不同的流道形状(平行、收缩和扩张流道)表现出不同的轴向振动特性，多数工况下平行流道和扩张流道均会产生轴向负刚度和负阻尼，造成系统不稳定。收缩流道的轴向刚度和阻尼始终为正，收缩流道相对平行流道和扩张流道更安全。

使用已验证的计算方法，对AP1000核主泵原型叶轮间隙模型的轴向动力特性分析可得到以下结论，(1) 叶轮间隙在核泵运行工况下，具有负轴向刚度；(2) 不同轴向振动幅值对间隙结构轴向动力特性产生较大的影响，在某些振动幅值下，间隙具有负阻尼特性，引起结构不稳定； (3) 流道宽度影响间隙动力特性，叶轮间隙减小后，轴向负刚度增大，增加间隙对系统稳定性具有不利影响，但同时轴向阻尼也增大，对提高系统的稳定性起到积极作用。