设计好“大任务”，让学生看见“知识就是力量”

◇严育洪

2017年国务院印发的《国家教育事业发展“十三五”规划》第三部分“改革创新驱动教育发展”之中明确指出：“推动合作探究式学习，倡导任务驱动学习，提高学生分析、解决问题的能力。”这是“倡导任务驱动学习”首次出现在国务院文件中。

其实，“任务”在教学中并非一个新名词。我们来重温建构主义教学设计原理所强调的一段话：“学生的学习活动必须与大的任务或问题相结合，让学生在真实的教学情境中带着任务学习，以探索问题的解决方法来驱动和维持学习者学习的兴趣和动机，在完成实际任务的过程中完成知识的学习，并从中发展认知能力和处理问题能力。”许多教师阅读这段话时，只看见“问题”“情境”“完成知识的学习”这些现在流行的“教育热词”。如果我们能够关注到“大的任务”“带着任务学习”“在完成实际任务的过程中完成知识的学习”等表述，或许能够打开我们的教学视野，找到教学的新思路，实现“任务驱动学习”。

建构主义教学设计原理提到“让学生在真实的教学情境中带着任务学习”，这里 “真实的教学情境”，应该是那些能让学生“看得见、摸得着、用得到”的情境，在这样的教学情境中，最好能让学生既有“真情”又有“实感”，还能让学生有更真实的“获得感”。

例如，“长方体和正方体”单元包括长方体和正方体的认识、长方体和正方体的表面积计算、长方体和正方体的体积（容积）计算等众多知识点虽然这些知识点同属一个单元，但不同的地位让它们彼此“自立门户”，反映在教学上就是一节节课的接二连三。这样的“接二连三”更多的是不同知识内容的连续，能否是同一情境内容的连续呢？

美国国家神经疾病和中风研究所研究员乔丹·格拉夫曼认为：“你处理的事情越多，专注的时间就越少，你思考推理的能力就越差。”教学中，同一情境内容的连续可以让学生感觉始终在做一件事情，其间所有知识的学习都是为了做好这一件事情。这样的事情，可以是一个“大任务”

我们可以把“长方体和正方体”单元知识教学导演成一部“做一个鱼缸”的“生活情景连续剧”。学会做一个鱼缸，是学生感兴趣的、有实用价值的“大任务”。

第一节课，任务情境是：“明明准备做一个鱼缸，想用金属条做鱼缸框架（如图1）。现在知道金属条每米12元，接头每个4元。明明想知道购买这些材料需要多少钱。”其中涉及长方体的特征等知识点。

一 让学生看见知识的应用，增强任务完成的吸引力

图1

第二节课，任务情境是：“接着，明明要给鱼缸配玻璃，玻璃大约每平方米80元，要配齐所需玻璃，他还要花费多少钱？”其中涉及长方体的表面积计算等知识点。

第三节课，任务情境是：“鱼缸做好了，明明很得意：‘爸爸，快点放满水，把金鱼放进去，明天我要搬到班级生物角让同学们羡慕一下！’‘别高兴得太早。’爸爸说，‘你能轻松抱动这个放满水的鱼缸吗？再说水也不能放满，最多放八成。1升水大约重1千克，不算玻璃，你先算下水有多重吧！’”其中涉及长方体的体积计算等知识点。

至此，基本完成了“长方体和正方体”单元知识的教学任务。我们还可以让这一“生活情景剧”连续下去，拓展和深化知识。

第四节课，任务情境是：“爸爸买来几条小金鱼，问明明：‘你知道这些小金鱼会占用鱼缸多大空间吗？’明明把小金鱼放入鱼缸的水中，测出水面上升了0.4分米，明明兴奋地告诉爸爸：‘我可以算出小金鱼的体积啦！’爸爸点点头，又拿来一个小玩意儿（如图2，单位：厘米），问明明：‘它的体积有多大？如果把它放进鱼缸作为装饰物陪伴小金鱼，水会不会溢出鱼缸？’”其中涉及组合物体的体积计算和不规则物体的体积计算等知识点。

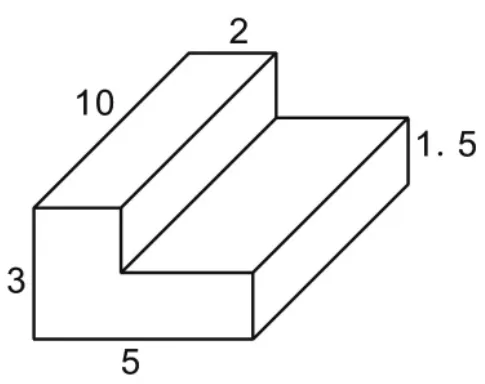
图2

第五节课，任务情境是：“明明把鱼缸拿到学校后，老师和同学们赞不绝口。同学佳佳想请明明帮她家也做两个这样的鱼缸，明明愉快地答应了。两个新鱼缸做好了，为了方便运输，要包装在一起，明明想：‘怎样包装最节省包装纸呢？’”其中涉及长方体拼合后表面积的计算等知识点。

如果我们想让这一“生活情景剧”更有料，不妨链接“世界上最小的鱼缸”这一富有趣味的资料：“俄罗斯著名微观艺术家Anatoly Konenko创作的一个鱼缸大小只有30mm×24mm×14mm，虽然它容积很小，但是里面格外丰富，微型植物、石头样样不少，甚至还放置有真正的小鱼，人们需要用放大镜才能看清楚里面的景观。另外，为了尽量不打扰到生活在这小小世界里的鱼儿们，Konenko每次需要用注射器给鱼缸换水，而且他专门制作了一个小巧的渔网，来与迷你鱼缸配套。”我们可以设计这样一些问题：“这个最小的鱼缸可以装多少水？”“如果使用2毫升容量的注射器给鱼缸换水，一共需要注射几次？”

如果看得更远，我们还可以和后继教材“圆柱和圆锥”单元的知识联系起来：“明明后来看到圆柱形鱼缸，他开始盘算：‘圆柱形鱼缸又该怎样设计和制作呢？要装得下原来长方体鱼缸中的水、金鱼和装饰物，这个圆柱形鱼缸又该做多大呢？’”

二 让学生看见知识的灵活，增强任务完成的战斗力

在任务驱动式教学中，“大任务”的呈现方式应灵活多样，甚至可以离“题”万里，从表面上看，有别于例题或习题的常规表达，甚至有别于数学的通常问法。很多时候，正是这样的不拘一格，可以避免学生滋生“又是做题”的厌倦感。

例如，在教学“圆的认识”一课时，我们设计了“圆规为什么能够画出圆”的探究性任务。貌似这个任务设计得很“离谱”——不探究圆的知识，却去探究圆规的设计原理，但实际上，这是一种迂回策略，因为要探究 “圆规为什么能够画出圆”，首先要探究圆的特征，然后才能解释圆规的设计原理。在这个过程中，学生多了这样一种认识：圆规的发明是圆的知识的活用。由此可见，学生完成了圆规设计原理的探究任务，也就完成了圆的认识的学习任务。此时，圆规身兼两职：一是画圆的工具，二是学圆的学具。

研究表明，能力就是基础知识的灵活运用，内化为能力的知识是最难忘掉的。画圆是一种能力，随着画圆能力的不断提高，学生对圆的认识也会不断提高。所以，我们可以在课后设计“你想挑战吗”这样的画圆任务：让学生从会画一个圆到会画几个圆组成的漂亮图案；当学生感觉任务已经没有挑战性时，布置徒手画圆的表现性任务，此时学生会根据圆规的设计原理想到多种方法，这也是知识的活用，在这个过程中，学生会有“有知识就有办法”的切身体会；当学生都熟练之后，教师可以再次提高任务的难度“你能用右手画圆的同时用左手画方吗”，再次激起学生不服输的激情；当学生都练得差不多时，教师可以再抛出一个更难的任务“你会用直尺画出圆吗”，这一任务虽然已经超出小学生的知识范围，一时难以完成，却可以让学生感到好奇的同时再次领略知识和方法的灵活，并且可以让学生一直牵挂着，直至中学阶段的学习。

教师设计的这些难度不断增加的挑战性任务大都属于“课外”活动：一是因为它们已属于“课本之外”，超出了教材的画圆要求和知识范围，二是因为它们已属于“课堂之外”。然而，我们应该看到，正是课外活动的投入，让学生能够带着好心情走入课内学习，所以教师应该重视课外任务的设计。

三 让学生看见知识的严谨，增强任务完成的洞察力

在实际生活中，知识误用的地方很多，我们可以针对性地设计一些让学生运用所学知识寻找并判断“这科学吗”“这靠谱吗”的“大任务”。可以说，让学生去发现生活现象中“有问题（知识错误）”，要比去发现课堂学习中有“问题（知识学问）”更有劲头，当学生知道其“有问题”时，求真的心理就会驱动他们主动去求证，用所学知识寻找问题所在。

例如，设计这样的思辨性任务：“在电视中经常看到这样的镜头，有人扔出一个手提保险箱，然后打开说‘一千万，点点吧’。你觉得这样的剧情科学吗？”平日，看影视剧是学生喜欢的娱乐方式，当他们知道影视剧拍摄竟然存在“这可能吗”的知识错误时，做这样隐含数学的练习学生会感到很“娱乐”，也就很乐意完成从测量、计算到判断等一系列数学活动的找碴儿任务：一是从体积上判断，如果都是百元纸钞，每张百元人民币长约15.5厘米、宽约7.7厘米，100张百元钞票（一万元）厚约1厘米，而一般手提保险箱长约50厘米、宽约30厘米、高约15厘米，由此算出一个手提保险箱只能放190万元左右的百元人民币；二是从质量上判断，总金额为一千万的百元人民币的体积约为0.12立方米，1立方米纸重约1000千克，所以总金额为一千万的百元人民币重约120千克，普通人是绝对无法提着在路上走的。

又如，设计这样的思辨性任务：“一个人腰缠万贯，这靠谱吗？”对于成语“腰缠万贯”，因为是“成”语，学生都没深究过，所以对这个任务会很感兴趣，喜欢去探究，最终形成两种观点：一是认为“古代人不可能”，因为贯是指旧时用绳索穿钱，每1000文为1贯，万贯也就是10000×1000=10000000（文），即10000000个铜钱，通过天平称和计算，发现万贯重40吨左右；二是认为“现代人可能”，因为查资料知道1贯（1000文）相当于200元人民币，10000贯=10000000文=2000000元，10000元 （100张百元人民币）重约120克，2000000元重约24千克。可以说，学生完成这个任务所进行的演算和验算，不仅是一次数学知识的演练，而且有助于理解“腰缠万贯”所表达的喻义，一举两得。

四 让学生看见知识的融合，增强任务完成的联通力

美国阿波罗登月计划总指挥韦伯曾说：“阿波罗计划中没有一项新发明的技术，关键在于综合。”这就是知识综合的力量，它有时能产生强大的穿透力和衍生力。有时，这样的知识综合还表现为不同学科之间的“跨界”。对能够“跨界”的综合性任务，学生会产生“任我行”的好奇感和满足感。

例如，当学生学习了“圆柱的体积”之后，教师布置“测算出一棵大树的体积”的实践任务。学生会先用软尺测量出树干的周长，然后计算出树干横截面的半径，得到横截面的面积，接着测量出树干的高度，最后计算出树干的体积。至此，学生还不能顺利完成任务，因为还有那么多粗细不等的树枝体积的测算很麻烦。此时，在学生的叫苦和求援声中，教师可以趁机把实践任务链接到以下的阅读任务——

一棵树长到一定高度就开始分叉，长出几根枝丫来，每根枝丫又继续分成几根小枝丫，小枝丫上又长出小树枝，最后直到每根小树枝上都挂满了一片片叶子……树木的这种倒锥形生长方式对于我们每个人来说都不陌生，但恐怕很少有人注意到其中的 “数学”：一棵树在任何一个高度，其所有树枝的截面积之和是不变的。这一现象是15世纪意大利画家达·芬奇首先观察到的。

学生唯有掌握了上述生物学知识，才能更好地解决该问题：当测算一棵树的体积时，我们只要算出树的底部的截面积，再乘以它的高度就可以了。当学生最终完成任务时，或许会有这样的感叹：大自然真奇妙，植物竟然也懂数学！或许还会有这样的感叹：这一现象竟然不是数学家发现的，而是画家发现的！由此可见，这里的任务链接功能让练习有了更多的情感色彩，让学生有了更多的情感反应。

五 让学生看见知识的温暖，增强任务完成的亲和力

有人认为，数学知识有的只是理性，其实数学知识也充满着感情。因为知识是一种认识，而认识无非是主观对客观、心灵对物质的一种反映。何况知识一旦走进教学，就有了感情，因为教学是教师和学生、学生和学生、学生与知识之间的交流过程，有了人，知识就有了感情。

我们设计的任务能否被学生接受，不仅取决于学生对任务的客观认识，更取决于学生对任务的主观态度，也就是说，我们设计的任务除了能够促进人的知识交流，还应该能够促进人的思想交流和情感交流。这样有“温度”的任务，更能够让学生心情舒畅。这，就是知识的情感力量。

例如，杭州师范大学东城第二小学布置了一个探究性的 “大任务”：“你知道妈妈的头发有多少根吗？”许多学生全家总动员。若妈妈的头发是长发，采用化整为零法。把妈妈的头发平分，扎满可爱的小辫子。先把妈妈的头发平均分为2份，其中的1份用牛皮筋扎起来。再把剩下的头发平均分成2份，以此类推，直到可以数清楚1份头发的根数为止。一共分了13次。最后一次数的头发根数为23，用23连续乘13次2，结果是188416根头发。当然头发的分法有很多，也有学生借用梳子进行估测，先把妈妈的头发均匀地用梳子分成28份，取出其中1份，再把那1份平均分成6份，数出其中1份是700根。列式计算：700×6=4200（根），4200×28=117600（根）。若妈妈的头发是短发，就采用皮克定理法。用剪刀把布剪成妈妈的头型，在40cm×40cm的纸上画好每格为1平方厘米的小方格。把布盖在方格纸上，描绘布的外形，把边界上的格点用黑笔描出，把内部的格点用红笔描出（如图3）。用皮克定理求布的面积：（20÷2+703-1）×1=712（平方厘米）。数出 1平方厘米上妈妈的头发有140根，则712×140=99680（根）。

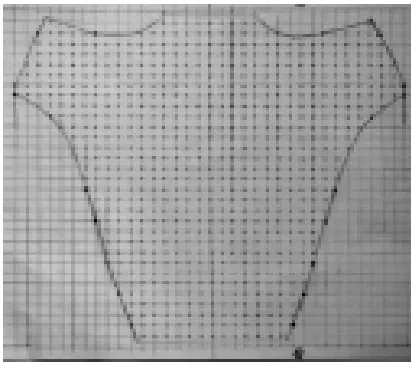
图3

这一实验任务带给学生的远不止数学综合素养的提升，还增进了家庭成员之间的感情。有家长这样描述：“从来没有看到过孩子如此认真的一面，像个科学家一样查阅资料，设计研究方案，还一次次和我们讨论，在平均分头发扎辫子时，生怕弄疼了我，作为家长我很感动。”还有家长这样感怀：“数头发时孩子在头顶摸来摸去，感觉特别温暖。”有学生这样抒情：“发现了妈妈有不少白头发，她太辛苦了。”还有学生这样行动：数完后帮妈妈洗头。

又如，我们还可以设计如此充满爱的任务：“母爱有多重？”山东日照市新营小学学生的答案是：在婴儿1岁多时，宝宝平均体重为7.5千克，母亲每天大概抱20次，也就是150千克；2到3岁时孩子平均体重为12.5千克，母亲每天大概抱10次，也就是125千克；4到10岁时孩子平均体重为25千克，母亲每天大概抱6次，也就是150千克……假设孩子10岁前还常常被母亲抱在怀里，那么母亲养育一个孩子总共抱起的总重竟然约474500千克，即474.5吨。也就是说，每位母亲相当于抱起了95头5吨重的亚洲大象。

总之，在教学中，要让学生感受到“知识就是力量”，有一种做法就是教师设计好“大任务”，用富含知识的“大任务”去吸引、去挑战、去成就学生，从而驱动学生主动学习。