在真实可感的学习体验中发展学生的应用意识——以“百分数的应用（一）”一课的教学为例

◇边 靖

在我的理解中，应用意识是一种主动建立数学与生活的联系的意识，是一种数学的思维习惯。在学生的学习过程中，应用意识主要体现为：面对现实，有从数学的视角提出数学问题的意识；面对问题，有用数学的方式思考和表达的意识，有用数学的知识和经验解决问题的能力；面对数学，有主动应用于生活的意识。

为体现这样的理解，我以北师大版教材六年级上册“百分数的应用（一）”为载体，尝试引导学生在真实可感的学习体验中发展应用意识。从教材的内容呈现看：“百分数的应用（一）”的数量关系是“求一个数比另一个数增加百分之几”。这样的关系在生活中可以刻画很多现象或事实，只是存在的形式不太一样。这样的内容如果只是当作数量关系来学习，而学生不知道知识的来龙去脉，则学生很难感受数学的价值，更不能发展应用意识。北师大版教材在情境创设上，提供了一个很好的素材，即“水结成冰，体积增加百分之几”的实际情境。我想“增加百分之几”的数量关系恰好可以很好地刻画水结成冰体积的变化，让学生感受百分数在刻画生活现象或作出某种判断的过程中发挥的作用，进而体会数学的应用价值。

怎样从数学的视角引导学生关注“水结成冰，体积增加”这样一个习以为常的生活现象，进而用数学的方式刻画这一变化呢？为此，我选择了让学生亲历水结成冰的情境。让学生在课前亲自将水结成冰，并记录水和冰的体积数据，引导学生带着自己的真情实感，关注水结成冰后体积的变化和解决水结成冰现象中的数学问题。

一、结合操作实际，聚焦数学问题

1.关注生活实验，收集数学信息。

学生兴致勃勃地带着自己课前结成的冰和记录单走进课堂，但冰有点儿化了，学生有点儿失望，我顺势鼓励他们：“冰虽然有点儿化了，但不要紧，因为你们都是有心人，关注到了水结成冰过程中的变化，也记录了数据。”

之后组织学生反馈他们记录的数据。板书：

2.分析生活现象，聚焦数学问题。

这些数据来自学生真实的实验，他们很愿意反馈自己的信息。通过反馈，学生很容易关注到“水结成冰，体积增加了”这一生活现象，此时，引导学生从数学的视角观察这个现象。

师：原来水的体积是这么多，结成冰之后，体积变成了这么多，我们从数学的视角来看看，你想研究什么？

学生的关注点从对直观、表面的现象的感性关注，转变为开始将零散的信息进行整合，进行理性思考。学生能够提出可研究的数学问题，应用意识在悄然发展。

生1：水结成冰，体积能增加多少？

生2：体积增加了几分之几？

生3：体积增加了百分之几？

学生的思考已经从两个单独的量，进入了量与量之间的关系，在他们关注的关系中，有“多少”这样的具体数量关系，也有“分率”这样的倍比关系。具体数量关系可以直接刻画多少，而倍比关系则刻画两个量之间的相对关系。在刻画“水结成冰，体积增加”这一变化时，显然倍比关系更合适，通过对比判断可以让学生体会“倍比”关系的应用价值。

师：你们想研究的关系中，有数量关系，还有百分率关系，哪个用来描述水结成冰后体积的变化比较合适呢？发表一下你们的看法。

生1：用增加百分之几合适。“增加了多少”针对的是个体，“增加了百分之几”则表示可以进行比较，得到一个大概的数。因为水的体积是不一样的，所以研究增加百分之几好。

生2：“增加了多少”，有可能仅仅是针对100立方厘米的水测量的，但对于200立方厘米的水就不一定是了，不如研究增加百分之几实用。

生3：水的量不是都一样，所以数量差也不一样，但百分比可能一样。

学生能从变中寻找不变，这是数学研究中一个很重要的角度。抓住变中的不变恰好可以体现学生在从聚焦关系到辨析关系的过程中，对倍比关系的直觉及理性理解。

二、分析、解决数学问题，体会现实应用

如何利用学生收集到的如此多水和冰体积的数据，来得到“水结成冰，体积增加百分之几”这一学生已经感觉到可能不变的关系呢？我想还是先选择一组数据，解决如何列式这个方法性的问题。在学生解决问题的过程中，我设计了让学生用数学的方式进行思考和表达的活动。让学生利用图直观表征水和冰的关系、分析数量关系，再利用图理解不同解题方法的含义、建立不同算式间的联系，力图让直观图在分析、理解中发挥支撑作用。

1.单一数据计算，形成解决方法。

师：我们采用这位同学的数据（水：110立方厘米，冰：120立方厘米），想办法算一算，水结成冰的过程中，它们的体积会存在怎样的百分率关系？

学生经过独立思考之后，呈现了不一样的方法（如图1和图2）。

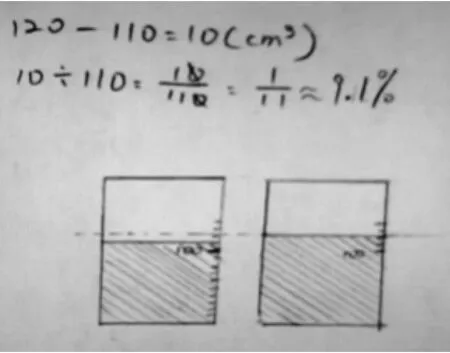
图1

图2

从学生画的图中，我们可以看到，水结成冰的过程在学生分析数量关系的过程中起到了很好的支撑作用。因为学生亲历了水结成冰的实验，所以水结成冰的过程变得可视、可感。这样有利于学生体会计算“增加百分之几”的标准应该是“水的体积”。在这个过程中，学生能将生活经验转化为数学的直观表征，进而应用于数学的学习过程中，这恰好是应用意识的一个表现。

2.不同数据计算，关注现实问题。

结合一组数据，学生有了解决“增加百分之几”的本领，但实际问题是，他们收集的数据不尽相同，只用一组数据得到的结果，就是生活中水结成冰后体积增加的百分比吗？如果不是，又该怎样利用手中的数据呢？这些问题值得学生关注，也值得学生深入思考。

师：我们是不是可以得出结论，水结成冰，体积一定增加9.1%？

生1：这也许是一组特殊的数据，需要多试几组，如果9.1%多的话，就可以把其他的视为不正常的数据。

生2：只算出这一个不太精准，需要多算几个，再算平均数。否则不太严谨。

生3：只要不是科学数据，怎么都会有些误差，所以需要多算算，比如，170和185这组，也得算，然后取平均值。

从学生的发言中，可以清晰地看到数据分析观念在学生分析、解决问题的过程中，不断得到应用。学生真的很棒，他们面对数据，主动想办法分析和处理数据。众数、平均数这些散落在他们学习历程中的知识，此时不断被提及、被利用。随后，学生分小组计算数据，输入电脑中的Excel软件之后，我没有按学生的办法马上算平均数。

师：我们先别急着算平均数，先看看这些数据，你有什么想说的吗？

生1：总觉得5%有点儿不正常，差得太多了。

师：你们觉得呢？这个数据是谁的？能和大家分享一下你的原始数据吗？

生2：我用的水的体积是100立方厘米，冰的体积是105立方厘米，现在想想，我开始倒的水的体积可能比100立方厘米少，我没平着看，可能不准。

……

学生从对一些“特殊数据”的质疑开始，诚实地反思自己收集数据的过程。在这个过程中，学生不仅主动将数学应用于生活，更养成了良好的数学学习习惯。

3.呈现科学数据，反思解决过程。

课件呈现：在常压环境下，0℃的水结成冰后，体积大约会增加11.1%。

当孩子正兴奋于自己的研究成果时，我出示了科学结果。学生顿时有点儿失落。这时的反思是十分必要的。一方面，可以分析与科学数据产生差距的原因；另一方面，可以分析经历得到结果的过程中所收获的经验、所增长的本领。

师：和咱们的研究成果相比较，你有什么想说的？

生1：我觉得我们错了，我们在观察数据时一定有误差，不够准确，使得我们的结果和科学数据有差距。

生2：我觉得我们做得够不错的了，我们是用肉眼观察的，我们得到的结果和科学数据差得并不多。

师：我也觉得你们做得很不错，知道你们了不起在哪儿吗？

生1：我们收集了很多数据，然后用平均数找到了一个大致的结果，虽然不准确，但知道了大概。

生2：我们用增加百分之几描述水结成冰后体积的变化是成功的。

师：其实，百分数能帮我们刻画很多现象，或帮我们作很多判断。

三、拓展数学应用，发展应用意识

出示图3和图4：

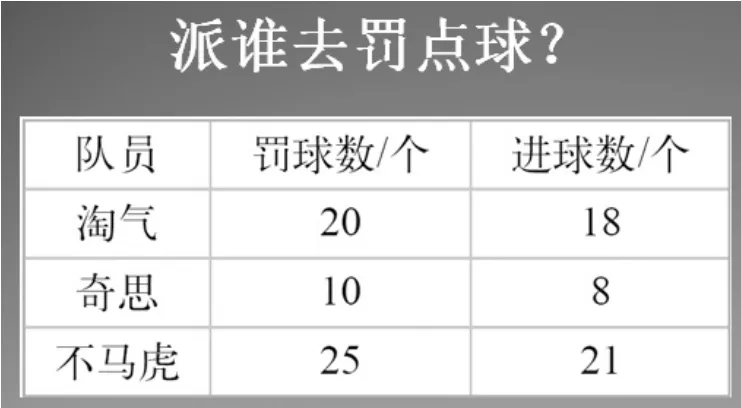
图3

图4

带领学生跳出水结冰的生活情境，使他们体会百分数在生活中更广泛的应用，树立大的应用观。

整节课，学生从真实的生活体验出发，收集真实的数据，在对“真实”的研究中遇到真困难，就试着画直观图来分析、理解数量关系，用数学中的数据处理方式解决数据问题，学生经历了一个真正的问题解决过程。在这个过程中，他们感受到了数学中“增加百分之几”这样一个关系不仅可以刻画水结成冰后体积的变化，还可以解释或刻画生活中的很多事实。他们尝试从数学的视角出发，在遇到问题时，用数学表达，用数学分析，用数学作判断。