让儿童的运算能力在问题情境中形成——以“有余数的除法”为例

◇马 宇

2017年的10月至11月，我作为教育部“一师一优课、一课一名师”的评委，共参与评价了49节课，其中有来自全国23个省、市、自治区的23位老师选上的“有余数的除法”一课，该课执教的大致情况如表1：

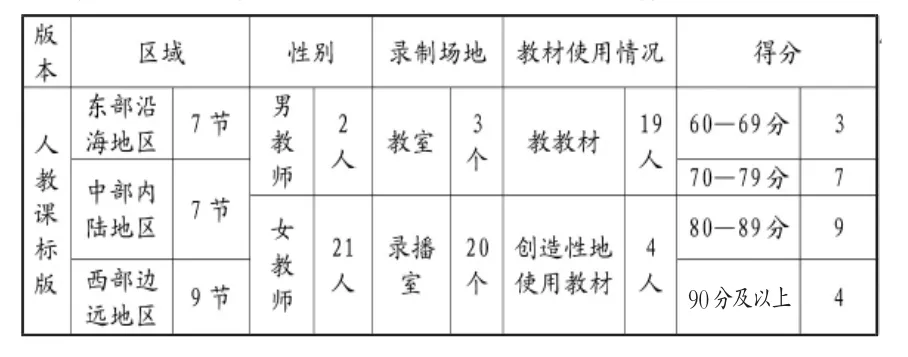
表1 “有余数的除法”部分执教情况统计表

经过多个评委的综合评价，有两节“有余数的除法”课脱颖而出，获部级优课。本文仅以其中一节为例谈谈“如何让儿童的运算能力在问题情境中形成”。

一、为什么获奖——关注儿童运算能力的培养

在我国近百年来的小学数学教学中，计算一直是重要的学习内容。也因为其重要性，计算教学内容的增减、熟练程度总是每轮课改的重头戏。比如从1978年提出删减“过繁计算”；再如2001年的《全日制义务教育数学课程标准（实验稿）》提出“应重视口算，加强估算，提倡（鼓励）算法多样化”。当然，随着新一轮课改进入深水区，诸多教师关于计算教学也有了新认识。《义务教育数学课程标准（2011年版）》增加了核心概念“运算能力”，主要是指能够根据法则和运算律正确地进行运算的能力，培养运算能力有助于学生理解运算的算理，寻求合理简洁的运算途径解决问题。于是从“计算技能”的教学到“运算能力”的培养也成为广大小学数学教师的自觉诉求。儿童运算能力的形成主要表现在哪些方面呢？具体来说主要有三：

一是儿童能正确地算。比如在本节“有余数的除法”教学中，儿童基于原有经验，能在操作、观察、对比等活动中深入思考、大胆质疑、主动建构，对“余数”及“有余数除法”的含义理解深刻，解答“有余数的除法”的水平比较高。

二是儿童能明白地算。比如在本课中，儿童对算理的理解（认识余数的真实存在、明白“余数要比除数小”的道理）、对算法的掌握（会列有余数除法的横式）交错进行、相互促进，对运算形成了贯通式的理解。

三是儿童能合理地算。比如本课在巩固阶段设计了“创编绘本故事”的练习，由于情境新颖、问题开放，所以儿童能通过多样化的表征去理解和思考问题，能够“寻求合理简洁的运算途径解决问题”。

二、怎样培养儿童的运算能力——在问题情境创设上的着力点

1．引入新知时，问题情境设计以激发计算的兴趣为目的。

为了调动学生的学习兴趣，教师选择了儿童喜闻乐见的绘本素材去设计情境。该情境在快速链接学习和生活的同时，也凸显了数学学习中的问题，成为平均分物时“正好分完”和“分后有余”这一对知识点间的纽带。

片段一：创设情境，为新知探究埋下伏笔

师：前两天老师读了一本绘本，它的名字叫作《百足虫的100只鞋》。到底讲了什么故事呢？我们一起去看看吧。

（教师读学生听）

师：它打算先把20只鞋送给只有4只脚的鼠小弟，能分给几只鼠小弟？

（课件演示分的过程）

师：我们可以列式表示刚才分的过程和结果吗？

生：20÷4=5（只）。

师：为什么用除法来计算？

评析：国际公认“绘本是最适合幼儿阅读的图书”，为了激发儿童的计算欲望，教师特意将陪伴他们多年的“精神食粮”放到数学课上。通过“把20只鞋分给鼠小弟”这一问题情境，既让儿童在美美的图画中、在暖暖的情感里复习了“表内除法”，又为新知探究埋下伏笔。

2．建构新知时，问题情境设计以贯通算理和算法为目的。

“有余数的除法”是在学生学习过 “表内除法”的基础上进行的。“表内除法”是二年级下册的重点内容，学生经过概念理解、巩固深化等过程，已经牢固树立了一个观念：凡是能用除法表示的都是平均分的并且能够刚好分完。所以，如何把儿童生活中积累的“按组平均分成几份之后还有剩余”的经验激活，如何让他们更好地理解余数及有余数除法的含义，成为本课问题情境设计中需要考虑的核心问题。

皮亚杰认为，小学生的思维发展处在具体运算阶段（7～11岁）。进入具体运算阶段的儿童能够借助直观、借助现实情境，通过具体的实例来理解抽象的算法。据此教师设计了活动情境，让儿童在实践中关联“表内除法”和“有余数的除法”，认识到余数的真实存在，从而初步理解“余数要比除数小”的道理，并会用除法算式表示出来。

片段二：在操作中感受“平均分后有剩余”的情况

绘本阅读：百足虫送完20只鞋之后开开心心地回家了。“可是还剩下这么多鞋怎么办？”小百足虫回到家问妈妈。“你不是还有其他朋友吗？”妈妈说。

师：小百足虫想到了蚱蜢，蚱蜢有6只脚，穿起鞋来也比较方便。想一想，20只鞋能分给几只蚱蜢？

课件出示活动要求：用圆片代替20只鞋。

（1）边分边想：你是怎么分的，分的结果是什么？

（2）分完后，和同桌说一说分的过程。

生：我用圆片代表20只鞋，先拿6只鞋分给一只蚱蜢，再拿6只鞋分给一只蚱蜢，剩的还很多，就再拿出6只鞋分给一只蚱蜢，最后剩下2只鞋。

师：还能再分吗？为什么？

生：剩下的2比6少，不能再分了。

生：因为每只蚱蜢都需要6只鞋，所以剩下的2只鞋就不用分了，因为不够一只蚱蜢穿了。

生：剩下的鞋的只数比一只蚱蜢脚的只数少，就不能再分了。

评析：《百足虫的100只鞋》的情境在新知学习中得以继续生长。同样都是20只鞋，但因为这次是分给小蚱蜢，所以每次都要拿出6只，这样拿出3个6只后还剩下2只，怎么办？充满爱心和公平心的儿童明确提出——剩下的2只鞋不够一只蚱蜢穿了，就不用再分了。情境中“不够分的2只鞋”就和数学中“分到不能再分出一份所剩下的数”紧密相联系，于是“事理”有效地支撑了“算理”的形成，“余数”的含义呼之欲出。

片段三：在交流中确定“平均分后有剩余”的表示方法

师：回忆刚才分的过程，谁能完整地说一说？

生：我们是把20只鞋，每6只分一份，可以分给3只蚱蜢，还剩下2只鞋。

师：请你们把刚才分的过程用一个算式表示出来。

（学生尝试列式）

师：谁来说一说你的算式是怎么列的？算式中的每一个数表示什么？

生：20÷6=3 剩 2。20 表示一共有 20 只鞋，6表示一只蚱蜢需要6只鞋，3表示可以分给3只蚱蜢，最后还剩下2只鞋子。

生：20÷6=3 余下 2。

生：20÷6=3……2。

师：这三个算式，有的是用文字表示还剩下2只，有的是用省略号表示还剩下2只，你们比较喜欢哪一个？

生：用省略号的。

师：为什么？

生：比较简单，写起来不麻烦。

师：是的，在数学的世界里，人们更喜欢用符号来表示事物。现在请大家跟老师一起写写这个算式，并说说算式中每个数的含义。

（教师带领学生认识有余数除法算式各部分的名称，重点理解什么是“余数”）

师：刚才我们帮百足虫分了两次鞋，这两次分的过程有什么相同点？又有什么不同点？

（教师揭示课题：有余数的除法）

评析：“余数”如何在算式中表示出来？为了打破儿童原有的“认知平衡”，教师在他们充分操作的基础上，让其自主创造算式。这样在遵循儿童“直观动作思维—具体形象思维—抽象逻辑思维”的认知规律的基础上，他们初步理解“余数”和“有余数除法”的含义。

片段四：在探索中发现“余数和除数的关系”

（课件出示：21只鞋可以分给几只蚱蜢）

生：分21只鞋，每6只鞋为一份，可以分给3只蚱蜢，还剩余3只鞋。

师：怎么列式？

生：21÷6=3（只）……3（只）。

师：算式中有两个“3”，它们表示的意思一样吗？能结合图片解释一下吗？

生：“商3”表示可以分给3只蚱蜢，“余数3”表示剩下3只鞋。

师：像这样剩余的数比一只蚱蜢的脚的只数少，就不能再分了。

师：百足虫仍然不放弃，它想如果有22只、23只、24只……

生：好说。22比21多1，分21只鞋时余数是3，那么分22只时就可以列式为22÷6=3（只）……4（只）。

生：23÷6=3（只）……5（只）。

生：24÷6=4（只）。

师：之前分 20、21、22、23 时都产生了余数，为什么分24只鞋没有出现余数？

生：因为“四六二十四”，所以 24÷6=4。

生：分23只鞋余数是5，24只比23只增加1只鞋，余数就变成6，6只鞋可以再分给1只蚱蜢，所以 24÷6=4。

师：请大家认真观察这组算式，思考三个问题：（1）判断余数能不能继续分下去，该怎么想？（2）怎么确定有没有余数？余数有什么特点？（3）有没有余数？你能再举出几个这样的例子吗？

评析：为了让儿童深入理解“余数比除数小”的道理，教师继续变化“给小蚱蜢分鞋”的情境。被除数连续递增，让儿童感悟余数依次出现2、3、4、5和0的变化，启迪儿童从根本上理解“余数”——因为是给蚱蜢分鞋，所以余数始终在和除数6进行比较。只有余下的数比6小，才不用继续分了。这样儿童会根据余数的特点，生成判断余数的规则，“算理”和“算法”比翼齐飞。

3．应用新知时，问题情境设计以寻求合理简洁的运算途径解决问题为目的。

知识应用阶段应创设面向新知巩固的数学问题情境。为了让学生获得用数学可以解决现实问题的通透感和愉悦感，教师基于二年级学生的心理特点和学习规律设计了“编绘本故事”的开放性练习，帮助学生接轨经验、提高认知。

片段五：

师：接下来也请你当一次小作者，发挥你独特的想象，自己创作一个绘本故事吧。

（1）可以帮助百足虫继续送鞋。

（2）可以帮老师分奖品。

（3）可以帮妈妈分水果。

……

评析：创作“分物问题”的绘本故事，一方面能创设轻松的练习氛围，让儿童在涂涂画画中自由表达；另一方面也给不同思维水平的儿童提供了层次相异的思考空间，他们创作的绘本故事可复杂、可简单，但都聚焦于对“平均分物中的两种情况”以及对应的算式的理解。当然更重要的是，能让儿童灵活地将获得的“有余数除法”的含义和“余数要比除数小”的理性理解返回到实物，以培养儿童用数学的眼光观察世界、用合理简洁的方法和途径解决问题的能力。