关于干扰作用下航天器姿态饱和控制的结果*
胡锦昌,张洪华,王泽国,陈上上
0 引 言
航天器在实际运行过程中,一般要受到外界干扰作用和控制力矩饱和的限制.关于同时考虑输入饱和与外界干扰的姿态控制问题,已有诸多文献进行过研究.文献[1]设计了一种类滑模的连续控制律来抑制有界干扰的影响;文献[2]利用饱和函数和自适应控制律来解决有界输入下的抗干扰问题.文献[1-2]的共同问题是其中的自适应参数有可能趋于零,此时无法保证四元数矢量部分收敛到零.文献[3]则在输入饱和的约束下,进一步考虑了输入不确定性和速率受限的情形.文献[4]提出了一种饱和PD+干扰抑制项的饱和控制器,其中的干扰抑制项根据干扰类型的不同而具有不同的形式.
本文研究采用饱和PD控制律时,姿态系统受到不同干扰时的闭环稳定性问题.文献[5]已证明在PD控制律作用下,姿态系统的平衡点是近乎全局收敛的.事实上,如果速率反馈项具有饱和限制的话,那么姿态系统的平衡点仍然是收敛的.文献[6]指出,由于姿态空间SO(3)的特性,任何连续控制律都不可能使得任意平衡点获得全局稳定的结果.对于四元数表述的姿态系统,由于两个符号相反的四元数表示物理空间完全相同的方向,因此连续控制律将有可能产生“退绕”现象.为避免退绕问题,文献[7]设计了具有时滞的混杂型控制器,而文献[8]设计的混杂控制器则需要知道惯量阵信息.文献[7-8]的问题是没有对受到干扰时的情形进行分析.从目前的文献调研来看,目前很少有学者研究过姿态系统在饱和PD控制作用下,如果受到外界干扰时的闭环特性.本文将对此进行较为深入的研究:首先针对连续饱和PD控制律下闭环系统的行为特性进行研究,然后设计混杂型的控制律以进一步获得鲁棒控制的结果.
1 问题描述与定义
考虑四元数描述的刚体姿态方程
(1)
(2)

本文的控制目标为:在控制力矩u有界的情形下,设计控制律使得四元数矢量部分和角速度趋于零或者最终有界.
2 不同干扰下的闭环控制结果
2.1 干扰平方可积的情形
考虑采用如下形式的连续饱和控制律:
u=-kpqv-σM(kvω)
(3)
其中:σ(·):R3→R3为矢量形式的饱和函数,其定义为:∀s∈R3,(σM(s))i=sign(si)min{M,|si|},i=1,2,3;M为饱和幅值.
将式(3)代入式(2)可得姿态动力学闭环形式为:
(4)
假设干扰仅渐近收敛到零,即
d(t)→0,t→∞
由于在控制器式(3)的作用下,平衡点(q0,qv,ω)=(1,0,0)属于鞍点,因此将无法保证闭环系统平衡点(qv,ω)=0的收敛性.为避免此问题,需要干扰至少是二阶收敛的.其结果如定理1所示.
定理1. 考虑(1)~(2)所示的姿态系统.设计式(3)所示的控制器.假设干扰为二阶可积的,即有:
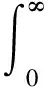
那么对任意初始状态,均有:
qv(t)→0,ω(t)→0,t→∞
证明.构造Lyapunov函数如下:
(5)
对V1沿闭环系统求导可得:
(6)
对式(6)应做两种情形下的分析:
1)对于i∈{1,2,3},若|kvωi|≤M,此时有:
ωi[-σM(kvωi)+di(t)]
(7)
其中0<χ 2)对于i∈{1,2,3},若|kvωi|>M 注意到di(t)→0,因此总能找到有限时间T0>0,使得 ∀t>T0 (8) 此时应有: ωi[-σM(kvωi)+di(t)] ≤-|ωi|[M-|di(t)|] (9) 由式(7)和(9)可见,两种情形下均有: i=1,2,3, ∀t>T0 (10) 于是由式(6)有: ∀t>T0 (11) 对式(11)两边同时积分,可得: ∀t>T0 (12) 易证姿态系统不存在有限逃逸时间,因此V1(t)在时间[0,T0)内是有界的.又由条件知d(t)是二阶可积的,因此由式(12)可知V1(t)在[0,∞)内是有界的.由式(5)可知ω是全局有界的,即ω∈L∞.设在时间区间[0,∞)内ω的最大值为Mω,则必能找到充分小的正数φ>0,使得 ∀t>T0 (13) 从而式(9)可以化简为 ωi[-σM(kvωi)+di(t)] (14) 利用(7)、(14)可进一步推得在1)、2)两种情形下有: ωi[-σM(kvωi)+di(t)] (15) 其中γ:=min{(kv-χ),φ} 将式(15)代入式(6),可得 ∀t>T0 (16) 又由 ∀t>T0 (17) 注1. 定理1只是证明了对于任意初始条件,四元数矢量部分均趋于零,即qv(t)→0,但是无法保证q0→1还是q0→-1.事实上,对于近乎所有工况,都有q0→1.这导致对q0(0)在-1附近的工况也收敛于q0→1,这就导致了退绕现象. 注2. 对于仅d(t)→0的情形,可能对于某些初始条件可以先保持在q0=-1附近,而后再转移到q0=1附近.在转移的过程中可能导致四元数和角速度变得很大.由于开始转移的时间可能是任意的,这就不满足收敛性的定义.因此此时无法得到qv(t)→0和ω(t)→0的结论. 注3. 定理1可以应用在具有干扰辨识的控制器设计当中.假设干扰为常值,设控制器为如下的饱和PD+前馈形式: (18) (19) (20) 由式(20)可得干扰辨识误差为: (21) (22) 利用定理1即可证明闭环系统平衡点的收敛性. 当干扰不属于二阶可积时,为保证闭环系统的稳定性或鲁棒性,可以设计具有时滞的混杂型控制器.设计控制器为如下形式[4]: u=-kphqv-σM(kvω) (23) 其中h为具有时滞的切换型变量,其变化律为 (24) 其中δ>0为选择的切换阈值,c>0应充分小. 将式(23)代入式(2)可得: (25) 可以证明当干扰d(t)→0时,平衡点(hq0,ω)=(1,0)是全局渐近稳定的.这放松了定理1干扰二阶可积的要求. 定理2. 设输入力矩采用式(23)、(24)所示的混杂型姿态控制律.则当干扰d(t)→0时平衡点(hq0,ω)=(1,0)是全局渐近稳定的. 证明.构造Lyapunov函数如下: (26) 对V2按时间进行求导可得: (27) 由于d(t)→0,因此对于任意小的ε>0,必能找到有限时间T1>0,使得: ‖d(t)‖1≤ε,t>T1 (28) 定义区域 (29) 假设ω∉Ω,则易知 ‖kvω‖∞>ε (30) 从而可得: (31) (32) 因此ω(t)必然在[T1,∞)内必然是有界的.而由于闭环系统在[0,T1)内没有有限逃逸时间,因此ω(t)必然在[0,∞)内是全局有界的. 构造Lyapunov函数 (33) 其中的c与式(24)中的c相同. 可以证明,当c充分小时有: (34) 其中P1,P2是适当的正定矩阵,由于篇幅所限,这里省略其具体形式.由式(34)可见V3是关于x的凸函数. 一方面,在离散控制域,由式(24)应有: ≤-4kpδ<0 (35) 另一方面,在连续控制域,对V3求导可得: ≤-ωTσM(kvω)-ckp‖qv‖2+ (chqv+ω)Td(t) (36) 由于角速度全局有界,因此必然可以找到充分小的数φ2,使得 -ωTσM(kvω)≤-φ2kvωTω (37) 将式(37)代入(36)可得: chkv‖qv‖‖ω‖+(chqv+ω)Td(t) (38) 其中 (39) 易证如果c充分小那么Q总能保持正定. 定义区域: (40) 由式(35)和(38)可知,对于∀x∉Θ,V3(t)对于连续和离散控制域都是递减的.因此必然有x(t)→Θ.由(28)可知,Θ的半径由干扰d(t)的大小决定,由d(t)→0,可知Θ→0,由此容易证明x(t)→0. 注4. 对于干扰d(t)任意小但不趋于零的情形,类似定理2可以证明四元数和角速度的最终界也将是任意小的.当注3中的干扰是时变但导数有界的情形即可属于该种情形.此时可以设计参数β使得干扰辨识误差任意小,从而可以证明四元数和角速度的最终误差可以任意小. 选取航天器的惯量为: 初始状态为: q0(0)=-0.899 5, qv(0)=[0.06 0.08 0.01]T, ω(0)=[0.343 8 0.458 4 0.057 3]T(°)/s 选取控制参数:kp=6,kv=80,c=0.01,δ=0.01,饱和限幅值M=0.5. 针对连续控制器的情形,设干扰为如下指数衰减形式: d(t)=(1,1,1)Te-0.1tN·m 易知干扰是平方可积的.图1与图2分别显示了四元数和角速度的控制结果.由图可见,四元数矢量部分和角速度最终收敛到零.虽然物理上姿态初值已经接近平衡点,但是图1四元数标量部分却从-1最终变化到1,表明发生了姿态的退绕现象.由图2可见,在退绕过程中,角速度产生了较大的峰值,这表明退绕不仅使得姿态运动更长的路径,对姿态稳定也产生了不利的结果. 针对混杂型控制器的情形,设干扰为如下形式: d(t)=(1,1,1)T/(1+10t)1/2N·m 易知干扰是不能二阶可积的,但是d(t)→0.图3与图4分别显示了四元数和角速度的控制结果.由图可见,由于采用了混杂型的控制器,本体姿态和角速度最终收敛到(q0,ω)=(-1,0)T,且并没有发生退绕现象.仿真结果表明了混杂型控制器设计的有效性. 本文针对饱和PD控制器作用下的刚体航天器姿态系统,研究了不同干扰作用下的闭环系统行为.由于姿态空间SO(3)的特殊性,采用连续控制器会产生退绕现象.但是对于外界干扰二阶可积的情形来说,采用连续型饱和PD控制器仍然可以获得四元数矢量部分和角速度收敛于零的结论;对于外界干扰不能二阶可积但收敛于零的情形,可以设计混杂型控制器避免退绕现象并保证物理平衡点是全局渐近稳定的.文章最后利用数值仿真验证了所设计控制器的有效性.本文结论对姿态系统的控制具有一定的指导意义.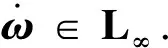
2.2 混杂型饱和控制律的收敛结果
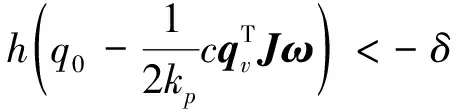

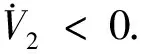
3 数值仿真
4 结 论

