基于快速响应的导航星座重构构型设计

赵 双 ，张雅声，戴桦宇

0 引 言

星座从初始构型变换到另一种构型，称之为星座构型重构[1].当星座中出现故障卫星或者星座任务发生变化时一般会通过在轨资产响应或地面资产响应的方式对星座构型进行调整来改善和恢复星座性能.

文献[2]针对连续多颗卫星失效的情况，以最大不可视时间为评价指标，提出了调整相邻卫星、均匀相位和均匀星座3种星座重构策略综合考虑燃料消耗和重构时间，提出了以总重构时间最小为优化目标的卫星星座快速重构构型优化设计方法.文献[3]针对全球卫星导航系统在部分卫星失效的情况下，通过调整剩余卫星的轨道进行星座重构，达到降低失效影响、优化地面导航性能的目的.文献[4]研究了将GPS从6轨道面变换到3轨道面时，对星座性能影响最小的构型变换重构控制策略.文献[5]研究了混合导航星座的中高轨道子星座重构策略和同轨道面内重构的方法，分析了重构优化目标与方法.

上述重构方法均属于在轨资产响应的范畴.通常认为在轨资产的响应速度要比地面资产的响应速度快，然而事实却正好相反.一方面，在轨运行的航天器其运行速度往往都很大，要改变其运行状态必然要付出很大的代价[6]；另一方面，地面快速响应可以相对自由地选择航天器的发射时间、发射地点和运行轨道，与空间快速响应相比完成相同任务所耗费的时间要更短，所以本文提出基于地面快速响应的导航星座构型重构方法，并针对快速响应任务中的相关特性进行分析.包括快速响应任务中的发射方式、入轨方式以及响应时间，建立了基于快速响应任务的导航星座重构构型设计，并利用NSGA-Ⅱ算法对重构模型进行求解.

1 快速响应任务中的轨道设计

1.1 发射方式

快速响应卫星的发射方式一般可分为：定点发射和机动发射[7].

(1)定点发射

定点发射是指在固定的发射场通过运载器将卫星送入预定轨道.定点发射的发射时间一般包括发射准备时间和发射等待时间.其中发射准备时间是指从任务下达开始到完成发射设备进场和调试所耗费的时间，发射等待时间则是完成发射准备后等待发射窗口所需要的时间，不考虑升轨发射和降轨发射的区别，发射等待时间可以定义为从发射准备完成开始到发射场依靠地球自转第一次穿越快速发射轨道平面所经历的时间.定点发射由于受限于发射场地理位置，只能被动的等待发射窗口来临.假设发射场E的地理经纬度为(λE,ψE)，当快速发射轨道的升交点赤经Ω∈[0°,180°]时，发射等待时间可由式(1)得到：

tw=

(1)

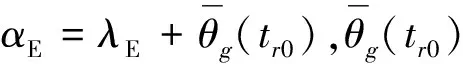
(2)机动发射

机动发射是指通过飞机、舰船、发射车等载体将运载器机动至某一指定位置，然后通过运载器将卫星送入预定轨道.与定点发射相比，机动发射的发射地点并不局限于某一固定位置，而且机动发射具备灵活、机动、反应速度快、主动性强的显著优势，在一些应急情况和对响应时间要求较高的空间任务中运用比较普遍.由于不受地理位置的限制，机动发射可以很大程度上缩减发射等待时间.如果发射区域无限制，可以认为：

tw=0

(2)

除此之外，机动发射同时也可以执行定点发射的任务.

1.2 入轨方式

卫星的入轨方式一般可以分为两类：直接入轨、间接入轨.

(1)直接入轨

直接入轨是指通过运载器的连续工作将卫星从发射点送入预定轨道.这种方式简单直接而且具备一定的应急响应能力，但由于运载器本身所携带的燃料有限，采用直接入轨的卫星其轨道高度一般较低.卫星直接入轨的示意图如图1所示.

图中点L、I分别为卫星的发射点和入轨点，σL、σS分别对应卫星发射轨道和预定轨道，βL为卫星发射段地心角，所对应的时间tL为卫星发射段飞行时间.当卫星采用直接入轨方式入轨时，卫星的入轨段地心角与入轨时间与发射段地心角和发射段飞行时间相等.

直接入轨过程中当发射轨道与预定轨道共面时，与非共面相比由于在入轨点不需要进行轨道面的调整，此时发射段消耗的能量将显著减少，所以对于直接入轨的卫星一般其发射轨道与预定轨道处于同一平面内.对于发射轨道与预定轨道共面的情况，根据发射轨道是否与预定轨道和地球表面相切而又分为：单共切入轨和双共切入轨(图2).

单共切入轨中，发射轨道的远地点与预定轨道在入轨点I处相切，在发射点L处，发射速度矢量与当地水平面的夹角Θ为发射速度倾角，当发射速度倾角给定的条件下，所有发射轨道中，单共切轨道最省能量.双共切入轨中，发射轨道的近地点与地球表面在发射点L处相切，远地点与预定轨道在入轨点I处相切.此时发射段地心角βL=π,与单共切入轨相比由于双共切入轨对应的发射段地心角大于单共切入轨，所以双共切入轨在快速响应能力上比单共切入轨差，由于直接入轨的卫星其预定轨道通常离地面较近，不管是采用单共切入轨还是双共切入轨，发射轨道的半长轴都相差不大，导致其消耗的能量也较为接近，综合考虑发射段的时间和能量，在快速响应任务中普遍采用单共切入轨.单共切入轨中发射段飞行时间的计算方法如下[7]：

在发射点和入轨点处有：

(3)

式中fL、fI分别为发射点和入轨点在发射轨道上的真近点角，且fL=π-βL、fI=π，ρ为发射轨道的半通径，a0为预定轨道的半长轴.通过式(3)可以求得发射轨道偏心率eL

(4)

发射点偏近点角：

(5)

发射点平近点角：

ML=EL-eLsinEL

(6)

发射轨道半长轴：

(7)

卫星入轨时刻：

(8)

其中,tL0为发射时刻，当发射段地心角βL和预定轨道半长轴a0已知的条件下，便可以根据上述方程求得发射段飞行时间tL.

(2)间接入轨

与直接入轨相比，间接入轨最大的区别在于增加了自由飞行段，这种入轨方式一般用于对卫星入轨相位要求较高的空间任务中，例如空间交会、星座组网等.间接入轨又分为调相入轨、转移入轨、滑行入轨等多种方式，其中以调相入轨最为常见[8].

调相入轨与转移入轨相似，调相入轨过程中卫星先经历发射段进入调相轨道，然后由调相轨道进入预定轨道.调相入轨又分为低轨调相入轨和高轨调相入轨(图3)，低轨(高轨)调相入轨中卫星S在I处施加冲量进入比预定轨道低(高)的调相轨道，然后在调相轨道上运行一圈或数圈之后，再在I处施加冲量进入预定轨道.此时未进入调相轨道的卫星S′在预定轨道上运行相同的时间后，其站位位于卫星S之后或之前.

这一过程中，位于初始位置的卫星在转移轨道上等待的圈数为Ntra,位于目标位置的卫星在原始轨道上运行的整圈数为Norg,完成相位调整所需要的总时间为tM,有：

(9)

式中a0、aM表示原始轨道和调相轨道的半长轴，θ表示从初始位置沿着卫星在轨道上的运行方向到目标位置所转过的角度.

调相入轨中，卫星先后经历发射段和相位调整段，βL、2kMπ为各阶段所对应的地心角，tL、tM为各阶段所需要的时间，卫星的入轨时间为ti:

(10)

1.3 响应时间

响应时间是快速响应任务的主导量和关键参数，受卫星发射方式、发射地点、入轨方式等多种因素共同影响[9].通过对快速响应任务中卫星的发射和入轨方式的分析，确定快速响应任务中响应时间的构成如图4所示.

图中,tr、tw、ti分别为发射准备时间、发射等待时间、入轨时间，各时间段的起止时刻如图所示.快速响应卫星的响应时间tresp:

tresp=tr+tw+ti

(11)

1.4 预定轨道的描述方式

快速响应任务中对预定轨道进行设计时，本文仅考虑偏心率为0的近地圆轨道.在对预定轨道进行描述时，选用轨道半长轴a0、轨道倾角i0、升交点赤经Ω0、入轨点纬度幅角μI4个参数进行描述.其中入轨点纬度幅角μI的求解方法如下：

假设在轨运行的卫星在tB时刻位于轨道上的B点，且B点的赤经和赤纬分别为αB、δB，纬度幅角为μB，轨道在天球上的投影如图5所示.

在球面直角三角形MBN中有：

sinδB=sinμBsini

(12)

tan(αB-Ω)=tanμBcosi

(13)

若B的地理经纬度为(λB,φB)，则有：

(14)

当采用发射轨道与预定轨道共面的方式入轨时，发射轨道与预定轨道在天球上的投影重合，对于发射点L由式(12)～(14)可以得到：

sinφL=sinμLsini0

(15)

(16)

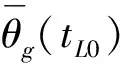
μI=μL+βL

(17)

所以当发射点地理位置(λB,φB)和发射时刻tL0已知的情况下，发射轨道与预定轨道共面时，可以根据预定轨道的轨道倾角i0、升交点赤经Ω0和发射段地心角βL求得卫星入轨点I处的纬度幅角μI.

2 基于快速响应的重构构型设计优化模型

2.1 优化变量

借助快速响应卫星来增强和恢复受损星座的服务性能时，发射的快速响应卫星数以及快速响应卫星预定轨道的轨道参数，直接决定了重构后的星座性能和完成快速响应任务的时间.此外，快速响应卫星的发射方式和入轨方式也影响了优化模型中变量的种类和数量.不同发射方式所对应的发射等待时间不一样，而且发射点的地理经纬度也会影响预定轨道的轨道参数.

综上，在基于快速响应的重构构型设计中所涉及的优化变量有：

2.2 约束条件

对在轨卫星进行相位机动，来调整星座的空间构型时，追求的一般是在任务要求的时间内以消耗能量最少为目的将卫星调整至目标位置，但是对于快速响应任务而言，利用调相入轨的方式调整卫星入轨时的相位角时，追求的则是在完成相位调整任务的前提下最大程度的缩短相位调整的时间.

假设目标位置的相位角为μt，初始位置的相位角为μ0，从初始位置沿着卫星在轨道上的运行方向到目标位置所转过的角度为Δμ:

(18)

相位调整过程中，目标位置的卫星在预定轨道上运行的时间与初始位置的卫星在调相轨道上运行的时间相同：

(19)

且有：

(20)

式中，k0为目标位置的卫星在预定轨道上运行的整圈数，在快速相应任务中当a0确定的条件下，要使得相位调整阶段所消耗的时间最短，则必须保证在式(19)、(20)成立的条件下，k0取得最小值.联立式(20)、(21)可以得到：

k0=

(21)

确定k0之后，根据式(21)求得调相轨道的半长轴aM以及卫星在调相轨道运行的圈数kM.

2.3 目标函数

本文在对重构构型进行优化时仅考虑重构后的星座性能(目标区域的平均GDOP值[10-11]，记为Gave)以及快速响应任务的响应时间.对于单颗卫星而言，任务响应时间tresp为任务下达开始到快速响应卫星进入预定轨道截止所经历的时间；对于多颗卫星而言，任务响应时间Tresp为任务下达开始到所有快速响应卫星都进入预定轨道截止所经历的时间：

(22)

所以目标函数F(x)为：

minF(x)=(Gave,Tresp)

(23)

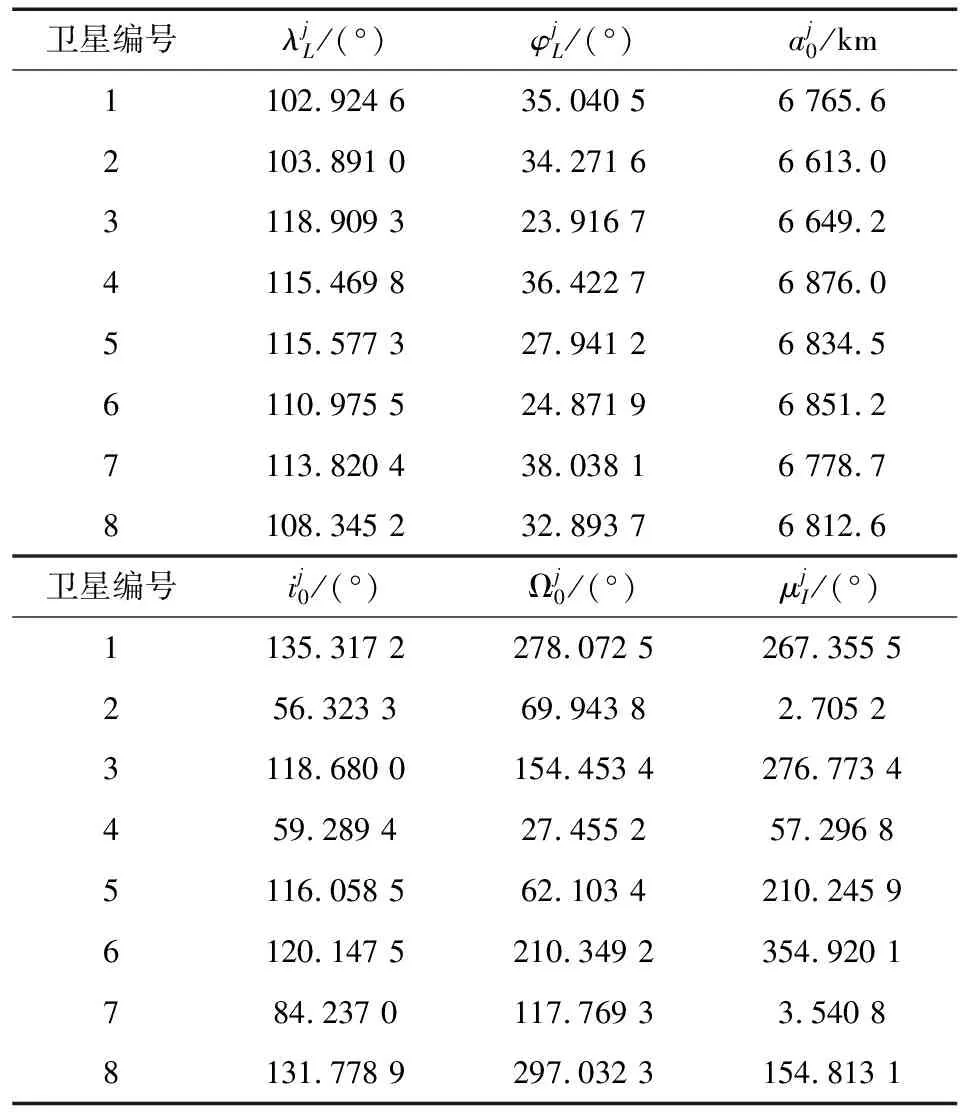
此外，当发射轨道与预定轨道共面时，由于受发射点地理位置的限制，当发射点的地理纬度为φL时，此时该点所能发射的快速响应轨道的轨道倾角i∈[φL,π-φL]，所以在优化过程中，如果快速响应卫星发射点的地理纬度φL>i或者π-φL

3 算例分析

对基于快速响应的重构构型设计优化模型进行求解时，采用NSGA-Ⅱ算法[12-13].关于NSGA-Ⅱ算法的操作流程，以及多目标优化问题下不同个体的评价机制在此不再赘述.本节主要就快速响应轨道参数的编码方式进行介绍，并对基于快速响应的导航星座重构构型优化模型进行仿真计算和对比分析.

3.1 快速响应轨道参数的编码方式

基于快速响应的导航星座构型重构是一个维数可变的优化问题，快速响应卫星的数量直接决定了优化变量的个数，但快速响应卫星数本身作为一个待优化的变量，其取值也是不确定的.本文对快速响应卫星的轨道参数采用如图6所示的双层编码方式：

Sj(j=1，2，3,…,n)为快速响应卫星的状态函数，其中n为一次快速响应任务中所能发射的最大卫星数.重构过程中所发射的快速响应卫星数：

(24)

3.2 算例描述

以建成后的北斗卫星导航系统为对象，假定星座中的MEO卫星全部失效.现通过发射快速响应卫星来对受损星座进行重构,以实现短时间内快速提升受损星座对目标区域的服务性能.快速响应卫星采用机动发射与定点发射相结合的方式，发射范围取为{(λL,φL)|100°≤λL≤120°,23°≤φL≤40°}，并忽略发射准备所需要的时间即tr=0，快速响应卫星的轨道高度范围取为[200 km,500 km]，发射轨道地心角所能取到的最小值βLmin=10°，一次快速响应任务中所能发射的最大卫星数n=8，且快速响应卫星均采用调相入轨的方式进入预定轨道.

仿真时间为[1 Jan 2020 00:00:00.000 UTCG]～[8 Jan 2020 00:00:00.000 UTCG]，目标区域为亚太区域(东经55°～东经180°，南纬55°～北纬55°)，考虑到快速响应卫星的轨道高度较低，受大气阻力摄动的影响较大，所以在分析重构后星座对目标区域的服务性能时，除了考虑地球扁率摄动外还应该考虑大气阻力摄动.地面网格分辨率为2°×2°，NSGA-Ⅱ算法中的初始参数设定：初始种群规模为150，最大迭代次数为200，上层染色体与下层染色体的交叉、变异概率分别为0.9和0.09.

3.3 仿真计算

当种群进化至200代时，将最后一代种群中的个体作为该问题的Pareto前沿，如图7所示.

该响应策略下每颗快速响应卫星的响应时间Tresp如图8所示.

表1 (Gave,Tresp)=(3.900 0,14.162 7)所对应的响应策略Tab.1 Response strategy corresponding to (Gave,Tresp)= (3.900 0,14.162 7)

在表1中所对应的重构策略下，对受损星座重构前后Gave随时间和空间的分布情况进行对比，如图9、图10所示.仿真结果显示：重构前Gave随时间的波动范围为[4.863 0,5.064 3]，而重构后Gave随时间的波动范围为[3.127 9，4.643 8]；重构前Gave≤6 的网格数为83.11%，重构后Gave≤6的网格数为94.60%.经过重构受损星座对目标区域的服务性能得到了有效的提升.

4 结 论

本文借助地面快速响应的方式对受损后的导航星座进行重构，建立快速响应卫星发射、入轨过程以及响应时间的数学模型，和基于快速响应的重构构型优化设计模型，并通过仿真算例证明了该方法的有效性.但本文仅分析了利用地面快速响应的方式来提升和恢复受损导航星座性能的方法，除此之外，利用在轨卫星的轨道机动和借助其他导航星座形成组合导航系统来增强受损导航星座性能的方法[14-15]也具有一定研究价值，而这对增强我国空间系统的弹性、可靠性面具有重要的战略意义.