基于模糊理论和逆推算法改进均值生成函数的短期风速预测研究*

王为国，窦震海，刘小煜，刘伟，申晋

(1.山东理工大学 电气与电子工程学院，山东 淄博 255000;2.青岛理工大学 琴岛学院，山东 青岛 266106)

0 引 言

风电在给我国的环保事业、能源结构调整等方面带来利益的同时，也伴随着一些问题的出现[1-2]。风电作为一种间歇性能源，风速、风量的不可控性会使风电输出缺乏稳定性。不稳定的风力发电上网，使电力系统运行中的不确定性因素增多，这对电力系统的供需平衡与安全稳定运行提出了新的挑战[3]。

风电场功率预测的准确性主要取决于短期风速的预测精度，由于风速本身既存在着规律性的变化趋势，又具有因不确定性因素造成的随机波动，使得对其进行精确预测具有较大的难度[4-5]。在目前研究中，短期风速预测模型主要有时间序列法和智能算法，而每种方法对风速预测的绝对平均误差一般在25%～40%之间，还未达到电力系统所要求的满意程度[6]。时间序列模型是对风速等随机变量进行拟合建模的一种常用方法，持续法是其中最简单的方法，更高级的时间序列模型主要有自回归滑动平均(ARMA)、卡尔曼滤波等模型[7]。智能算法是预测精度较高的风速预测方法，主要包括神经网络、灰色模型、支持向量机等方法[8]。时间序列分析建模几乎完全基于原始数据进行预测，算法过于简单；智能算法与黑匣子原理相似，虽然精度较高，但推导具体的预测解析式比较困难，并且在实际建模过程中需要大量的样本数据。从目前研究成果看，因为风速兼有随机波动性和趋势性，加大了短期风速预测的难度，如何提高风速模型的预测精度仍然是一个亟待解决的问题。

文献[9]尝试将在气象学中应用较为广泛的均值生成函数模型运用到风电场的短期风速预测中，该方法有效地提高了风速预测模型的精度，对序列极值的跟随性也较好，但在构造均值生成函数过程中，因为周期算法的缘故常导致样本序列尾部数据的作用失效。并且从预测经验及物理意义上考虑，越靠近起报时刻的数据值包含对预测有用的信息越多，对预测越有价值，以均值生成函数为基函数建立的风速预测模型并没有考虑到这些因素，预测精度仍有待提高。针对上述研究现状，文中在深入剖析均值生成函数预测模型特性的基础上，对均值生成函数模型进行了改进和完善，建立了一种基于模糊均生函数(Fuzzy Mean Generating Function, FMGF)[10]和最优子集回归(Optimal Subset Regression, OSR)[11]相结合的短期风速预测模型。通过定量对比表明，文中所构建模型能够获得较好的预测效果，有效地提高短期风速预测精度。

1 均值生成函数的原理

均值生成函数的基本思路是将原始时间序列样本转化为一系列可反映不同周期性质的基函数，然后根据不同情形选用不同的建模方案，既能够向外多步进行预测，又能实现对极值的较好预测。其基本原理如下：

设一组样本序列：

x(t)={x(1) ,x(2),…,x(n)}

(1)

式中n表示样本序列所包含的元素数量。接着，由式(2)定义其均值生成函数：

式中i=1,2,…,l; 1≤l≤m;nl=INT(n/l);m=INT(n/2)；INT为数据整数。

易知，均值生成函数处理样本序列的思路是先按照一定的间隔挑选样本，然后计算其平均值，从而得到一组周期函数。接着，将一个周期上的均值生成函数延拓至整个区间：

式中i=1,2,…,n；mod为同余算子。

于是得到均值生成函数的延拓矩阵：

F=(fi,j)n×l,fi,j≡fl(t)

(4)

式中n×l为矩阵阶数。

2 基于改进均值生成函数的短期风速预测模型

2.1 模糊集隶属度的构建

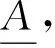
为叙述方便，令起始预测时刻为tn，对时刻点tn+1,tn+2,…,tn+q进行预测。在马尔柯夫预测中，只有tn时刻的数据对预测有用，tn以前的数据不发挥作用。若样本序列符合马尔柯夫特点，则隶属度函数可定义为：

AM=0/u1+0/u2+…+1/un

(6)

式中AM为具有马尔柯夫特点的隶属度函数。

若从统计学角度考虑，则把样本序列X(1),X(2) ,…,X(n)等概率对待，则隶属度函数定义为：

AS=1/u1+1/u2+…+1/un

(7)

式中AS为统计学意义下的隶属度函数。

在实际问题中，既不能舍弃过多以往的信息，又要使近期观测值对预测起到较大作用。因此，设计了随观测值的远近以指数形式递减的隶属度，即：

式中β依据对过去数据的重要性提前给出，一般为0.01.

若样本序列具有周期性，则令隶属度为：

式中l为周期长度；r为由经验提前确定的常数。

若既考虑观测值随起报时刻远近效用逐渐下降又要体现周期性，则令隶属度为：

(10)

式中β,l,r表示的含义同上。

2.2 均值生成函数的改进原理

基于均值生成函数的时间序列预测模型与自回归滑动平均、卡尔曼滤波、指数平滑等传统时间序列模型相比，解决了随预测期延长预测值趋于平均化的问题，并可以向外推多步进行预测，对极值的拟合预测效果也较好。可是，这些建模方案仍不完善，文中在传统均值生成函数预测模型的基础上，对其进行了改进和完善。

具体改进如下：

(1)从预测经验及物理意义上考虑，距离起报时刻越近的观测值包含对预测有用的信息越多，对预测越有价值，而以均值生成函数为基函数建立的预测模型忽视了这些因素。由于模糊均生函数计算方法能够有效体现出近期的样本数据对预测值的较大影响，并能够充分利用样本数据中所隐含的有用信息，自提出以来，该理论在短期负荷预测、降水量预测、天然径流预测、飞行事故率预测等领域已取得成功应用。而目前尚未见使用模糊均生函数计算方法来进行风电场短期风速预测的报道，因此文中尝试用随指数形式递减的隶属度构造模糊均生函数，进而将其引入到短期风速预测研究中，以提高风速预测的精度；

(2)由于均值生成函数是由样本数据按照一定的间隔计算均值而获得的周期函数，因此在生成均值生成函数过程中，常出现时间序列的尾部样本值无法发挥作用的问题。而大量实验表明，时间序列的尾部样本值在整个实际预测过程中具有重要的意义。为了解决这一问题，文中引入了文献[11]推导出的逆推算法，使用该算法对均值生成函数的定义过程进行了完善，以使得尾部样本值在均值生成函数延拓序列中的作用能够实现。

上述过程在保留均值生成函数预测模型的主要优势(多步预测和极值预测效果好)的基础上，进一步考虑了近期数据对风电场短期风速预测结果的较大影响，并妥善解决了传统预测模型中周期算法的尾部样本值失效的问题，为如何预测兼有随机波动性和趋势性的短期风速提供了一条新思路。

2.3 最优子集回归模型的短期风速预测

针对风速兼有随机波动性和趋势性的特点，文中在改进均值生成函数构造原理的前提下，将其与最优子集回归模型相结合，建立基于FMGF-OSR的短期风速预测模型。改进模型的具体建模流程如下：

2.3.1 推导时间序列样本的FMGF延拓序列

推导步骤如下：

步骤一：为了充分挖掘以往信息，又能使近期数据对数值的预测发挥较大作用。因此，文中选用了随观测值的远近以指数形式递减的隶属度，即:

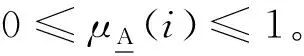
步骤二：对于式(2)，根据指数形式的隶属度和逆推算法构建FMGF如下：

(12)

式中Rl=n-nl·l;i=1,2,…,l; 1≤l≤m;nl=INT(n/l);m=INT(n/2)；l为函数的周期；INT为数据取整；Rl为样本总项n的余项。可见，在定义FMGF过程中通过逆推算法调整了处理样本序列的顺序，即从样本序列的第Rl+i项开始，一直计算到最后一项。通过改进FMGF定义过程，确保了时间序列的尾部样本值在各周期所对应的FMGF序列中均能发挥作用。

步骤三：对FMGF序列进行周期延拓：

式中i=1,2,…,n；mod为同余算子。即可得到FMGF的延拓矩阵：

F=(fi,j)n×l,fi,j≡fl(t)

(14)

步骤四：为了拟合原序列的高频分量，对原序列分别进行两次差分处理：

x(1)(t)={Δx(1) ,Δx(2),…,Δx(n-1)}

(15)

x(2)(t)={Δ2x(1) ,Δ2x(2),…,Δ2x(n-1)}

(16)

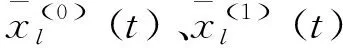
步骤五：为了对原始序列中的变化趋势进行拟合，将一阶差分周期延拓序列进行累加处理：

式中fl(3)(1)=x(1)；t=2,3,…,n；l=1,2,…,m。

2.3.2 双评分标准CSC (Couple Score Criterion)

由2.3.1节可以得到约4m个FMGF延拓序列，每个序列将作为预测模型的一个预测因子。因为短期风速样本数据具有随机波动性和趋势性的特点，所以文中使用同时考虑趋势和数量的双评分标准[12]进行预测因子的筛选：

CSC=S1+S2

(18)

式中S1表示数量评分；S2表示趋势评分。

数量评分定义为：

式中R2表示复相关系数；n表示风速序列长度；QK和QX分别表示残差平方和、总离差平方和。

趋势评分定义为：

S2=2[R1+(n-1)·ln(n-1)-R2-R3]

(20)

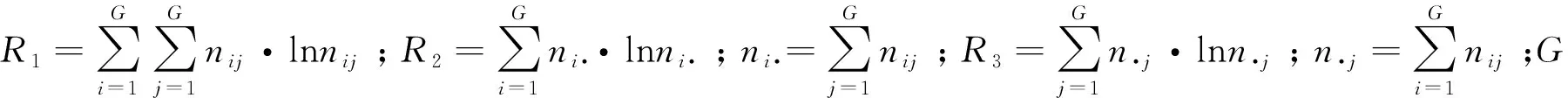
2.3.3 粗选预测因子

因为预测模型中含有大约4m个FMGF延拓序列，若把它们都当作自变量，并按不同的自由组合与因变量建立回归方程，这将导致计算量偏大，也没有这样进行的实际意义。因此，文中首先使用双评分标准对上述变量进行筛选，剔除CSC值较低的预测因子。

2.3.4 精选最优子集

将生成的2h-1个子集分别进行多元线性回归计算，并再次计算所有回归结果的CSC值，然后从2h-1个子集中挑选得到CSC值最大的子集，即获得风速预测模型的最优子集。

2.3.5 建立短期风速预测模型

若最优子集回归方程由k个自变量组成，则得到的基于FMGF-OSR的短期风速预测模型为：

若要进行q步的风速预测，将式(21)中的FMGF序列fi(t)(i=1,2,…,k)仿照式(13)完成q步延拓，然后将其代入短期风速预测模型，即可完成对风速值的预测。

3 算例分析

3.1 样本数据

文中实验样本来自中国北方某风电场2017年2月份某一天的风速值，按照10分钟级的时间尺度对风速进行采样，一共获得144个数据，实测风速数据如图1所示。考虑到仿真的复杂性，文中截取了前4 h的风速值，并将获得的24个实测值作为原始时间序列样本，然后采用文中所构建模型对其后1 h的风速值进行预测。为比较文中提出的预测模型的优越性，文中同时采用了均值生成函数-最优子集回归模型(MGF-OSR)、均值生成函数-主成分回归模型(MGF-PCA)和经典的自回归滑动平均模型(ARMA)对未来风速值进行预测。其次，为了突出对MGF-OSR模型的改进之处，文中将FMGF-OSR模型与MGF-OSR模型的建模流程进行了对比，如图2所示。

图1 原始风速信号Fig.1 Original wind speed series

图2 两个模型的建模流程Fig.2 Flowcharts of two models

3.2 误差评价函数

为了有效和全面地对各预测模型的准确率进行量化评价，误差评价函数选用相对误差(Relative Error, RE)、平均绝对百分误差(Mean Absolute Percentage Error, MAPE)和均方根误差(Root of the Mean Squared Error, RMSE)，其表达式分别为：

3.3 预测效果分析

使用MATLAB编程进行仿真，分别采用4种预测模型得到的风速预测值如图3所示。

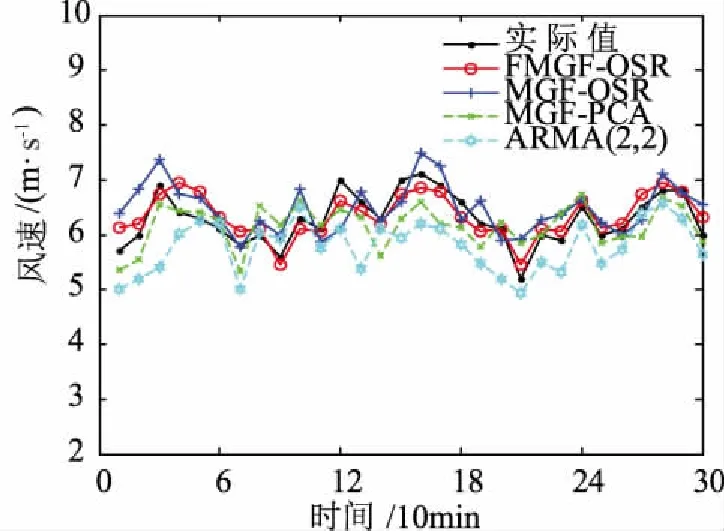
图3 4种预测模型的风速预测结果Fig.3 Wind speed prediction results by four models

由图3可见，根据FMGF-OSR模型得到的风速预测曲线与实际的风速数据更为接近，预测精度最高。下面进一步结合误差评价函数来详细说明文中所建立预测模型的有效性和优越性，依据式(22)～式(24)得到各种模型的预测误差结果如表1和表2所示。

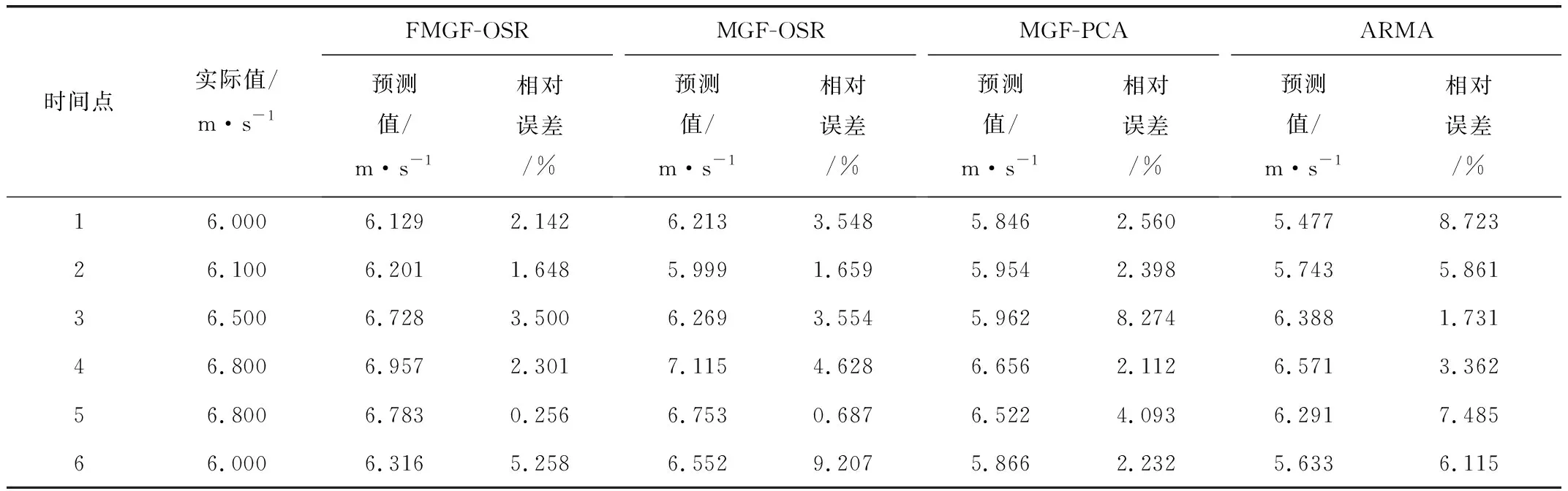
表1 风速预测结果比较Tab.1 Comparison of wind speed prediction results

表2 各预测模型的误差对比Tab.2 Errors comparison of different prediction models

由表1和表2可知，文中预测模型将实际风速值与预测值之间的相对误差基本控制在2.5%左右，表明该预测模型的有效性。同时通过3种典型的预测误差量化指标，可知文中提出的FMGF-OSR模型较MGF-OSR模型、MGF-PCA模型、ARMA模型均明显更优。这是由于FMGF-OSR模型在保留MGF-OSR模型的优势基础上，结合模糊理论和逆推算法对其进行了进一步的改进和完善，使得改进后的模型能够充分挖掘原始数据中隐含的有用信息，对原始数据中的高频分量及趋势性都进行了较好地拟合，有效降低了风速预测的误差。在文中实际算例仿真中，推导出的风速预测模型方程包括1个原始序列、1个一阶差分序列和2个累加延拓序列的模糊均生函数序列。

4 结束语

文中提出了一种基于模糊理论和逆推算法改进均值生成函数的短期风速预测模型，该模型有效解决了传统均生函数预测模型中由于周期算法导致的邻近数据无法发挥作用的问题，也使得距离预测点越近的风速值对实际预测起到的影响越大，并引入了能够体现不用周期特性的模糊均生函数序列作为预测因子，这对极值的拟合和预测都取得了比较理想的效果。实例表明，与常用的几种风速预测方法相比，该模型的风速预测误差基本控制在2.5%左右，其有效性和优越性均得到了验证，具有较高的实际应用价值。