固定式光伏发电组件最佳倾角的聚类分析方法*

迟福建, 葛磊蛟, 洪博文, 李盛伟, 高毅, 张东

(1.国网天津市电力公司，天津 300010； 2. 天津大学 电气自动化与信息工程学院，天津 300072；3. 国网能源研究院有限公司，北京 102209； 4. 国网天津市电力公司经济技术研究院， 天津 300171)

0 引 言

集中式光伏发电系统主要由光伏发电板阵列、逆变器、汇集与送出单元及相关的控制系统等组成，决定其光电转换效率和输出功率、发电量的重要关键点之一是光伏发电板阵列的方位角及倾斜角。当前光伏发电板阵列的安装方式，一般分为追踪式和固定式两种，其中，追踪式是通过安装方向调节装置，可根据太阳位置随时调整光伏板受光面，但是初期投资成本相对较大，在大型集中式光伏系统应用较少；固定式光伏发电阵列是根据场站位置计算出相对较好的受光面后固定不动，具有投资小、使用寿命长、运维工作量少等特点，但是发电效率，与追踪式光伏发电阵列相比会有所减少。因此，在大型集中式光伏系统建设过程中，需要综合考虑地域环境、建设和运营成本及光电转换效率等多因素，科学确定固定式光伏发电阵列的方位角和倾斜角，从而选择最佳受光面，达到最大的经济效益。

近年来，光伏发电技术发展迅猛，国内外学者们进行了一些研究。文献[1]基于综合价值提出了一种固定式光伏阵列朝向与倾角优化方法，较好的解决了不同方位与光伏阵列朝向出力差别之间的关系。文献[2]通过对区域内不同倾角光伏阵列出力的实测数据进行对比分析，获得最佳倾角，是一个较为典型现场实证案例分析。文献[3]通过5个不同的光伏电站实际工程案例，对武汉地区的光伏组件安装倾角进行了实证分析，获得了较好的效果。文献[4]从光伏阵列获得的辐照量入手，构建了光伏最佳倾角的优化模型，并进行了求解。另外，一些学者对光伏的特性分析[5-8,16]、最大出力跟踪[9]、出力预测[10]等方面，进行了一些研究。

结合光伏电站所在地区的经纬度、地域环境等实际情况，广泛收集国内外光伏研究的知名网站光伏组件发电量及光伏阵列安装参数等数据，以集中式光伏电站全年获得有效辐射量为目标，即整体经济最优为目标，提出了基于聚类分析的光伏发电组件最佳受光面模型，实现对发电光伏组件受光面的倾斜角求解，以北方某174 MW光伏电站案例为例，并将计算结果与PVsyst软件的计算结果进行对比分析，验证该方法的精确性。

1 固定式光伏发电组件的最佳倾角模型

一定容量的集中式光伏发电站实际出力大小受到地理位置、太阳辐照度、安装方式、环境温度及光伏板表面积尘等多种外部条件影响，一般难以用简单的数学模型精准描述，在工程应用中一般以光伏组件全年获得有效辐照量最大为基本目标，然后以尽可能最佳或者相对好的原则，选择光伏组件的安装倾角，从而实现光伏组件的全年整体经济最佳。

固定式光伏组件的年总辐射量Qs为：

Qs=Ds+Ss+Rs

(1)

式中Ds是年直接辐射量；Ss是年天空散射辐射量；Rs是年地面反射辐射量，因地表反射对太阳能硅电池发电影响较少，一般不予计算。

式中D0是太阳辐射常数，取1 367 W/m2;N是日系，即一年中从元旦算起的天数；τb是太阳直辐射系数；θ是太阳的直射角。

式中τs是太阳散射透明度系数；β是光伏板安装倾角；φ是光伏板的纬度;δ是太阳的赤维角；ω0是水平面日出、日落的时角。

从公式(1)～公式(3)中不难发现，固定式光伏发电系统的倾角选择应综合考虑太阳辐射的直射角和赤维角、光伏板的纬度、光伏板的安装倾角等多方面特性，但是一般的工程应用过程中，光伏电站区域地点选定后，认定其主要变化参数是光伏板的安装倾角β，为此，以全年光伏板获得的有效辐照量为目标值，建立固定式光伏板最佳倾角数学模型如下：

式中β为光伏组件的安装倾角；QT(β)为某一安装倾角下光伏组件的倾斜表面年辐照量；QT(β,i)为某一倾角下光伏组件倾斜表面第i个月的平均日辐照量；M(i)为第i个月的总天数。当然，在实际的工程应用过程中，固定式光伏组件之间相互遮挡、外界物体阴影等特定的安装条件，也会对光伏组件最佳倾角选择有一定的影响，但是由于工程条件场景过多而统一表述比较难，暂时未予深入考虑。

针对所构建模型，一年的太阳辐照是逐月连续变化的，且不同年、月差异性较大，是一个不均匀分布，已有的美国NASA气象网站、RETScreen等网站数据，由于所采用的分布算法不同，同一地区同一区域同一时间内的太阳辐射量数据也不近相同。于是，常出现相同的光伏组件最佳倾角模型和相同的光伏安装倾角，而由于不同的输入数据来源，获得的结果差异性比较大，因此考虑区域经纬信息，以美国NASA气象网站、RETScreen等多个网站数据和现场的实际量测采集数据为输入数据，应用聚类分析方法对光伏组件最佳倾角模型进行优化，实现更加精准的光伏安装倾斜角求解。

2 聚类分析法及计算流程

聚类分析方法是一种定量确定样本之间亲疏关系的多元分析方法[11-15],主要包括模糊聚类和直接聚类两大类方法。针对光伏组件最佳倾角模型的输入数据具有需求各异、特征不一等实际情况，拟应用模糊聚类分析方法对其进行聚类分析，主要的计算步骤如下。

2.1 数据标准化

同一地区的月太阳能辐照量，来源于不同的网站数据而具有不同的量纲，为了使不同量纲的数据均满足模糊矩阵的要求，实现将数据压缩到区间[0,1]，先对数据进行变换。

设样本域U={u1,u2,…,un}为被分类的对象，域中的每个元素ui均由m个数据组成，即第i个元素ui可表示为：

Ui={xi1,xi2,…,xin}, (i=1,2,…,n)

(5)

因此，原始数据域可写成矩阵的形式，即：

构建原始数据域矩阵U后，先进行标准差变换；如果标准差变换无法满足值域[0,1]要求，接着进行极差变换。

(1)标准差变换

矩阵U中的任意一个数据，进行标准差变换的公式如下：

式中i=1, 2, …,N；k=1, 2, …,m; 经过变换后，矩阵U中的每个变量均值为0，标准差为1，可消除量纲的影响，但有时不一定值域在[0,1]区间上,为此进一步进行极差变换。

(2)极差变换

矩阵U中的任意一个不满足需求的数据，进行极差变换，其变换公式如下：

式中k=1,2,…,N。

2.2 建立模糊相似矩阵

数据标准化完毕，为有效对样本域U间的数据相似程度进行分类，构建样本域U的数据相似程度统计量rij(i,j=1,2,…,N)，从而形成模糊相似关系矩阵R，其主要过程如下。

设样本域U={u1,u2,…,un}，其中，每个元素ui为一个样本，每个样本为m维向量，即，于是，建立U上任意两个样本之间的相似关系矩阵R，根据R值对样本域进行分类，其任意元素rij可表示为：

rij=R(ui,uj)

(11)

rij的计算方法，根据不同的聚类方式，计算方法不同,拟采用方法为有平均值距离、平均距离、最大距离和最小距离等。

平均值距离：

dmean(ui,uj)=d(fi,fj)

(12)

平均距离：

最大距离：

dmax(ui,uj)=maxd(xik,xjk)

(14)

最小距离：

dmin(ui,uj)=mind(xik,xjk)

(15)

式中fi,fj分别为样本域U中的元素ui,uj的平均值;xik,xjk分别为样本域U中元素ui,uj的第k个指标的具体数值。后续将根据平均值、平均距离、最大距离和最小距离等设定相对应的阀值，对数据进行分类。

2.3 聚类分析与应用

建立模糊相似矩阵R后，分别导入光伏发电各个网站的月辐照量数据，采用模糊C均值聚类法对其进行聚类分析。

该算法的基本原理是把来源于不同网站的光伏电站地区N个月辐照数据xk(k=1, 2, …,n)，分为c个模糊类，然后求取每类的聚类中心，使得类内加权误差平方和函数达到最小，其目标函数的形式为：

式中 表示第k个网站的隶属于第i个聚类中心的程度；Pi为模糊类的聚i类中心；dik为第k个聚类中心与第i个网站输入数据之间的欧几里德距离；m∈[0,2]为一个加权指数。参照目标函数，依据聚类准则，可构造拉格朗日函数：

式中λk(k=1，2，…，n)是等式约束式的拉格朗日乘子。然后对上式所有输入参数求导，即可得到目标函数为最小的必要条件为：

针对以上的最优化问题，以式(18)和式(19)两个必要条件为依据，最佳模糊分类矩阵ui和聚类中心Ci的计算算法如下：

(1)基础参数初始化：根据实际工程情况和所处地域，赋予分类数c、待分元素的行数m和列数n以及循环误差判别限值ε等初始值；

(2)给定c个聚类中心的初始值；

(3)计算隶属度μij；

(4)计算聚类中心坐标ωi′；

(5)根据误差判别限值ε，若‖ωi′-ωi‖≤ε，则停止循环，否则令ωi=ωi′，跳到步骤(3)，如此循环进行。

3 工程案例分析

在华北某174 MW大型光伏电站设计过程中，以美国NASA气象网站、RETScreen、国家气象中心网站和实际现场测试的太阳月辐照数据为基础输入数据，应用基于聚类分析方法对光伏发电组件最佳倾角进行求解，并应用PVsyst软件进行进一步的校核。

3.1 输入数据

(1)光伏阵列的方位角

光伏组件方阵的方位角是方阵的垂直面与正南方向的夹角。一般在北半球，太阳电池组件朝向正南(即方阵垂直面与正南的夹角为0°)时，太阳电池组件的发电量是最大的。本工程位于北半球，光伏阵列应朝向赤道方向(即正南方)安装，故确定光伏阵列的方位角为0°。

(2)光伏阵列的经纬度和时角

针对华北地区某174 MW大型集中式光伏电站所处地区，根据《光伏发电电站设计规范》查表可知自然属性及技术参数，如表1所示。

表1 项目所处地域的基本参数Tab.1 Basic parameters of the area in project

(3)不同月辐照数据

项目所处区域，从美国NASA气象网站、RETScreen网站和国家气象中心，以及实际现场测试的太阳月辐照数据，如表2所示。

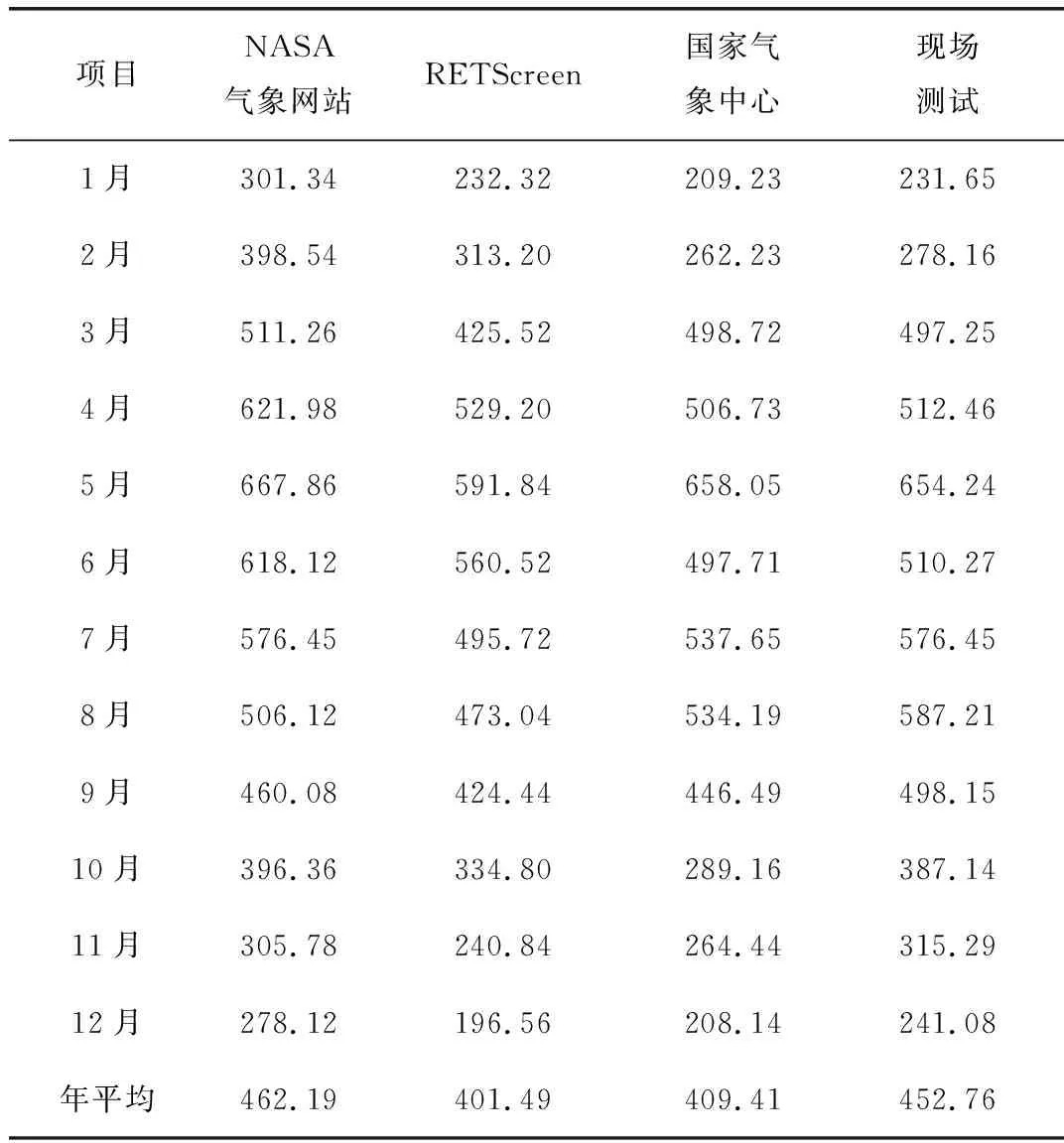
表2 太阳月辐照数据Tab.2 Solar radiation data in months

3.2 计算结果

将以上的基础计算所需数据，收集整理后，按照第二章的计算方法，经数据标准化、建立模糊相似矩阵及聚类分析后，得出不同倾角条件下该项目年平均发电量，结果如表3所示。

从表3不难发现：

(1)根据计算结果，在项目场址处、方位角正南条件下，30°倾角下光伏组件方阵面上的年发电量最大，为448 389.4万千瓦时，即此倾角下所捕获的年总辐射最大。36°倾角下相对发电量最小为446 448.3万度，最大与最小相比，相同地点安装倾角不同，光伏组件年多发电量为1 841.1万千瓦时；

表3 不同倾角情况下174兆瓦光伏组件年平均发电量(万千瓦时)Tab.3 Average generating capacity of 174MW PV module under different slit angles

(2)针对聚类分析方法而言，项目相关的数据种类和数据量越丰富，聚类分析的结果会与工程实际运行情况有较好的吻合度。但是实际工程的地形条件，例如外部物体阴影等因素，也会对运行产生较大影响。为此，在项目运行过程中，还应充分利用各种监测、监控设施，对实际的数据进行分类归集存储，然后进一步对所构建模型、聚类计算方法等进行完善和优化；

(3)利用光伏发电专业软件PVsyst，将表2的基础数据输入获得安装角30°时的发电量为448 176.5万千瓦时，与所提的聚类分析计算结果误差为1.35 %，完全符合工程应用要求，同时也验证了所提算法的可行性；

(4)同理，利用光伏发电专业软件PVsyst，将表2的所有基础数据输入PVsyst系统，分别获得安装角25°～30°时的发电量分别为4.464 214 7×109kWh、4.471 241 5×109kWh、4.472 157 4×109kWh、4.475 784 7×109kWh、4.478 543 6×109kWh、4.481 765 0×109kWh、4.476 852 1×109kWh、4.475 214 9×109kWh、4.471 253 6×109kWh、4.470 253 6×109kWh、4.466 523 6×109kWh、4.464 879 8 ×109kWh，与所提的聚类分析计算结果趋势基本一致，完全符合工程应用要求。

4 结束语

集中式光伏是近年来我国重要的新能源技术之一，发展非常迅猛。全国各地的各种工程项目也建设非常多，每一个工程不仅受限于地域、环境和投资成本等要素，也受限于组织、协调管理等情况，且不同工程所受限情况也不尽相同。所提出的固定式光伏发电组件最佳倾角的聚类分析方法，工程经济性方面入手，对于工程的前期设计验证，具有一定的指导意义，以期为集中式光伏的推广应用提供借鉴。