计及分布式电源输出特性的有源配电网重构方法*

徐嘉斌，吉兴全，公茂法

(山东科技大学，山东 青岛 266590)

0 引 言

随着新能源发电技术日趋成熟，分布式电源(Distribution Generation, DG)[1]在配电网中不断渗透，传统的配网分析方法已无法适用于当前含多种DG的复杂配电网。DG的广泛应用使得对配电网潮流计算[2-4]、故障恢复[5-7]以及优化重构[8-12]等问题的研究不得不考虑DG的影响。

在配电网的优化重构方面，DG的模型主要分为两大类：一类是确定性模型，即将DG视为恒功率输出或者功率可控的电源，并以负的负荷形式处理[8-10]。另一类是概率模型，即考虑DG出力的随机性，并通过概率统计的方式对DG的出力进行描述[11-12]。在确定性模型方面，文献[8]将DG视为恒功率输出，并采用混合粒子群算法对含DG的配电网重构问题进行求解；文献[9]在文献[8]的基础上改进了编码方式，采用基于独立环路的整数编码方式，减小了搜索空间，但在处理无效解时较为繁琐；文献[10]提出一种基于功率矩和邻域搜索的配电网两层重构算法，可以有效的提高配网重构的效率。在概率模型方面，文献[11]建立了基于机会约束规划的配电网重构模型，并使用改进蚁群算法进行计算；文献[12]在文献[11]的基础上，提出了基于无向生成树的并行遗传算法，实现了配电网重构模型的并行求解，对概率模型中计算规模较大进行了优化，提高了配网重构的效率。

上述文献中，无论采用确定性模型还是采用概率模型，均认为DG并联无功补偿设备，将DG看作为恒功率因数运行。在实际的配电网中，有些DG没有并入无功补偿设备，因此，这种DG恒功率因数模型仅能近似的描述部分DG的出力，忽略了电网结构以及节点电压改变对DG无功输出的影响，难以寻找到实际情况下最优重构方案。文献[13]把分布式电源等效成PQ和PV两种节点进行处理，虽然考虑到了节点电压的影响，但是DG种类繁多，仅分成两类具有片面性。为此根据DG的输出特性进行合理的分类，建立了一种考虑DG输出特性的通用模型，该模型结合DG在配电网中的实际情况，根据不同种类的DG分别考虑了电网结构和节点电压改变对DG出力的影响。并使用自适应烟花算法(Adaptive Fireworks Algorithm, AFWA)[14]分别对DG恒功率模型和所提DG模型的有源配电网进行重构比较，对比分析了两种模型下的重构方案，并与PSASP计算的潮流相对比，验证了所提DG通用模型能够更加真实地反映出DG出力情况，在该模型下的重构方法可以寻找到更加接近实际情况的重构方案。

1 分布式电源建模

随着新能源发电技术的不断发展，分布式电源种类繁多，可以根据其特性将其等效成不同类型的节点，大致分为PQ节点，PV节点，PI节点，PQ(V)节点四类。对于PQ节点类型的DG与负荷节点相同，在潮流计算时，等效为“负的负荷”，较为简单，故文中主要针对其它三类节点讨论[15]。

1.1 PV节点

采用恒电压控制方法的同步发电机以及通过电压型逆变器与电网并网的DG可以等效为PV节点。对于PV节点的处理，首先固定PV节点的无功出力，进而等效为PQ节点参与首次迭代。并计算在该固定无功功率下的电压，同时将计算电压与PV节点给定电压的差值等效为一个无功源。将网络中其他电源置零，计算仅有该无功源时的无功补偿电流，将此补偿电流叠加到节点现有负荷上参与迭代，这样就实现了PV节点的潮流计算[2]。通过补偿电流和节点电压可以计算出实际PV节点的功率输出，进而判断出该DG的实际无功出力。

考虑实际DG的逆变器无功功率输出是有上限的，当无功出力超过其最大值时，则将其转化为PQ节点来处理。逆变器实际的有功出力为P，最小功率因数为ρmin，则可输出的容量上限为：

此时，逆变器的最大无功出力为：

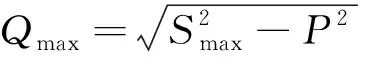
一般PV类型的DG不需要进行无功补偿，也不需要从电网中吸收无功，故其输出的无功最小值Qmin为0。若PV节点无功越限，则将其无功功率固定为最大值或最小值，进而转换为PQ节点参与潮流计算。

1.2 PI节点

有些DG通过电流型逆变器与电网并网，对于电流型逆变器，其输出的有功功率和流出的电流是恒定的，因此此类DG可等效为PI节点[16]，注入的无功功率Q可以计算为：

式中I为逆变器的恒定电流；P为恒定的有功功率；e和f为并网节点电压的实部和虚部。在潮流计算中，通过每次潮流计算得到的电压对无功功率Q进行更新，进而变为PQ节点参与下一次计算[17]。

1.3 PQ(V)节点

采用异步发电机发电的DG中，由于发电机吸收的无功功率受机端电压的影响，故将其看作为PQ(V)节点。

Q′=f(V)

(4)

式中Q′为异步发电机在输出有功功率为Pe时所需要吸收总的无功功率。

由于此类DG需要从电网吸收无功功率，为减少网络损耗，需要对其进行无功补偿，以确保功率因数在允许的范围内变化。一般采用并联电容器组的方式为其提供无功补偿功率。

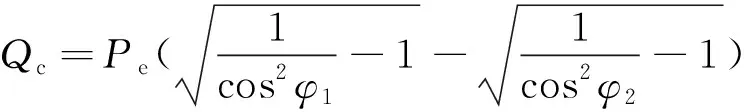
式中 cosφ1为无功补偿前的功率因数；cosφ2为系统允许的功率因数；Qc为功率因数由cosφ1提高到cosφ2所需补偿的无功功率。

令额定电压下并联电容器的单位容量为QNC0，采用无功功率过补偿方式，则实际投入电容器组数为：

[ ]表示向上取整，即取比该数值大的最小整数。

电容器组在电压V下的输出无功功率为：

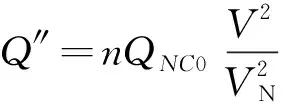
式中VN为额定电压。

则在机端电压为V，有功功率输出为Pe时，风机需要从电网吸收的无功功率为：

Q=Q′-Q″

(8)

如图1所示，当异步发电机组在有功输出为Pe且机端电压为V时，需要吸收总的无功功率Q′，对应的功率因数角为φ1；给系统提供无功功率Qc，可以将发电机组的功率因数提高到允许值cosφ2。在实际情况下，电容器组输出的无功功率为Q″(Q″≥Qc)，补偿后异步发电机组从电网中吸收的无功功率为Q。

图1 风机无功补偿示意图Fig.1 Schematic diagram of reactive power compensation for wind turbines

在潮流计算中，PQ(V)节点根据上一次计算出电压幅值V和给定的有功功率Pe计算出无功功率Q，转换成PQ节点参与潮流计算迭代[18]。

通过对分布式电源进行分类，将不同属性的DG划分为不同类型节点，采用前推回代法进行配电网潮流计算。

2 配电网重构的数学模型

将网络损耗最小作为配电网重构的优化目标：

式中Pi和Qi分别为支路末端的有功功率和无功功率；ri为支路i的电阻；Vi为支路i末端节点的电压幅值；T为配电网的支路集合。

约束条件：

(1)节点电压约束

(2)支路潮流约束

(3)配电网辐射状结构约束

g∈G

(12)

(4)功率平衡约束

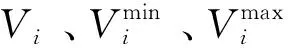
3 基于AFWA的配网重构

根据对标准测试函数的相关分析，烟花算法(fireworks algorithm, FWA)具有收敛速度快、搜索精度高、实现简单等优点[19]。在FWA中，主要有爆炸、变异、映射和选择4个操作。通过爆炸操作可以产生火花，通过变异操作提高火花的多样性，通过映射操作将越界的火花映射到可行域的范围内，通过选择操作挑选下一代烟花种群。爆炸操作是烟花算法的核心，对FWA起关键性作用。在基本的FWA基础上，采用了自适应的爆炸算子，根据已经生成的火花去计算最优烟花的爆炸半径，并结合精英-随机选择策略形成了自适应烟花算法[13]。该算法在FWA的基础上减少了参数，优化了计算量，提高了求解的速度和准确性。

3.1 自适应的爆炸算子

自适应的爆炸算子实质上是以当前获得的信息为最优烟花计算一个合理的半径。为方便叙述，定义第i次进化的烟花集合为X，其中最优烟花为xi，对所有烟花进行爆炸操作，产生火花集合S，在集合S中挑选一个适应度仅次于当代最优烟花xi的火花si，在集合{X，S}中挑选最优个体作为下一代的最优烟花xi+1。下一代最优烟花xi+1的半径为：

Ai+1=0.5(A+Ai)

(14)

式中Ai+1为第i+1次最优烟花xi+1的爆炸半径;Ai为第i次最优烟花xi的爆炸半径;A为计算的中间变量，d(xi,si)为xi到si的欧式空间距离;k为半径系数，通过对k的合理取值可以有效提高全局搜索的性能，通常取k为1.3，D为最大爆炸半径。

3.2 网络简化及编码

在使用智能算法对配电网重构问题进行寻优时，有可能会产生大量不满足连通辐射状约束的不可行解，进而影响搜索效率。使用独立环路的编码策略[20]，可以有效地降低解的维数，进而减小搜索空间。配电网重构实际上是寻找的一组开关组合，以尽量减少配电系统的网络损耗，保证配电网满足约束条件。在网络拓扑结构上的约束条件主要为：

(1)保障网络连通性，使其不形成孤岛;

(2)保障网络的辐射状结构，不形成环网。

根据条件1，可以对配电网进行简化，将环网之外的开关始终闭合，否则将形成孤岛。简化后的配电网仅含有环网内的开关。根据条件2，为保证系统不形成环网，需要在每一个环网中都断开一个开关。在AFWA中，取环路的数量为维度，每一个环网内的所有开关为该维度下的取值范围。进行以上操作大大减小了烟花算法的搜索空间，极大地避免了不可行解的产生。在处理不可行解时，根据图论中的连通度理论[21-22]，对其进行辨识和修正，修正后的解满足约束条件,算法流程图如图2所示。

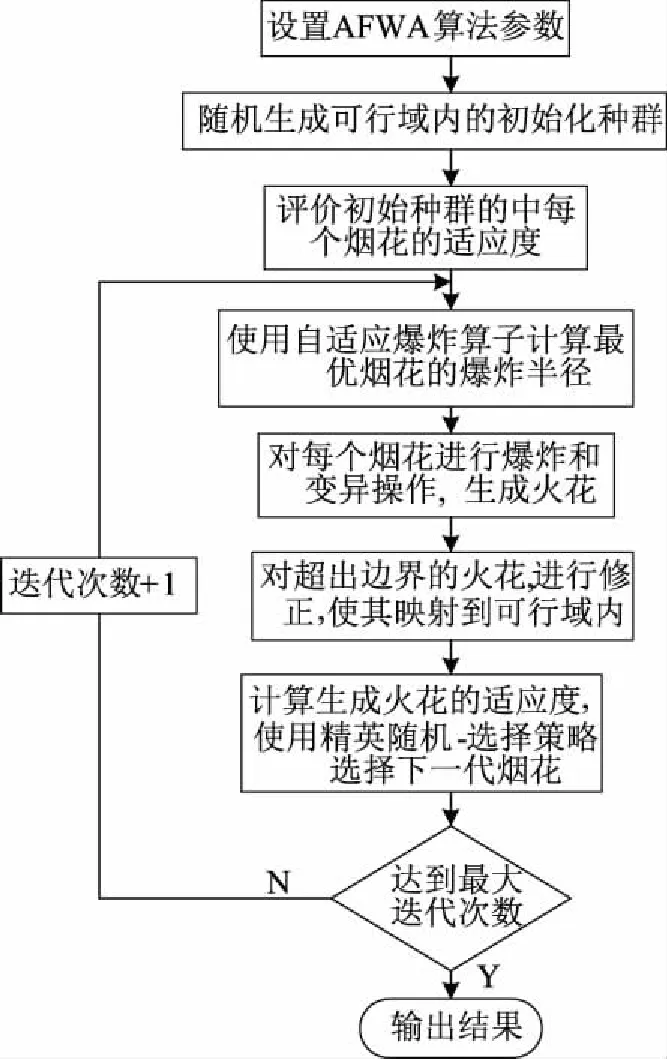
图2 AFWA流程图Fig.2 Flowchart of AFWA

4 算例分析

以图3所示的IEEE33节点系统[23]为例，并分别在7，11，19，24节点处加上不同类型DG。采用AFWA分别对所考虑DG属性的通用模型与文献[10]所述DG恒功率模型进行网络重构。

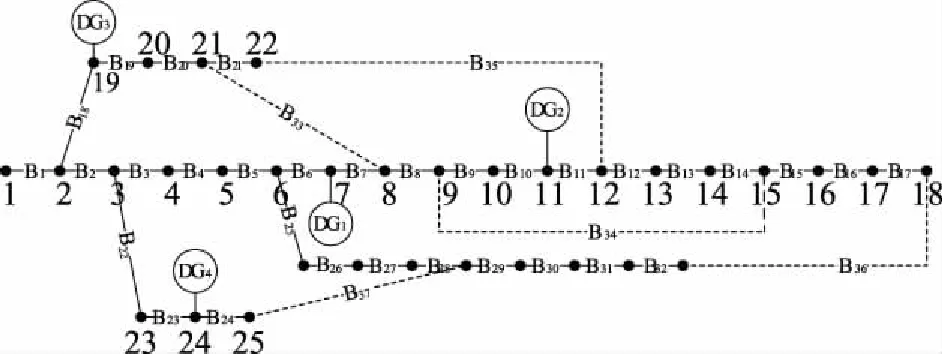
图3 含DG的IEEE33节点系统图Fig.3 IEEE33 node system diagram with DG

4.1 情况一

含DG的配电网各个DG的有功功率、DG类型以及接入点如表1所示。

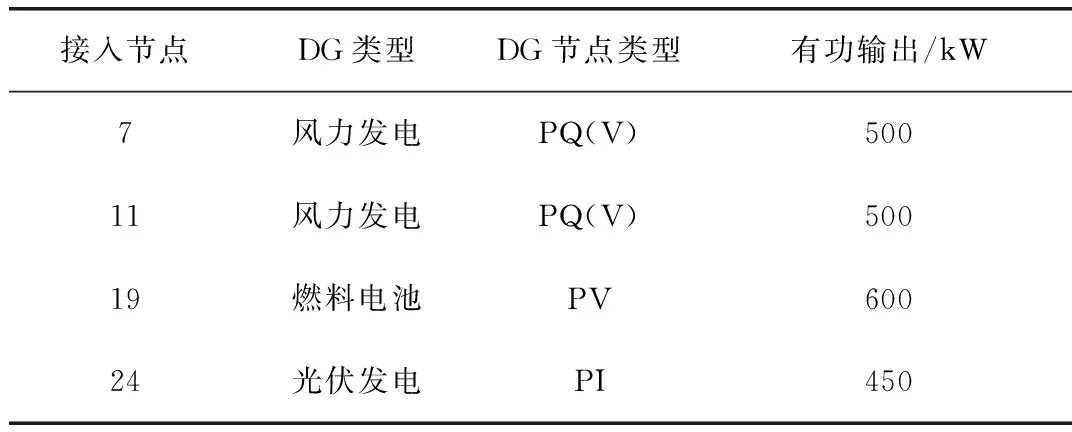
表1 DG接入位置及容量Tab.1 Position and capacity of DG

为更加真实的模拟出实际情况，对DG恒功率模型应使用重构前的DG实际输出功率作为该模型下DG的功率。对重构前的原始网络使用所述DG通用模型进行潮流计算，进而确定DG在重构前的实际输出功率。计算结果如表2所示。

表2 重构前DG功率输出Tab.2 Output power of DG before reconfiguration

由于7、11节点接入的DG为风力发电，需要从电网吸收无功功率，故其所产生的无功为负数。用表2中的数据作为DG恒功率模型下DG的功率。使用AFWA对以上两种DG模型进行重构，并使用PSASP对重构后的配电系统进行潮流计算。

采用不同的DG模型进行网络重构的最优方案有所不同，在相同的方案下，使用不同的DG模型进行潮流计算的网损也不同。如表3所示，使用本文所述DG模型进行网络重构时，最优重构方案为{B33, B14, B18,

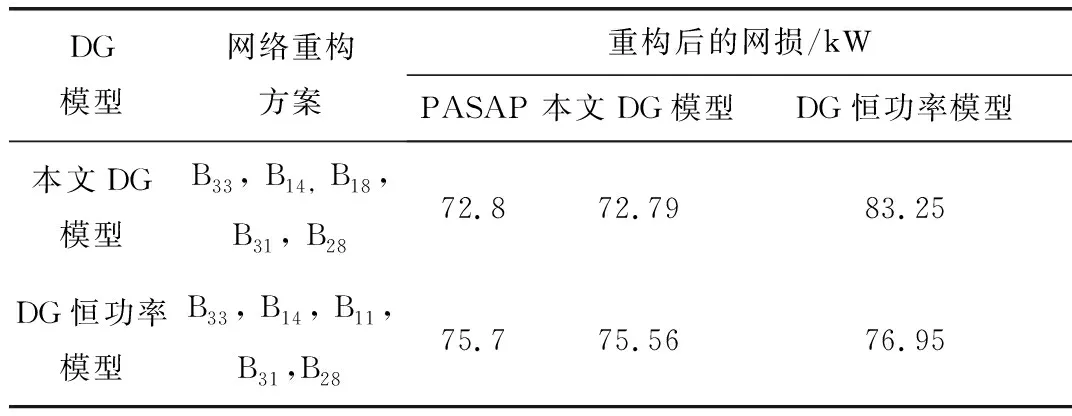
表3 重构结果比较Tab.3 Comparison of reconfiguration results

B31, B28}，在该方案下，使用PSASP计算的系统网损为72.8 kW，使用本文所述DG模型进行潮流计算的网损为72.79 kW，使用DG恒功率模型进行潮流计算的网损为83.25 kW；使用DG恒功率模型进行网络重构时，最优重构方案为{B33, B14, B11,B31,B28}，在该方案下，使用PSASP中计算的系统网损为75.7 kW，使用所述DG模型进行潮流计算的网损为75.56 kW，使用DG恒功率模型进行潮流计算的网损为76.95 kW。由上述数据可以得出，使用所述DG模型计算的网损与PSASP更加接近。

产生上述情况的主要原因是DG的实际无功输出主要与DG的节点电压有关，而配电网的网络结构改变会使节点电压发生变化。在所述DG模型中，考虑了电压变化对DG出力的影响，而DG恒功率模型中未考虑DG出力的改变，由于在重构过程中DG出力与初始网络相比可能会发生较大的变化，因此两种DG模型的重构后最优方案会有所不同。在相同的方案中，所述DG模型能够根据DG节点电压重新确定DG的无功输出，DG恒功率模型仍使用重构前的功率输出进行潮流计算，因此使用所述DG模型可以更加接近配电网实际的网络损耗。

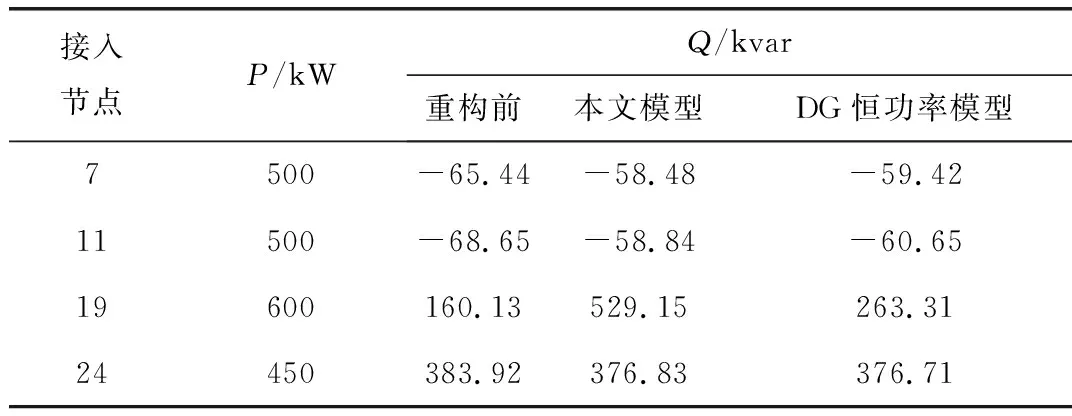
表4 重构后DG功率输出Tab.4 Output power of DG after reconfiguration

在不同的重构方案中，DG的节点电压也有所不同，导致DG的无功出力发生改变。表4记录了重构前以及两种重构方案后的DG实际输出。

由表4可以看出DG在重构过程中，由于系统结构的改变，DG输出的无功功率也发生了改变。所述DG模型中无功发生改变较大，其主要原因是，该模型下计算的网络损耗是通过DG参与迭代的潮流计算方法。该模型可以通过改变配网结构影响各节点电压，进而改变DG无功输出，从而寻找到合适网络结构，使DG合理化输出，最大限度地降低系统网损。DG恒功率模型中，无功发生的变化较小，其主要原因是，在该方案下计算的网络损耗是将DG输出作为固定值，不参与潮流计算的迭代，因此，该方案下重构后的DG输出与重构前的输出相差不大。这也是两种DG模型产生不同方案的主要原因。

图4记录了电压分布情况。为表述方便，这里规定方案一为使用本文所述DG模型的重构方案{ B33, B14, B18, B31, B28}，方案二为使用DG恒功率模型的重构方案{ B33, B14, B11, B31, B28}。分别对两种方案使用不同的模型计算节点电压分布。

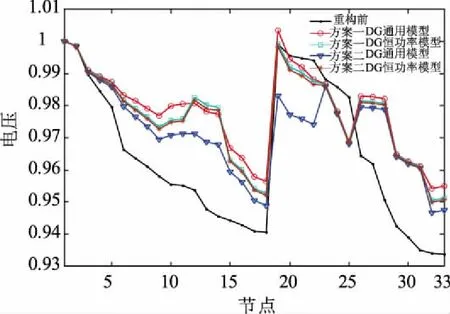
图4 电压分布图Fig.4 Distribution diagram of voltage

如图4所示，两种重构方案在不同的潮流计算中电压均有所改善。在方案一中，使用所述DG通用模型的潮流计算，电压改善最为明显。其中19节点的电压为1.003 3 p.u.，其主要原因是由于直接和等效成PV节点的燃料电池相连，DG可以注入较大的无功功率，使该节点电压大于 1 p.u.。但在该方案中，使用DG恒功率模型进行潮流计算，电压与所述DG通用模型的潮流计算相差较大，主要原因是在该模型的潮流计算中DG仍采用重构前的DG输出，无法给节点提供充足的无功，进而使得电压较低。在方案二中，采用两种潮流计算后的电压相差不大，主要原因是使用DG恒功率模型的重构方案中，将DG作为固定的功率源输出，重构后的网络在该固定的功率下可以较好地降低网损并改善电压分布，且从表4中可以反映出在该方案下的实际DG无功输出与重构前的相差不大。

为进一步验证所述DG通用模型在潮流计算中的真实值，将方案一中使用PSASP计算的电压与所述DG通用模型计算的节点电压相对比，如图5所示。

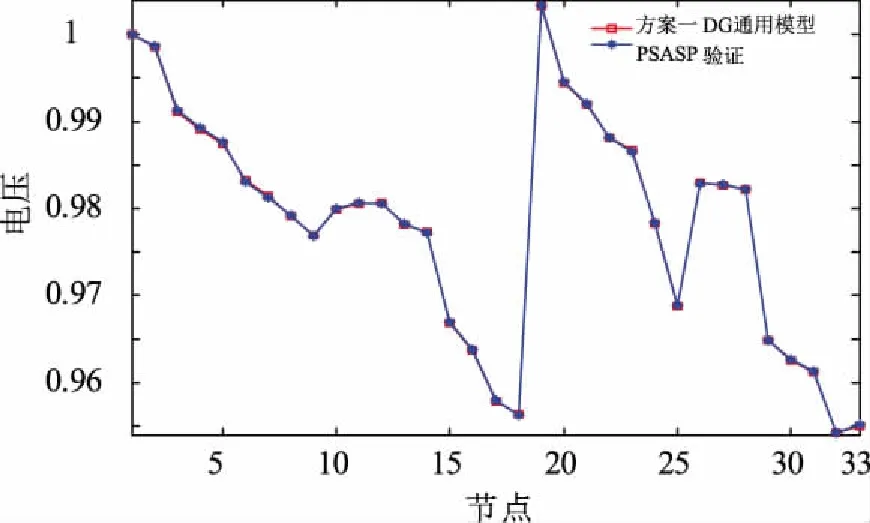
图5 电压分布图Fig.5 Distribution of voltage

由图5可以看出，所述DG模型与PSASP中计算的电压分布曲线基本重合，验证了所述DG模型在潮流计算中可以更加真实的反映出配电网的实际潮流。

4.2 情况二

为进一步寻找两种DG模型产生最终重构方案不同的因素，保持DG类型以及接入点位置不变，改变DG出力大小。对重构前的原始网络使用所述DG通用模型进行潮流计算，进而确定DG在重构前的实际输出功率，如表5所示。

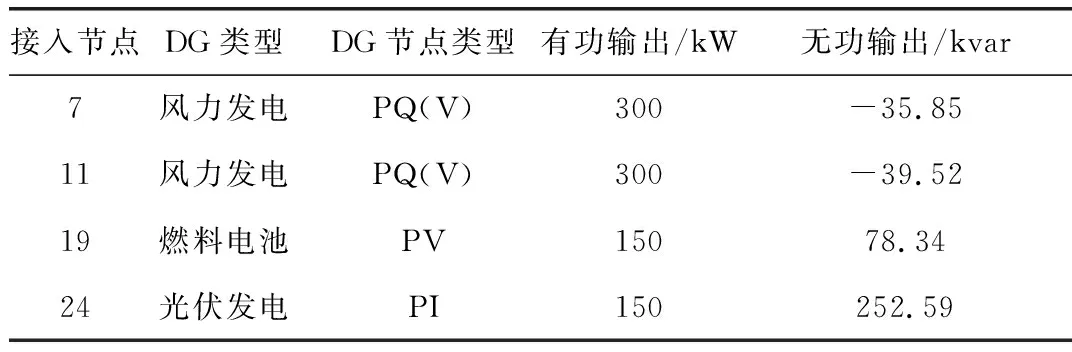
表5 DG参数Tab.5 Parameters of DG

使用AFWA对以上两种模型进行网络重构。

表6 重构比较Tab.6 Comparison of reconstruction

由表6可以看出，DG出力较小时，使用两种模型最终生成的方案相同，且系统网损相差较小。其主要原因是DG出力较小，且在重构前DG已经接近其出力的最大值，在重构过程中对重构的方案影响不大。

由表7可以看出DG在重构过程中，由于系统结构的改变，DG输出的无功功率也发生了改变。与19节点相连的燃料电池无功输出由原来的78.34 kvar升至132.29 kvar，主要原因是初始网络中燃料电池简化的PV节点无功没有越限，重构后该节点无功越限，转化为PQ节点，输出最大无功为132.29 kvar。与7、11节点相连的风力发电无功输出改变较小，该DG与电网并网时加入了无功补偿设备，保证了功率因数。与24节点相连的光伏发电无功输出略微降低，主要原因是在重构前该DG已达到最大无功输出，由于配电网络结构改变，使节点电压发生变化，导致最大无功输出改变。

表7 重构后DG功率输出Tab.7 Power output of DG after reconstruction

在该方案下的两种模型潮流计算后的电压分布如图6所示。

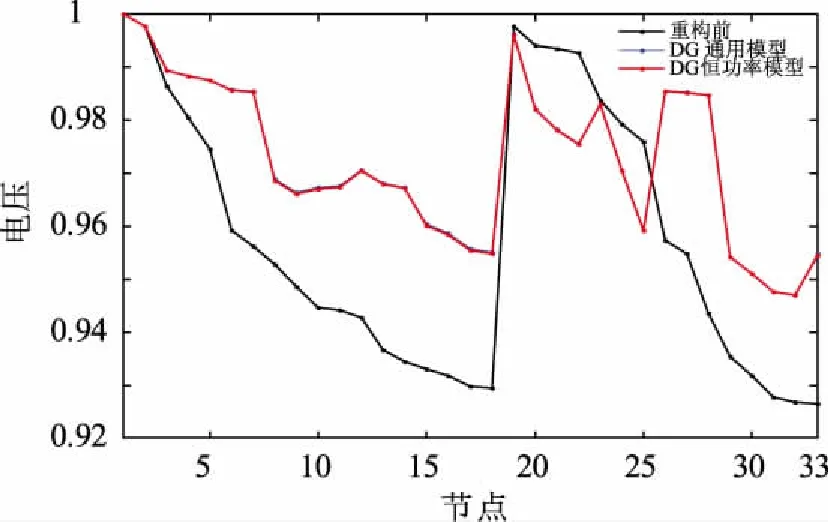
图6 电压分布图Fig.6 Distribution of voltage

如图6所示，两种模型重构后的节点电压基本相同。主要原因是重构后的配电网断开开关相同，总体的无功改变较少相对于整个配电系统来说影响不大。

综上所述，使用DG恒功率模型的配电网重构虽然可以有效改善系统的网损，但是在DG的额定功率较大时，该模型下重构的方案没有考虑电网电压对DG出力的影响，没有寻找到网损最低的重构方案。所述DG通用模型不仅可以准确的计算出配电网的实际潮流，而且充分考虑了电网电压对DG出力的影响和DG无功最大值的约束条件，在DG额定功率较大时可以比较好的利用DG出力降低网损，重构后的系统网损更接近真实值。

5 结束语

提出一种考虑不同DG属性的通用模型，该模型中考虑了配电网络结构和节点电压改变对DG出力的影响。采用AFWA对配电网进行重构，将所提DG通用模型与DG恒功率模型相对比，使用所述DG通用模型的配网重构能够准确的寻找到最优网络重构方案，有效降低网络损耗并改善电压分布。在DG额定功率较大时，两种模型在配网重构中形成的重构方案不同，而对同一个重构方案所述DG通用模型可以更加准确的计算出系统网络损耗和电压分布。