自适应逐次逼近的粗时段导航算法

王民康，孟海螺，秦红磊

(1.北京航空航天大学 电子信息工程学院，北京 100191；2.中国兵器工业集团第二○五研究所 总体五部，西安 710065)

0 引言

全球卫星导航系统(global navigation satellite system，GNSS)由于其全球性、全天候、全时段、实时、高精度的特性得到了广泛的应用，而随着时代的发展，GNSS不断在各个领域衍生出新的应用。尤其是1996年美国通讯委员会颁布了“E911”的行政性命令，要求任何时间、地点都能通过手机追踪到用户，使得基于位置的服务(location based service，LBS)逐渐受到了重视并且需求越来越大。LBS主要面向的是如手机和个人数字助理等终端，在这些应用中，首次定位时间(time to first fix，TTFF)、成本、功耗成为了接收机的严格指标。现有的LBS技术中，主要有到达时间(time of arrival，TOA)、入射角(arrival of angle，AOA)、辅助GNSS(assisted-GNSS，A-GNSS)以及用于室内定位的无线保真(wireless fidelity，WiFi)等；这其中，A-GNSS既保留了传统GNSS技术的优良特性，又有快速定位和高灵敏的优势，得到了最为广泛的应用[1]。

A-GNSS由辅助服务器通过通信网络提供给接收机辅助信息，包括时间、位置、卫星星历和历书等数据，以此来辅助解算相关信息，降低首次定位时间。传统接收机中，卫星的发射时间是计算全伪距和卫星位置的前提条件；而A-GNSS中卫星发射时间可以由精时间辅助或者解调导航电文得到。当只能得到一个粗略的辅助时间，并且无法解调得到卫星信号发射时间时，卫星发射信号时刻的具体位置将不能确定，也就是产生了粗时段导航问题。为了解决粗时段导航问题，文献[2]提出了Range Fit方法，引入Lambda-fraction函数来求解卫星发射时刻的毫秒整数部分；但其要求提供一个误差小于150 km的初始用户位置，且没有解决毫秒整数的模糊问题。文献[3]提出一种重构全伪距的方法来解决毫秒整数的模糊问题，通过引入一个新的变量即粗时间误差到导航定位方程中来解决粗时间问题；算法要求提供一个100 km误差以内的初始位置和1 min误差以内的初始时间。文献[4]在此基础上，提出了一种不需要初始位置的粗时段导航算法，先验位置由多普勒定位算出。文献[5-6]的进一步研究使得初始时间的误差放宽到12 h，甚至几天。

但是，相对于常规导航定位解算方程，粗时段导航方程存在着定位精度较差的问题[5]。粗时段导航方程在构建状态矩阵时将伪距速率设为恒定值，而由于卫星加速度和卫星时钟速率变化率的存在，迭代解算时会引入线性化误差。文献[7]的实验结果表明，随着粗时误差的增大，粗时导航解算的定位误差也随之增大。此外，文献[8]证明了由于粗时导航方程中添加了一个额外的状态，使得所有的精度衰减因子(dilution of precision，DOP)都会大于或等于原始的四状态导航方程对应的值，从而使得最终的定位误差变大。

本文针对粗时段导航解算中存在的定位误差问题，提出一种自适应逐次逼近的粗时段导航算法。该算法通过每次迭代时更新卫星发射时间和位置以及伪距速率来减小线性化误差，并在解出精时间后重新推入四状态导航方程以解决DOP问题。

1 粗时段导航

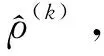
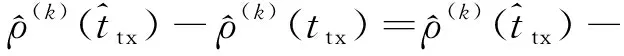
(1)

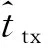
因此，新的伪距残差可以表示为

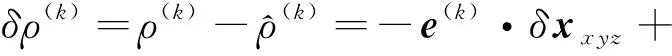
(2)

式中：δxxyz为三维向量，是δx的空间元素[δx，δy，δz]T；ε(k)为测量误差；δb为公共偏差的状态更新量。

那么扩展到N颗可用卫星的情况，可得一个新的矩阵方程组

δρ=Hδx+ε

(3)

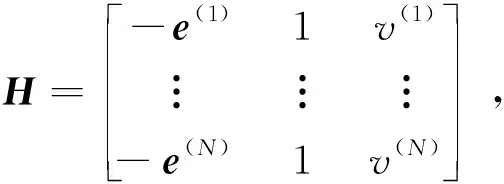
从几何矩阵H中可以看出，至少需要独立的5行变量才能求解出δx；因此粗时段导航需要至少5颗不同的可用卫星。

然而，由于多数情况下完整的伪距测量值ρ(k)没有得到，仅能由捕获或跟踪得到扩频码码相位值，测量伪距将是一个亚毫秒值。由于未知的常见偏差的存在，使得粗时段导航还存在着毫秒整数模糊的问题。文献[3]给出一种重构全伪距的方法来解决整毫秒模糊问题，流程如下：

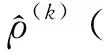
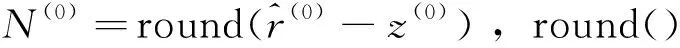
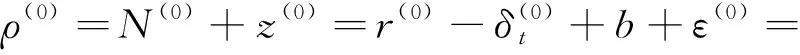
(4)

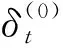
3)计算按照仰角排序列表中的下一颗卫星k的整毫秒伪距值N(k)。其重构的全伪距和其期望伪距的关系为

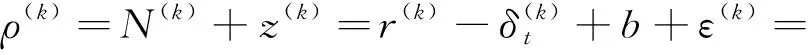
(5)

式(5)和式(4)相减可得：

(6)

式(6)消除了公共偏差b。当-d(k)+ε(k)-d(0)+ε(0)的绝对值小于0.5个光毫秒时，k号卫星的整毫秒伪距可以估计为

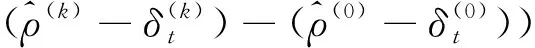
(7)

从而得到k号卫星的全伪距ρ(k)=N(k)+z(k)。

4)更新参考卫星为上一个计算完的卫星，然后到步骤3)，计算下一颗卫星的全伪距。

要使得重构全伪距算法有效，从式(7)中可知，先验位置和时间引起的误差需要在150 km以内。通常在A-GNSS系统中，先验的位置和时间信息可由通信网络提供，位置可通过Cell-ID等技术得到，一般精度可达3 km；而GSM网络可提供1～2 s的时间精度，可满足上述约束条件。一般来讲，100 km以内的先验位置误差和1 min以内的先验时间误差可以使得上述重构全伪距算法一直有效。

2 粗时段导航算法中的定位误差分析

2.1 粗时段导航中的线性化误差

粗时段导航通过添加粗时间这个新的状态来解决粗时间的问题。在第1节中可以看到粗时段导航的4个步骤，当计算得到状态更新向量之后，将会调整先验状态，也就是先验位置、公共偏差和粗时间。几何矩阵H中的接收机与卫星连线单位矢量e(k)会依据先验状态进行更新；而一般来讲，粗时段导航中，卫星的位置在每次迭代中不会更新，依靠几何矩阵H中第5个状态v(k)来补偿卫星位置引起的误差。通常v(k)也不会每次迭代都更新，而是在粗时段导航定位解算过程中保持不变。卫星的运动存在加速度和加加速度，速度并非恒定值，对卫星的速度进行建模，可以表示为

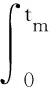
(8)

式中：v(tm)为卫星在时刻tm时的速度；v0为参考时刻的速度；t为时间单位；a(t)为与时间有关的加速度。

表1给出了在不同的粗时误差下五状态粗时段导航的3维定位精度比较，所采用的数据为62 MHz采样的实际GPS L1静态数据，每隔1 s时间获取一次码相位测量数据，来进行粗时段导航定位。

从表1中可知：当粗时误差较小时可以得到较好的定位精度；当粗时误差较大时，定位误差增大，定位结果出现较大偏差。这与文献[7]中结果类似。可见粗时段导航中的线性化误差不能忽略。

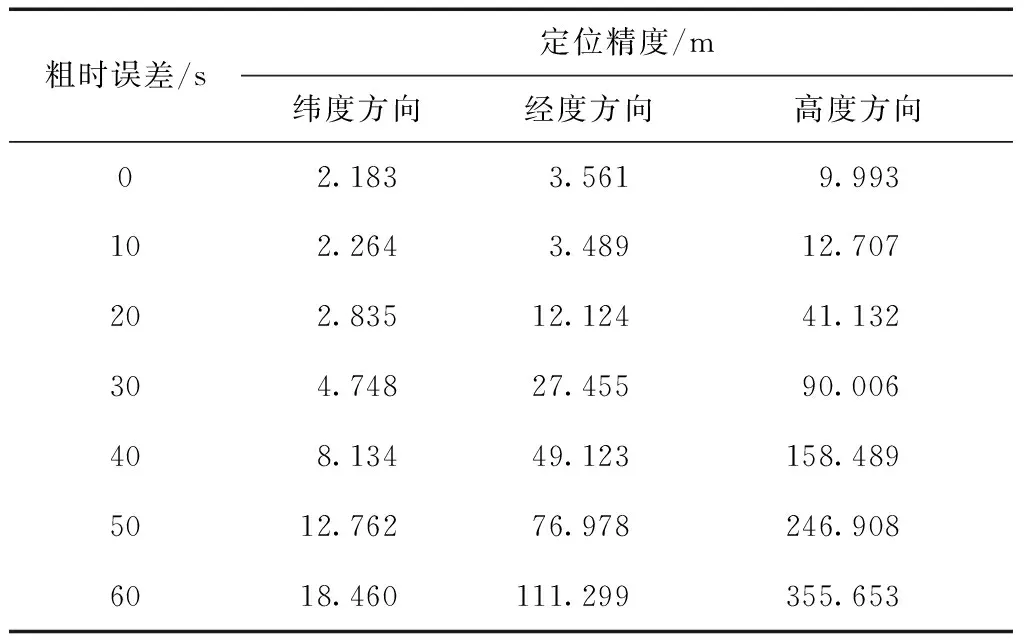
表1 不同粗时误差下粗时段导航算法定位精度

2.2 粗时间精度衰减因子

粗时段导航由于在几何矩阵H中多加了1个状态，进而影响了精度衰减因子，使得当卫星数较少时粗时段导航几何精度衰减因子(geometric dilution of precision，GDOP)比四状态的GDOP大；而卫星数较多时二者差距较小。由式(3)可以得到状态更新量估计值

(9)

可见，定位误差与几何矩阵相关。而由于几何矩阵增加了1个状态，会使得所有的DOP值大于或等于原来的值。定义GDOP[9]为

(10)

式中：G=(HTH)-1为权系数阵；trace()为求矩阵迹的运算。

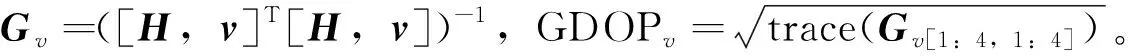
(11)

式中：M=HTH；P=HTv；N=vTv。

进一步展开可得

(M-PN-1PT)-1=M-1+
M-1P(N-PTM-1P)-1PTM-1

(12)

由于式(12)右边第二部分为半正定矩阵，其迹大于等于0；因此有

(13)

图1 四状态导航和五状态粗时段导航可见卫星数目和HDOP值比较

图1展示了常规四状态导航和五状态粗时段导航各自的水平精度衰减因子(horizontal dilution of precision，HDOP)的对比，同时给出了可见卫星数量的变化趋势。从图中可以看到五状态促使到导航的HDOP总是大于或等于四状态导航的HDOP，满足理论分析。可用卫星多的情况下二者HDOP接近，可用卫星少时二者差距较大；从而导致五状态粗时段导航定位误差比传统四状态导航的定位误差大：因此在解决粗时段导航问题时不能忽略DOP问题。

3 自适应逐次逼近的粗时段导航算法

为了解决粗时段导航中的线性化误差和DOP问题，以尽可能地提高其定位精度，本文提出一种自适应逐次逼近的粗时段导航算法。在每次得到状态更新解之后，重新计算卫星信号发射时间，并重新计算卫星位置和速度，更新几何矩阵H，逐次逼近最终解，解决线性化误差。在五状态解算完成之后，检验卫星数和DOP，如果不满足要求，自适应推入四状态导航方程重新解算，解决DOP问题。图2给出了该算法的实现流程。

算法具体步骤如下：

1)由辅助网络得到先验位置和一个粗略的时间作为初始解，设初始公共偏差为0。

2)利用当前的时间解和重构的全伪距计算各卫星信号发射时间，并由辅助星历计算各卫星的位置、速度、卫星时钟偏差速率和伪距误差校正量。再利用当前用户位置解和卫星位置计算预期伪距，计算误差校正后的测量全伪距。

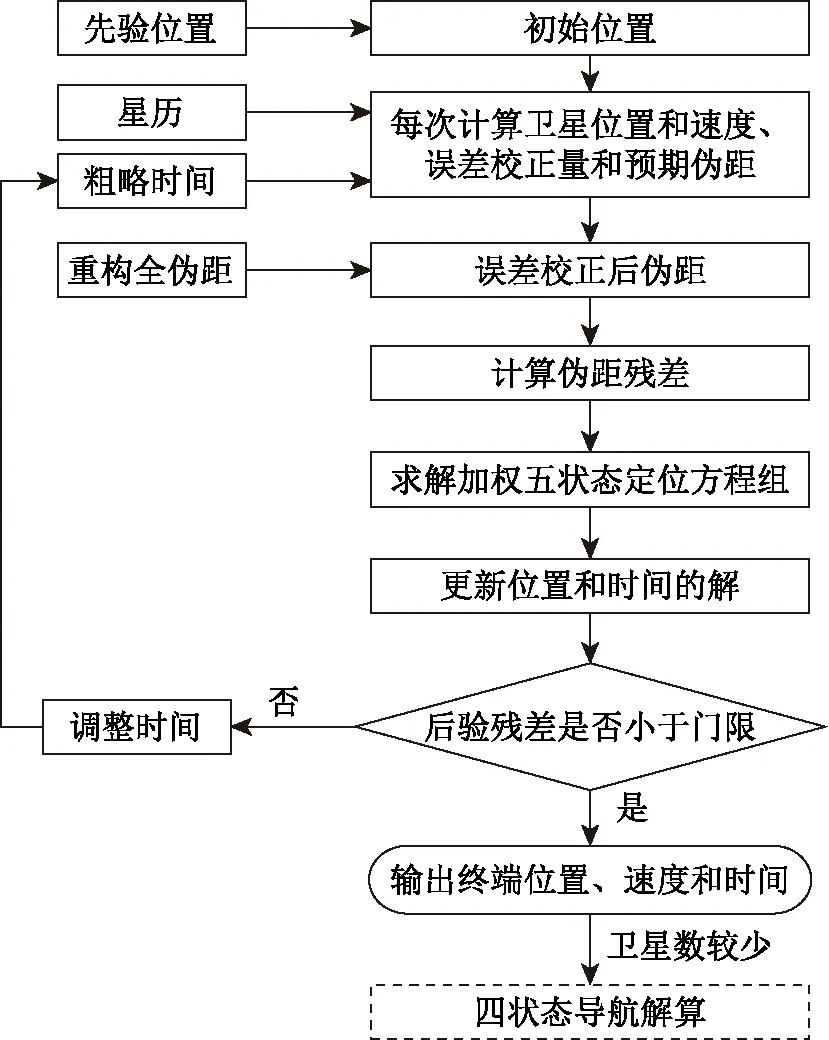
图2 自适应逐次逼近的粗时段导航算法流程

3)对式(3)引入加权系数，使得其误差的方差进一步减小，可得

WH·δx=Wδρ

(14)

δx=(HTCH)-1H-1C·δρ

(15)

式中：C=WTW；H为改进的五状态几何矩阵。五状态几何矩阵H表示为

(16)

也就是说，在每次最小二乘运算迭代时会根据当前计算得到的用户位置解和时间解更新五状态几何矩阵H各参数。同理，每次迭代时的伪距残差为

(17)

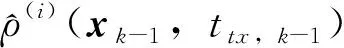
4)计算后验残差，如果足够小，则输出当前解最后用户的位置和时间解结果；否则，根据当前解重新计算各卫星信号发射时间，返回步骤2)。

5)由于五状态导航的DOP值始终大于或等于四状态导航；当由上述加权五状态粗时段导航方程求得用户位置和时间解之后，将其解结果作为四状态的初始状态，进行四状态导航方程解算。文献[10]表明，当卫星发射时间精确到10 ms以内时可以保证四状态导航方程有效；从而可以通过将五状态粗时段导航方程再次推入到四状态导航方程中进行解算，来降低粗时段导航中的各DOP值，进而提高定位精度。

4 实验与结果分析

为了验证自适应逐次逼近粗时段导航算法的效果，本文进行了一系列实验来进行验证。采用自研多模多频点GNSS信号采集器获取实际环境中的GPS L1的静态数据进行算法验证实验。

信号的采样率为62 MHz，中频为4.17 MHz。算法为每隔1 s获取一次码相位测量量，码相位由高灵敏捕获模块得到，并经过码相位精化方法提高捕获所得码相位的精度。先验位置给定为距离信号采集地点约430 m的位置，信号采集处的精确位置事先由高精度载波相位差分接收机测得，分别取粗时误差为0、10、20、30、40、50、60 s来验证本文算法在不同粗时误差下的定位性能。

图3给出了当粗时误差为60 s时，自适应逐次逼近粗时段导航算法在纬度、经度和高度3个方向上的定位结果，并给出了与真值的对比。

图4给出了粗时误差为60 s时自适应逐次逼近粗时段导航算法和无粗时误差时四状态导航定位结果的均方根误差(root mean square error，RMSE)的对比。此处四状态导航解算中所用码相位结果与粗时段导航中所用码相位相同。

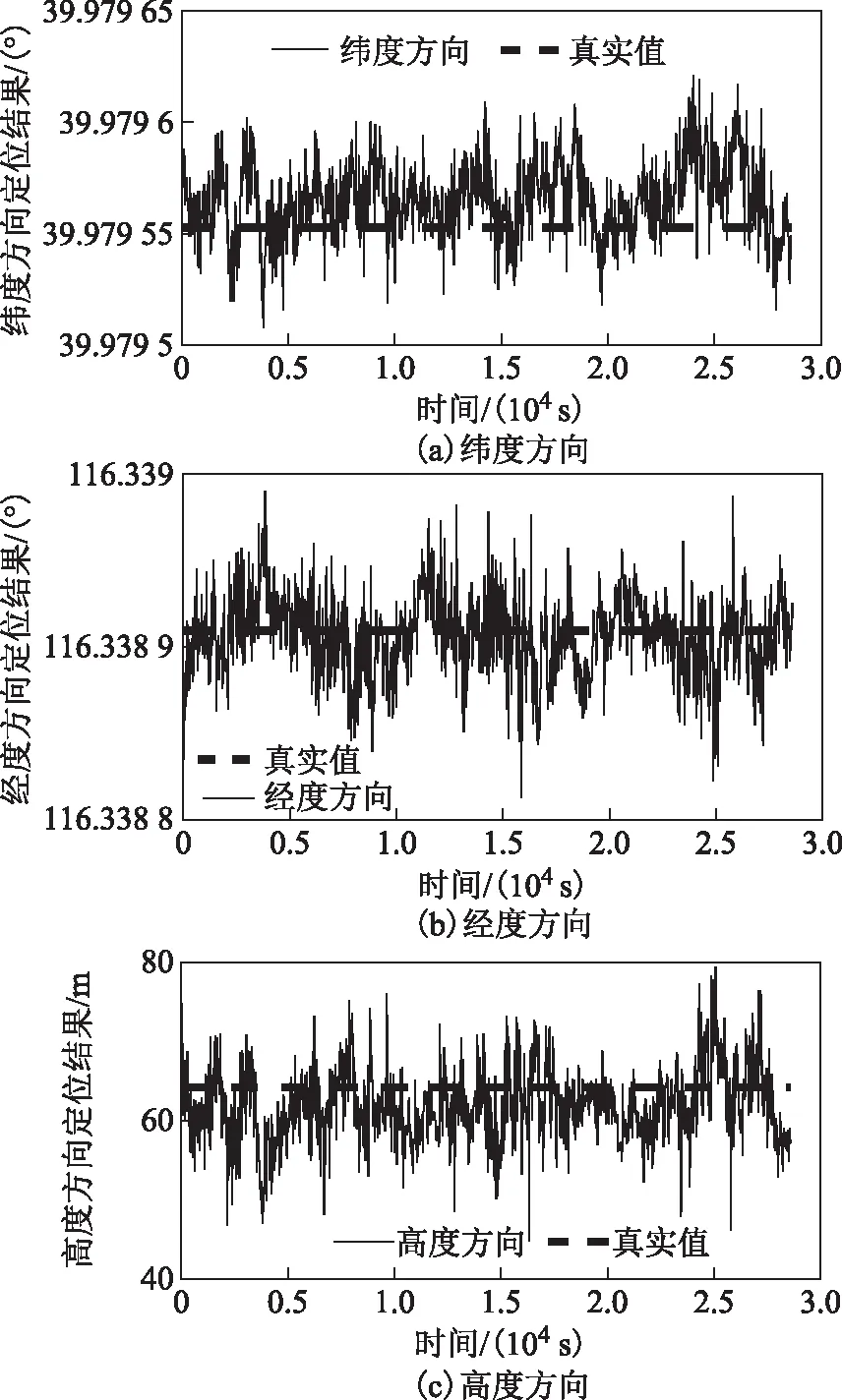
图3 粗时误差为60 s时改进粗时段导航算法定位结果

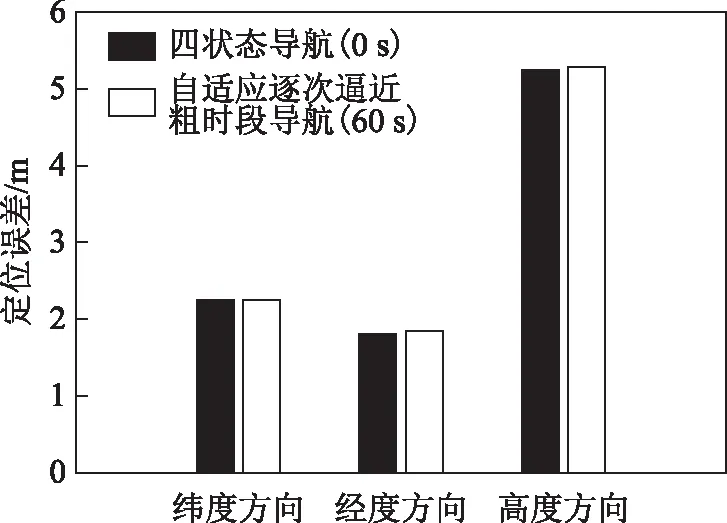
图4 粗时误差60 s时自适应逐次逼近粗时段导航与无粗时误差四状态导航定位精度对比

从图3和图4可以看出：自适应逐次逼近粗时段导航在粗时误差大到60 s时仍能获得较高精度的定位结果；经度和纬度方向上定位结果的RMSE均大约为2.2 m左右，高度方向上定位结果的RMSE大约为5.2 m左右，并且该定位结果与无粗时误差时常规四状态导航定位结果基本相同。可见，自适应逐次逼近粗时段导航算法在有较大粗时误差时仍能获得与常规四状态导航定位接近的较高的定位精度。

表2给出了在不同粗时误差下，自适应逐次逼近粗时段导航算法定位结果的RMSE之间的对比。

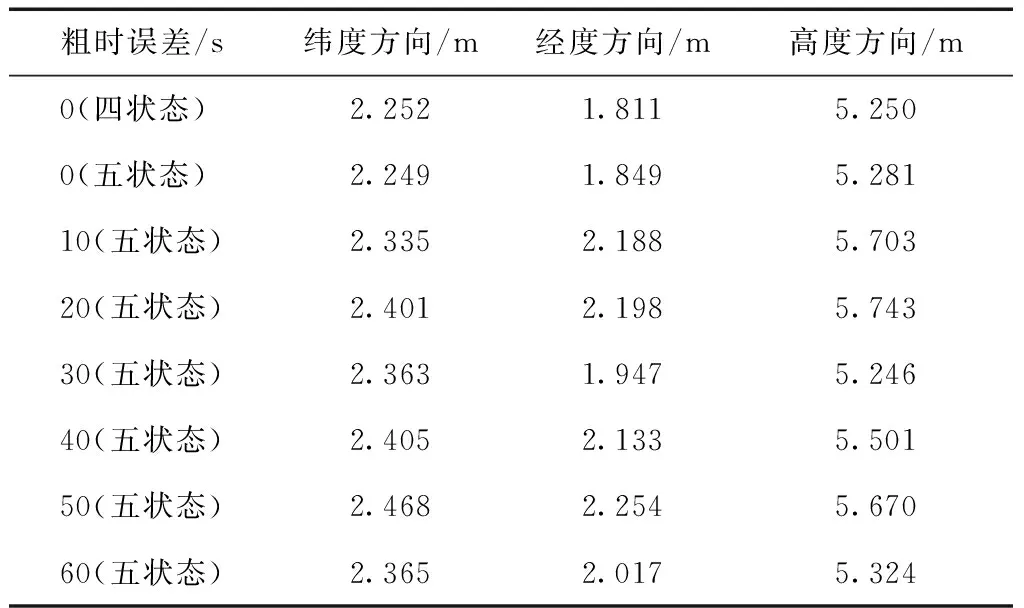
表2 不同粗时误差下自适应逐次逼近粗时段导航算法定位结果的RMSE

从表2可以看到：当粗时误差从0～60 s变化时，自适应粗时段导航算法都能够获得较高的定位精度；纬度和经度定位结果的RMSE都在2.5 m以内，高度的RMSE在6 m以内，这与四状态导航方程所得到的定位结果接近。这表明本文所提出的算法克服了在较大粗时误差下粗时段导航存在的线性化误差以及五状态导航定位比四状态导航定位DOP大的问题，获得了较高的定位精度，保证了粗时段导航在大粗时误差或者可用卫星数较少时仍能获得与常规定位解算接近的较好的定位结果。

5 结束语

本文针对GNSS导航定位中粗时段导航存在的大粗时误差下线性化误差问题和DOP问题，提出了一种自适应逐次逼近的粗时段导航算法。在粗时段导航算每次迭代运算时，同时更新卫星状态和几何矩阵，并在解算完成后自适应推入四状态导航算法重新解算，保证了在较大粗时误差下或者卫星数较少时粗时段导航仍可获得较高的定位精度。通过采用实际GPS数据的相关实验，验证了该算法的有效性和可靠性。实验的结果表明：自适应逐次逼近的粗时段导航算法在0 s的粗时误差下能够获得与常规四状态导航算法近似的定位精度；纬度和经度定位结果的RMSE在2.2和1.8 m左右，高度定位结果的RMSE在5.2 m左右，算法连续测试了20 min左右的数据，具有连续可用性；随着粗时误差的增大，定位精度基本保持不变，在较大粗时误差下仍能获得与粗时误差为0 s时接近的定位结果。

本文提出的自适应逐次逼近粗时段导航算法使得在存在粗时间问题时GNSS导航定位方法仍然可行，并且在恶劣环境下，如大粗时误差或可用卫星少时，仍能得到较好的效果，扩展了粗时段导航的应用场景，增大了GNSS导航定位的可用性。