圆幂定理在椭圆上的推广及其若干推论

江西省赣州中学 (341000) 谢玉兰

椭圆是圆通过一个特殊的仿射变换得到的一种圆锥曲线，它们之间有着一个特殊的仿射关系，利用这一关系可以把圆的一些性质定理推广到椭圆上，也可以直接用这一关系来得出椭圆的若干推论.把握好椭圆与圆的这一仿射关系，可以帮助我们更多更深入地了解椭圆的性质.

1.圆幂定理

圆幂定理过平面上一个定点M,任作一直线与半径为r的定圆交于A,B两点，则MA×MB为定值k(这里MA,MB表示有向线段的数量),并且k=OM2-r2.定值k叫做点M关于圆O的幂,简称圆幂.

2.圆幂定理在椭圆上的推广

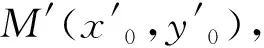
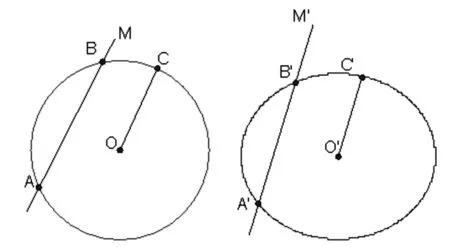
图1 图2

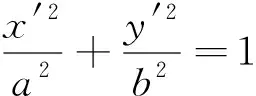
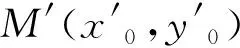
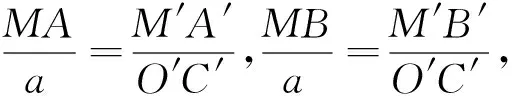
3.圆幂定理在椭圆上的若干推论

与圆幂定理相类似，由椭圆幂定理我们又可以推出椭圆的相交弦定理,切割线定理和切线长定理.

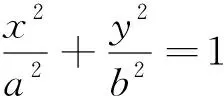
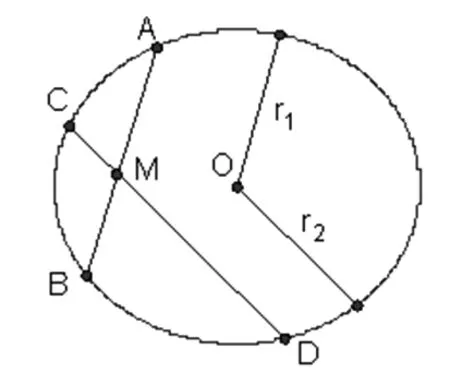
图3

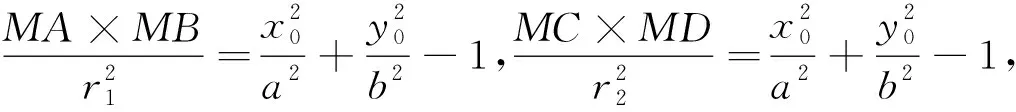
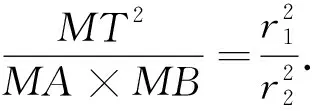
证明:椭圆O的切线MT和割线MAB交于点

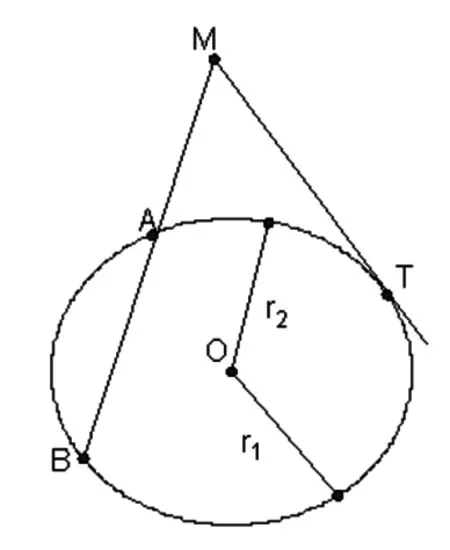
图4

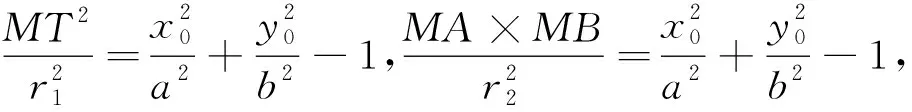
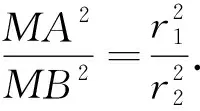
证明:椭圆O的两条切线MA,MB交于点M(x0,

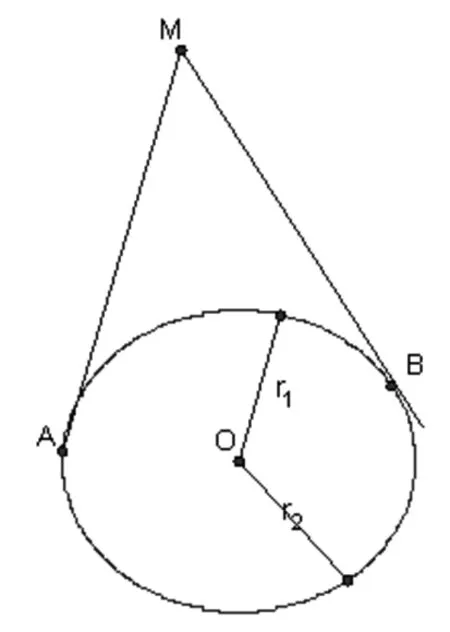
图5

4.结语

本文对圆与椭圆之间的关系应用仿射关系来解释即椭圆是圆经过一特殊的仿射变换后的二次曲线，丰富了传统的对椭圆的理解.同时把圆的圆幂定理推广到椭圆上，给我们解题带来了方便.