旋风除尘器最优化设计及CFD数值验证

郗 元 ，霍 浩 ，代 岩

1 引言

随着我国工业的迅猛发展，工业生产过程中产生的粉尘已成为造成雾霾的主要原因。究其根本必须做好对粉尘源头的控制，这是最直接也是最有效的治理方法[1]。旋风除尘器作为高效率、低能耗的除尘设备，广泛应用于能源及环保行业中。文献[2]设计了一种用于回收烟气余热的套管换热式旋风除尘器，热回收量可以提高（1.33～3.06）倍。文献[3]通过引入喷雾降尘技术提高了旋风除尘器的除尘效率，并结合MATLAB对其进行了不同压力的计算。文献[4]结合神经网络对旋风分离器进行了多目标优化研究。

上述研究均从不同角度提高了旋风除尘器的性能，但很少有学者针对全局结构参数进行整体优化分析。通过建立除尘效率理论计算模型，综合考虑各结构影响参数，并结合MATLAB进行寻优计算，对新结构下旋风除尘器内部流速、压力及除尘效率进行数值模拟分析，验证理论模型，确定最优结构参数的可行性。

2 物理模型

某型号旋风除尘器结构示意图，如图1所示。其主要结构包括旋风除尘器入口高度a、入口宽度b、筒体高度H；出气口直径Dc、插入筒体深度 L；筒体直径 D0、高度 Hc；排灰口直径 Dd。

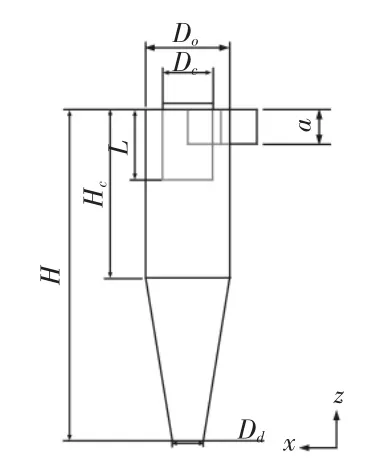
图1 旋风除尘器结构示意图Fig.1 Structure Diagram of Cyclone Dust Collector

3 数学模型构建

选取除尘效率作为旋风除尘器分离性能的优化目标，并结合Leith-Licht设计法[5]，建立数学模型。

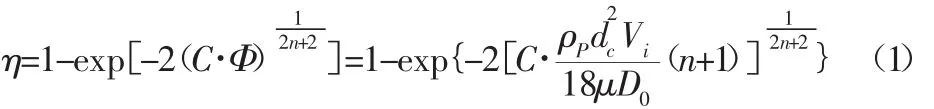
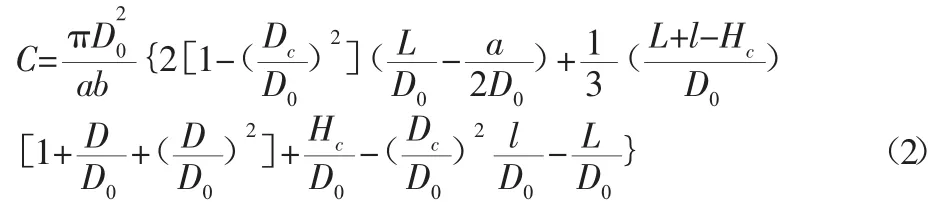
结合井伊谷钢一的普通直入型旋风分离器的压力损失公式[6]：

式中：K—常数，取16；Vi—进风口速度；ρ—气体密度。

将Vi=Q/ab代入式（3），并整理得

结合除尘器设计手册等[7]，旋风除尘器各结构参数应满足如下要求：入口宽度与排气管壁到器壁的距离应该满足以下关系：

旋转涡流延伸到的位置应到达锥筒底部，即满足以下等式（6）关系

令D20/ab=M，则CΦ=CM·Φ/M，对于任何固定值Φ/M，都代表着一定性质的粉尘和运载介质（如空气）的流动情况。当CM取得最大值时，除尘效率ηi取得最大值。故把G=CM作为优化设计得目标函数，通过整理得出目标函数表达式如下：

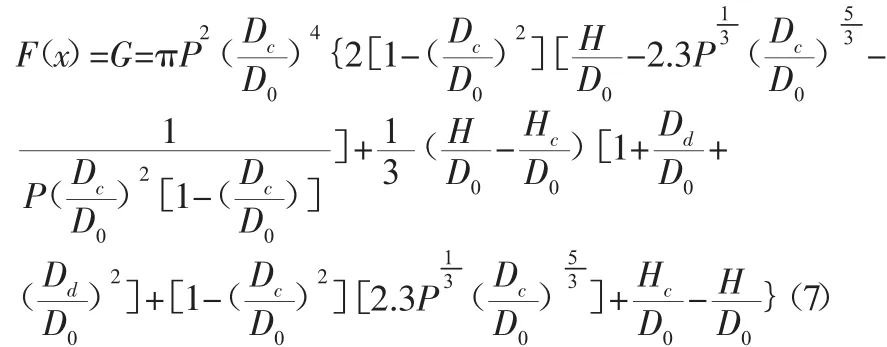
优化设计所需约束条件如下：

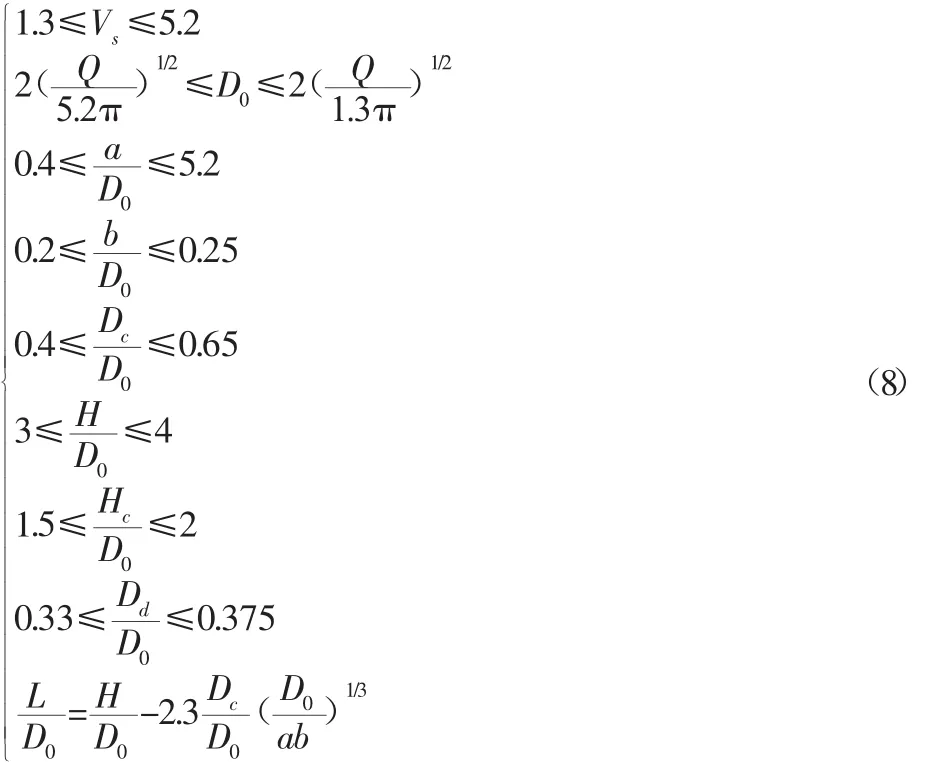
在设计旋风除尘器时，通常处理风量Q和压力损失ΔP为给定量，通过目标函数表达式不难看出，在Q和ΔP给定的情况下，目标函数的大小只与旋风分离器的各结构尺寸有关，故选取优化设计变量X如下：

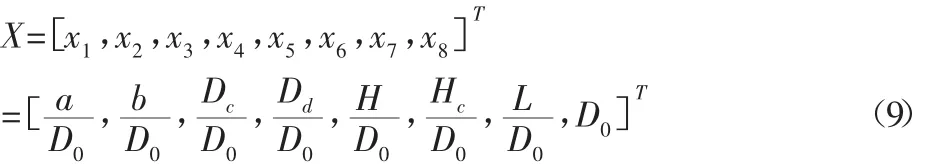
结合MATLAB对该非线性极小值优化问题进行求解，计算结果，如表1所示。

表1 旋风除尘器最优结构计算结果（单位：mm）Tab.1 Optimal Structure Results of Cyclone Dust Collector（unit：mm）

MATLAB优化得到的目标函数最大值为G=4431.0430，而G=C·M=C·D20/ab，从而求得几何特性因数C=354.4834。结合式（1）进行分级除尘效率计算，以粉尘粒密度为1960kg/m3，气体粘度μ为1.72×105Pa·s，室温T为293.15K。选用文献[8]的颗粒粒径分布模型，代入各粒径值和各已知物理量值得到的分级效率列，如表2所示。

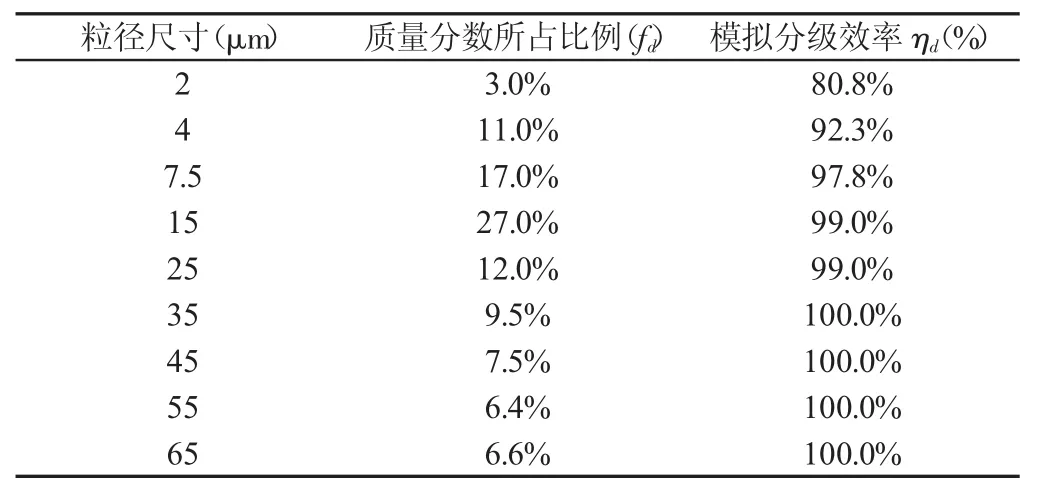
表2 理论计算各粒径分级效率Tab.2 Theoretical Value of Fractional Efficiency for Each Particle Size

旋风除尘器的总除尘效率，如式（10）所示。

式中：fd—不同粒径尺寸的质量分数所占比例；ηd—分级除尘效率因此，求得旋风除尘器总的除尘效率为97.1%。

4 CFD数值模拟验证

根据最优结构参数进行流道模型建立，并对其进行划分网格处理。经过网格无关性分析后，最终确定网格数量为597292，网格模型，如图2所示。

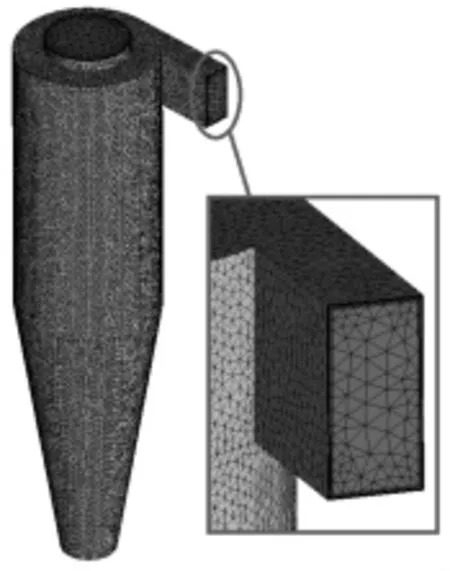
图2 旋风除尘器网格模型Fig.2 Cyclone Dust Collector Mesh Model

边界条件设置：速度进口，速度为12.76m/s，入口速度分布均匀且垂直于入口截面；排气口为压力出口，压力值为标准大气压；壁面为无滑移壁面。考虑旋风除尘器内部的气固两相流动，因颗粒相与气相比所占体积分数较小且低于10%，可采用DPM模型[9-10]。

算法选取：湍流模型采用标准k-ε湍流模型[11]；对流项采用适用于强旋转流具有三阶精度并能减少假扩散的QUICK格式；压力梯度项插补格式的选取最能真实地反映旋风分离器内的强旋流场特性的PRESTO格式；数值计算方法为非交错网格下的SIMPLE算法。

尘土颗粒主要是依靠旋转时受到的离心力来实现分离，因此在旋风分离器的速度场中切向速度占主导地位。旋风除尘器不同Z轴高度位置的切向速度随横坐标x的变化曲线，如图3所示。从图中可以看出，在中心轴两侧随半径的增大，切向速度也随之增大该曲线在中心轴两侧分别存在一个峰值，近似为对称形式。

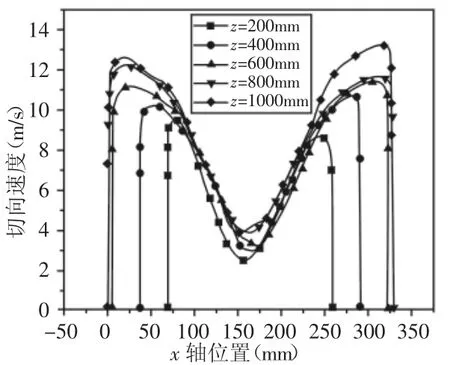
图3 切向速度分布Fig.3 Tangential Velocity

从切向速度的分布曲线可以看出，切向速度呈现为驼峰状，即在轴心处的切向速度最小，在轴心两侧分别有以个峰值，并且该峰值出现在排气管壁位置附近，切向速度具有较好的轴对称性，并且轴心与排气管壁面之间，切向速度的大小沿半径方向随半径增大而增大，而在排气管壁面外部流场区域，随着半径增大而减小，排气管壁面位置处刚好是切向速度峰值。

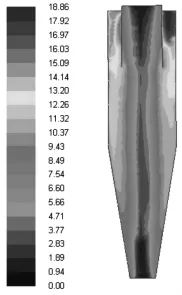
图4 y=0截面速度云图Fig.4 Section Velocity y=0

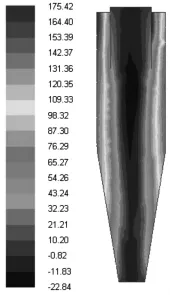
图5 y=0截面静压力云图Fig.5 Section Static Pressure y=0

y=0截面速度云图，如图4所示。从图中可以看出，含尘气流流入后从旋风除尘器的入口开始做加速运动，气流继续加速流动进入旋风除尘器的圆柱形筒，在转弯时速度达到峰值。随后气流沿筒壁作切向速度逐渐减小的圆周运动。排气管中间区域存在明显的低速区域，由于此处速度较低，流场中夹带的粉尘颗粒在这个停留区域容易出现沉积现象。另外，从该截面可以看出，由于排风管底部具有较大的切向速度，这便解释了升气管底端为什么容易发生短路流，从而影响了分离性能[5]。旋风除尘器y=0截面的静压云图，如图5所示。从图中压力分布可以看出静压沿径向的分布比较均匀，并且在轴两侧比较对称，静压的大小沿着半径方向由内到外，压力逐渐增大，并且压力随半径变化的变化率较大。中心轴线附近静压值相对入口处的静压值要小得多，并且中心轴区域静压力值为负，负压区很好的解释了旋风除尘器的中心处于真空状态。沿着轴向来看可以发现，由于在强旋流场中，静压同样受切向速度的影响较大，所以轴向上静压值基本没有变化。另外两个速度分量对静压值的影响相对较小。旋风分离器中心轴线处的静压值在整个流场中相对是最低的，整个中心低压区一直延伸至排尘口端，这便是旋风除尘器锥体底部容易发生滞流或返流问题的原因，如果灰斗底部密封不严，由于中心轴处于负压区很容易倒吸外界气流，这就直接导致了旋风除尘器的分离性能变差。

注入颗粒计算除尘效率时，颗粒射流源类型选用面射流源，面射流源的颗粒初始位置设定在速度进口端面上，并使入射点的位置在进口端面上均匀分布。采用单颗粒相喷射注入法，即每次注入一定直径的单种颗粒。喷射点源为160个，每个点源产生10个颗粒，对总计1600个粒子进行追踪。设置入口喷射速度为12.76m/s，分9次注入流场中颗粒分别检测上排气口逃逸粒子数，从而计算出各分级效率。各粒径分级效率数值模拟结果，如表3所示。

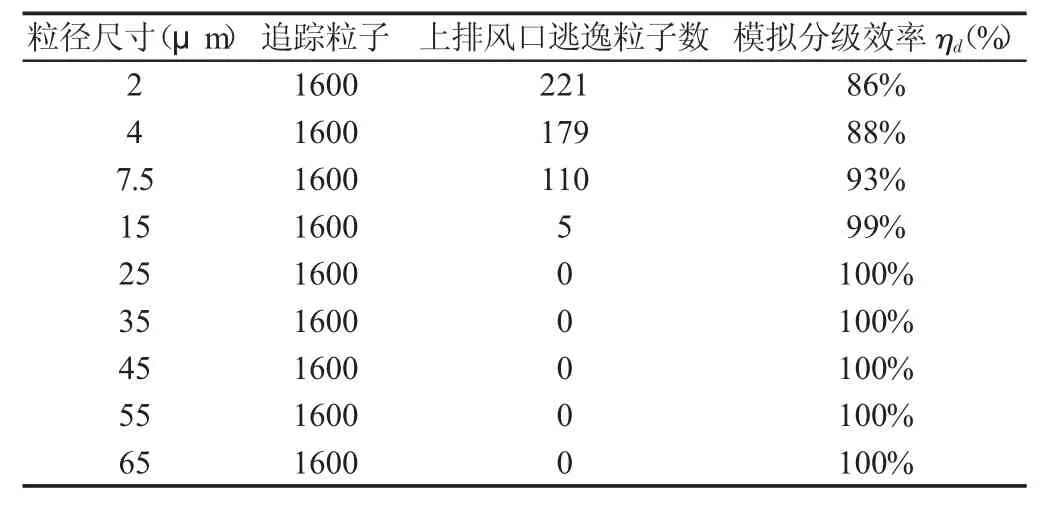
表3 各粒径分级效率数值模拟结果Tab.3 Numerical Simulation Results of Particle Size Fractional Efficiency

根据式（10）可以求得数值模拟计算的总除尘效率的η=98.1%，与理论计算结果97.1%相比，相对误差为：

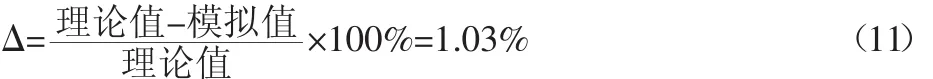
相对误差为1.03%，满足误差允许范围[12-13]，说明数值模拟计算结果与理论计算结果吻合较好，表明设计的优化设计方案是可行的。

5 结论

（1）结合各结构参数对旋风除尘器进行除尘效率数学模型建立，当筒体直径为328.0mm、总高度为1287.5mm、排气管直径为195.1mm、插入深度为246.2mm、入口高度为131.3mm、宽度为65.6mm、筒体高度为656.5mm时，总除尘效率最高，最大值为97.1%。

（2）计算旋风除尘器除尘效率时，不仅可以采用经验公式选型设计，还可以借助CFD技术进行科学验算，缩短设计周期，降低试制成本。