有魔性的单位“1”——《分数除法》解决问题教学设计与解读

陆 雅

【教学内容】

人教版六年级上册第三单元《分数除法》解决问题例7。

【教学设计】

一、创设情境，质疑释疑

1.课件出示信息：一段公路长30千米，工程队修10天完成。

师：读到了什么？想到了什么？

师：为了便于表述，我们把这三个量称为——工作总量，工作效率，工作时间。（板书后，简要讲解三者意义及关系）

【解读：本课是单元最后一个例题，因此问题情境简洁，快速入题。通过简要复习，回顾工作总量、工作效率、工作时间的关系。同时明白工作效率既可以指具体的量“每天修3千米”，也可以是抽象的量“每天修总长度的”。】

2.出示主题图：两个修路队修一条路。工程一队单独修10天完成，工程二队单独修15天完成。两队合修多少天完成？

（1）提出问题，尝试解决。

师：猜猜两队合修需多少天？

生：工程一队单独修10天完成，二队来帮忙肯定比10天少。

师：你觉得解决这个问题，信息够吗？先思考，再用手势表示。

生：信息不够，不知道这条路有多长。

师：你是一位善于思考的学生。这样吧，如果觉得信息不够，那么老师提供了这些数据，你可以选择一个计算。如果觉得信息够了，那就按你自己的想法解决。

出示：一段公路长30千米、长60千米、长120千米、长240千米。

（学生尝试计算，反馈交流）

生：用 30 千米。30÷（30÷10+30÷15）=30÷（3+2）=30÷5=6（天）。

（师生理解算式每一步表示的意义）

生：用 60 千米。60÷（60÷10+60÷15）=60÷（6+4）=60÷10=6（天）

（2）质疑。

生：不用算也知道是6天。

师：不用算也知道，你相信吗？

生：不相信。

师：不相信怎么办？

生：再算，验证。

师生一起计算：120÷（120÷10+120÷15）=120÷（12+8）=120÷20=6（天），240÷（240÷10+240÷15）=240÷（24+16）=240÷40=6（天）

师：现在相信了吗？

生：相信了。

【解读：由前测可知，近40%的学生能利用单位“1”解决问题，但是只有不到10%的学生理解其中的道理，教师让学生先想想信息够不够，再用手势表示，目的在于促使每位学生都能真正思考，展现真实的想法，而不受他人的影响。教师提供四个数据，供学生选择计算，使“走得快”和“走得慢”的学生都有路可走。果然反馈交流时有学生迫不及待地提出：“不用算也知道。”但是教师把关注点再次转向“走得慢的学生”，问：“你相信吗？”“不相信怎么办？”经过再次计算，学生心里自然种下一粒猜想的种子：“是不是与总长度无关？”这种“迂回”的过程，既是本课学习所需，更是学习知识的一条基本道路。】

（3）验证。

师：是不是所有的数据都这样？（学生犹豫不决）再给你们一次假设的机会。

生：21千米。

师生一起计算：21÷（21÷10+21÷15）=21÷（2.1+1.4）=21÷3.5=6（天）。

师：现在你有什么想说的？

生：路的长度变了，但是合修天数不变。

●关键提问1：为什么总长度变化，合修天数却不变？

师：我用30千米和60千米为例，画了线段图。（出示下图）

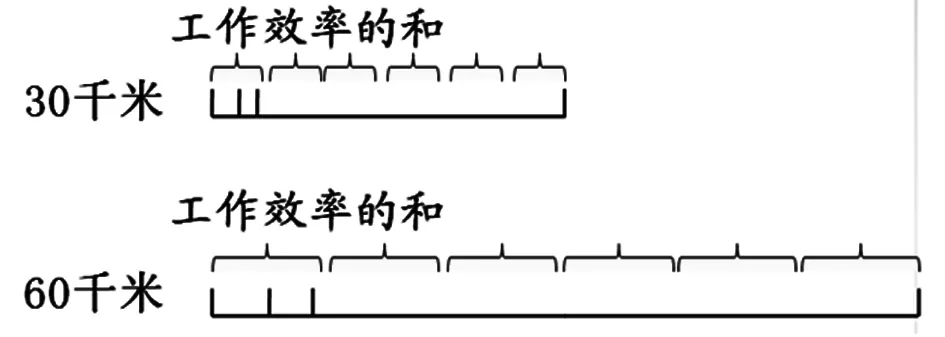
师：你有什么想说的？

生：总长度变长了，两队每天修的长度也变长了，所以合修时间不变。

生：总长度60千米是30千米的两倍，两队每天修的长度也是原来的两倍，所以合修时间不变。

师：你们很会思考。总长度变长，但是一队仍用10天修完，二队仍用15天修完，因此每天修的路程也变长。

（4）提炼单位“1”。

●关键提问2：刚才大家发现总长度变了，两队合修一天的长度也变了。那什么始终不变？

生：工作时间不变。

生：每天修的路占总长度的几分之几没变，也就是工作效率不变。

●关键提问3：刚才同学们说总长度变了，每天修的路程也要变，你却说工作效率不变，这又是什么意思？

师：既然两队合修一天的长度占总长的几分之几是不变的，那就可以把这长度看作——

生：单位“1”。

（教师在黑板上画线段图）

【解读：“是不是所有数据都这样”问题一出，学生“不是”的声音盖过了“是”。由此可见，学生心中的疑惑并没有真正解决。这是不完全归纳法的缺陷，需要足够多的数据来支撑。而且，即便有大量数据，仍无法说服个别“爱钻牛角尖”的学生。再给一次机会，学生选择了“21米”。接下来是说理过程，即演绎归纳的过程，这是本课的重、难点，通过三次关键提问实现理解。教师先以具有倍数关系的“30千米”和“60千米”为例，用线段图直观呈现总长度变、修路天数不变。接着着重关注工作效率的“变”与“不变”，即工作效率的具体量变，“分率”这一抽象量不变，再次用线段图直观演示、至此把道理讲清讲透，自然提炼出把总路程看作“1”。】

3.小结：通过计算、比较、假设、验证，最后得出结论。像这样的问题，可以把工作总量看作单位“1”来解决。

二、建立模型，解释应用

1.模块练习。

师：除了修路问题，下面还有几个问题。你们对哪个问题最感兴趣？

衣：一匹布，可以做10件上衣，或者做15条裤子，现在想做成套装，可以做几套这样的套装？

食：一袋毛豆，爸爸单独剥要10分钟，我单独剥要15分钟。现在我和爸爸合作，几分钟可以剥完这袋毛豆？

住：一个走廊，如果只铺A瓷砖要铺10块，如果只铺B瓷砖要铺15块。如果以“ABAB”这样铺，两种瓷砖分别要铺多少块？

行：从宁波到武汉，一辆汽车要行10小时，一辆货车要行15小时。现在两车分别从两地同时出发相向而行，几小时后相遇？

（学生选择后逐题出示）

师：老师发现同学们越做越开心了，为什么？

生：我发现这些题都一样。

生：单位“1”可以表示很多很多数。

生：我觉得单位“1”太厉害了。

师：你能体会到单位“1”的厉害，你也十分厉害！同学们，这就是数学，它可以把许多题变成一道题，如果你能透过这五道题看出一道题来，那么你已经具备了数学的眼光。

2.自主编题。

师：你还能编出可以用这个算式解决的问题吗？

生：给幼儿园小朋友买果冻和饼干。我带的钱可以买10个果冻，或者买15包饼干。现在把一个果冻和一包饼干作为一份礼物，我带的钱能买几份礼物？

生：我和爸爸吃面条。一碗面条，我单独吃完要15分钟，爸爸单独吃完要10分钟，现在我们俩一起吃，几分钟吃完？

【解读：“工程问题”在原实验稿教材中退隐，而在新修订稿教材中重出江湖，其意图在教师教学用书明确指出：“要以工程问题为载体，让学生经历把现实问题模型化的过程，透过各种现实表象，找出隐藏其后的数量关系。”并强调教学时要注意避免加深难度。“衣食住行”的选择，本身就激发学生的好奇心，而“越做越开心”的背后，是有魔性的单位“1”。学生自主编题，体现了他们对这“一类”问题的理解，做到了学以致用。】

三、巩固练习，发展思维

2.某地遭遇暴雨，水库水位已经超过警戒线，需泄洪。这个水库有两个泄洪口。只打开A口，8小时可以完成任务，只打开B口，6小时可以完成任务。如果两个泄洪口同时打开，几小时可以完成任务？

指挥部一开始只打开A口，3小时后发现汛情比预计的严重，于是同时打开B口，问再过几小时可以完成任务？

【解读：练习设计有层次、有变化，突出重点，在运用数量关系的同时进一步发展了学生的思维能力。】

四、总结收获（略）