解读数学阅读理解的本质与层次——从一道四年级的数学阅读理解题谈起

吴春敏

阅读是从文字、图片、符号、公式、图表等视觉材料中获取信息的过程，也是一种主动理解、感悟、吸收、鉴赏和评价的思维过程。阅读能力是个体在阅读活动中自然形成的一种基本能力，是自学能力的核心要素之一。

在当前的教育大背景下，人们开始重视且再次认识一种数学题型——“数学阅读理解题”。我区自2017年开始，在区域性学生期末学业质量测评卷中也开始将“数学阅读理解题”作为附加题出现，这既是数学题型的一种补充，也是给出一个信号，数学阅读理解题对于学生数学阅读能力的培养有不可替代的优势和价值，有助于学生数学素养的提升和发展。本文就以四年级期末卷上的一道数学阅读理解题为例，分析学生在数学阅读理解题中的“读”与“解”两方面的层次水平，阐述个人对小学生数学阅读能力培养的粗浅看法。

附加题，阅读理解。

数学史上曾经出现过用“加倍”的方法来计算稍复杂的乘法计算，比如计算17×15时可以采用右面的算法（如图1所示）：

请仔细观察并尝试用这样的方法计算13×33。

上述题目中，先提供了有关“数学史”上的利用“加倍”方法计算乘法的材料内容，再提出了对学生的考查要求：“尝试用这样的方法计算13×33”。既考查学生的阅读能力，又考查学生的限时理解能力。那么四年级的学生面对此类题目，该怎样有效地“读”，又会怎样正确地“解”呢？

一、基于“文本材料”的阅读层次解读

阅读是运用语言文字来获取信息、认识世界、发展思维的活动，阅读本身就是对语言的理解，而数学语言又包括文字语言、符号语言以及图表语言。所以对于数学阅读而言，只有熟练掌握这几种语言以及它们之间的转换，才能实现有效的阅读。

1.通读——知概况。

阅读的初始是从视觉材料中获取信息的过程。视觉材料主要有文字和图片，也包括符号、公式、图表等。上述例题中的文本材料，从视觉上分析，由“文字材料、算式材料和图示材料”组合而成，每一种材料都蕴含各自的信息容量，各信息量排序方式层层递进，给学生的阅读增加了难度，让数学阅读更富挑战性。

整个数学体系就是一个严谨的推理体系，正是因为数学具有高度的严谨性，学生在进行数学阅读时，需要“字斟句酌、咬文嚼字”。在不足50字的文字表述中，隐藏着多个关键词，如“数学史”、“加倍”、“稍复杂”、“乘法计算”、“观察并尝试”等。这些关键词传递出这一附加题的背景、题目的内容和要求、计算方法及学生学习方式的建议等。学生文本解读是存在梯度的，学生在阅读的过程中依次经历“乘法计算”、“稍复杂”、“数学史”、“加倍的方法”、“观察并尝试”等不同层次的理解。同时，算式表述和图表表述两种形式及时对文字表述进行了有效的补充，三种方式相结合有利于学生在通读过程中提取材料的基本信息。

2.细读———思关系。

乘法计算是学生已有的知识，但是利用加倍的方法进行乘法计算则是等待学生探索的新知识。阅读材料中将已有知识和新知同时呈现给学生，要求学生在对已有知识理解、归纳的基础上，捕捉新旧知识点中的相似因素，积极理解掌握新知识，灵活迁移从而应用新知解决问题。为此，学生要根据提供的材料，进一步细读材料内容，从中找出知识点之间的联系。

3.精读——寻方法。

从哲学角度解析，乘法是加法的量变导致的质变结果。这充分说明乘法是加法的特殊情况，重复进行同一个数的加法运算就产生了乘法，对这种重复计算的不同处理，就产生了不同的乘法计算方法。而例题中呈现的方法正是早在古埃及纸草书上就记载的一种乘法——倍乘法（加倍的方法），也就是先加倍计算，再组合不同倍数和从而完成计算。过程思考如下图所示：

图2

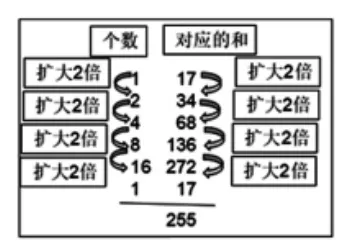
图3

图4

看似烦琐的方法，却把计算过程中的每一次思考表达得更为直白和浅显。相比较纸笔竖式计算的简练，“加倍”法的烦琐过程需要学生在阅读中更加精细地寻找方法。

学生在阅读中能否很好地把握住这一“过程的价值”？问卷设计把关注点聚焦到学生对于“图示信息”纵向每列数据的理解，以及最后一个关键步骤的理解上。

上述图示信息的阅读，需要学生非常注重对细节过程的把握，从不同方位解读计算步骤，读懂“加倍”计算方法的本质。通过联系、思考和反思，读懂最后一个步骤“组合不同倍数”，根据增减得到所需的个数。精细化的阅读能够帮助学生形成全新的认知结构。

阅读理解题的解题策略为：重点是阅读，难点是理解，关键是应用。学生在经历“粗读——细读——精读”三个层次的数学阅读时，理清内容的脉络，并对数学语言（文字语言、图示语言等）进行理解分析，最后要归纳整理出要点内容、数学思想方法进行迁移和运用，从而解决问题。这一问题解决就是阅读理解题中的“考查内容”部分，在上述例题中，学生进行了材料阅读后，进一步考查的内容为：尝试用“加倍”的方法计算13×33。

二、基于“考查内容”的阅读层次解读

材料的解答过程整体体现一种思想，只有在领悟了这一层面的基础上，才能有效地对下面的问题进行解答。阅读材料中给出的乘法计算题为“17×15”，考查的内容稍作修改，虽依旧是两位数乘以两位数，计算题则改为“13×33”。这样既保证方法的迁移，又非纯粹地模仿，是数学思想方法的提炼。

笔者刚好参与了区域阅卷，批阅了全区2000多份试卷的附加题，第一时间搜集了全区各级各类学校学生对于“13×33”的解题方法，梳理学生的“加倍法”解题过程，进一步证实“解阅读理解题的过程就是一个数学阅读理解的过程”，并根据徐小建《学生数学阅读能力层次偏低归因》一文中对于阅读类型的分类，结合学生对本附加题的解题过程进行归类。

1.被动型阅读。

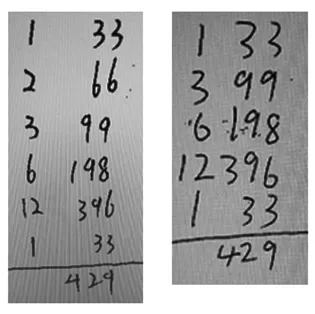
被动型阅读，即通过视觉搜索信息、接收信息，通过思维加工信息，最终理解、接受信息的阅读。首先，经过这种阅读，学生往往只能达到简单模仿水平，只能根据题目所给出的示例依葫芦画瓢，解决肤浅的问题。下图中的两种解题方式说明，在阅读中“图示信息”给学生带来最为直接的视觉冲击，学生直观还原了“加倍法”的竖式外观，达到了“形模”的层次，依葫芦画瓢地画出了竖式的外形，左边一列为加数的个数，右边一列为累计的“和”；其次，学生初步从字面上理解了“加倍”的底层含义，即因数的个数与相对应的积不断增加；第三，用常规的“纸笔竖式计算”得到13×33的积为429，并将其结果书写在竖式的最后一个步骤。学生对于题目的阅读停留在表面及机械性的记忆上，只读到“形”，没读懂“质”。

2.主动型阅读。

主动阅读型，是指在阅读过程中不是通过直接阅读接受结论，而是主动思考上文提供的材料，发现下文将要给出的结论。即不仅通过阅读获知，还通过主动加工上下文材料去发现知识，进而主动获得知识。如下图中学生的解题方式，说明学生在“材料阅读”中整体理解把握解题方法，明确了“加倍法”竖式计算中每一步所采用的思考表达、方法步骤、解题依据，从而将材料中的方法有效地迁移到考查内容的解题上来。从下图两个解题中，说明两类学生都发现了“加倍”法计算的特点，从一开始就主动思考了“加倍”的数值累计方法，其一是“2”的翻倍，即 1、2、4、8、16；其二是“3”的翻倍，即 1、3、6、12。不管哪种翻倍方式，都说明学生对于倍乘的一种自我解读。但是由于阅读材料中最后一步是通过“组合倍数”将“个数15”通过加倍后的“16-1”得到结果，这是理解的难点。而下图两种算法中，“个数13”无法通过加倍后得到“14-1”，个数33也无法通过“-1”得到结果，学生在这一环节的阅读上存在理解偏差，从而导致不同错误结果的产生。

3.创新型阅读。

创新型阅读是阅读的最高境界，是指在阅读过程中不仅主动加工阅读材料发现知识，而且还能将所学新知与原有知识结合产生新的认识和见解，提出和解决新的问题。考查内容“13×33”表示的意义有两种，即13个33相加与33个13相加。两种解读在学生的解题策略中所采用的方式会各不相同。而且由于“个数”拆分形式的不同，学生对于同一意义的解题过程呈现步骤也各不相同。

（1）“13个33相加”的意义解读与解题过程。

13×33意义之一是“13个33相加”。根据阅读材料所提示，要对13的个数进行“翻倍累加”的思维重组，于是就演变为“13”这一个数的拆分形式。鉴于“13”这个数值的特殊性，没有办法通过翻倍刚好实现，学生各显神通。

①“ 13=12+1”型。即通过“个数”的加倍法得到12个33，再增加1个33从而得到13个33，然而对于如何通过“个数加倍”得到12，材料中的“扩大2倍”的方式显然不适合考查内容，于是学生另辟蹊径，采用倒推法往前推。然而“6”的倒退方式上又有所不同，其一是按照12—6—3—2—1的方式，小步子循序渐进。其二是按照12—6—3—1的方式，在第二步骤中，摈弃材料中的“扩大2倍”的思路，大步迈进“3倍”得到“3个33为99”，再回归正途，后续依次扩大2倍，在得到12个33的基础上增加1个33从而解决问题。

②“13=16-3”型。根据材料中的加倍思维方式，依次扩大2倍，可以得到16个33，则多出3个33，根据最后一个步骤“组合不同的倍数从而完成计算”的模式，学生在“-3”的方式上进行了推陈出新。如下图所示，其一是直接减3，由于3个33为99，方便口算，学生能够直接知其结果，因此在得到16个33后，直接给出3个33的答案，进行计算；其二，在原有倍数中，找到1个与2个“对应和”，然后分别减去1个33与2个33；其三是先减去4个33再增加1个33。多种方式的个数增减，展示了学生创新型阅读带来的创造型思维。

（2）“33个13相加”的意义解读与解题过程。

13×33意义之二是“33个13相加”。根据阅读材料所提示，要对33的个数进行“翻倍累加”的思维重组，于是就演变为“个数33”的多种组合方式。

①“33=32+1”型。根据阅读材料中依次扩大2倍的“加倍”思维，可以得到32个13，距离33个13只相差1个，下图中该类学生采用“倍数+1”的方法，先加倍得到32个13，再增加1个13，计算得到结果。

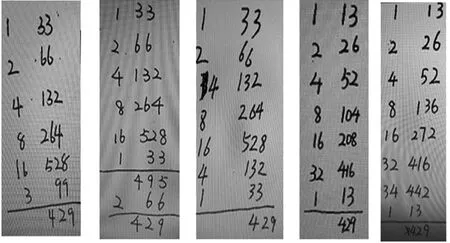
②“33=34-1”型。采用“加倍”思维，可以得到32个13，但由于材料中给出的最后一个步骤是“减去1个加数”，学生从已有的数据中得到“2个13是26”，从而对32再次进行累加，得到34个13为442，最后再减去1个13，最后得到结果。两次组合已有的倍数数据进行重新加工，最后完美解决这一问题。

可见，同样的计算方法，在不同的问题情境中，学生对于方法的类比迁移，不仅仅是形式上的迁移，还包括概括性原理的迁移，这样不仅有利于学生对于这一类方法的掌握，还可以在学生大脑中建立起知识的大纲（即知识网络系统），用方法在知识之间建立桥梁。

数学阅读理解题作为一种对终身教育极具价值的新题型，不仅仅是简单停留在解题的方法和策略上，而是多方位、多角度、多元化地评价学生的数学学习过程，是学生的数学学习能力的一种体现，是学生数学自主学习的基石，为学生数学素养的培育提供保障。