例谈数学习题设计如何做到“小题大做”

林庚禄

数学习题是课堂教学的延伸和拓展，习题不但是教师检验和评价课堂效果的方式，更重要的是学生通过习题的练习可以巩固和内化新知。好的习题可以使课堂教学事半功倍，有利于学生新知的掌握，促进思维的发展；不好的习题，将是枯燥无味的机械重复，自然事倍功半，抑制了学生学习的积极性。所以，我们在设计习题时，应做到难易适中，明确设计意图，真正做到“小题大做”，使习题作用最大化，更好地服务于学生的学习。

一、突破思维定势，学会逆向思考

平常习题的呈现方式，都是以图文或纯文字的形式出现，即出示已知条件与问题，要求学生列式解答。教学时发现，如果打破常规，先有列式，再要求说明列式表示的意义时，学生普遍感觉不习惯，有的甚至束手无策。

例如：学校口琴兴趣小组有男生20人，女生有15人，根据列式（20-15）÷20，写出它表示什么意义。看似简单一道题，学生也犯难，这是定势思维对学习的影响。正是由于小学生习惯了先有问题，再有列式的解题方式，形成了一定的思维定势，所以我们要突破这种思维定势，多设计一些先有列式，再要求说明表示意义的习题。这种从列式入手说意义的习题，有利于学生理清数量关系，内化解决实际问题的方法，同时达到训练学生逆向思维与融会贯通的能力，提高解决问题的能力。

当然也可以设计根据算式补充适当的条件或问题的习题。

又如：小军有邮票36枚，小军的邮票比小明多，______________？

以上练习都可以从不同的角度促进学生思维的发展，使分数问题的解决方法得到内化，并形成解决问题的数学模型，且应用于实际解决问题中。

当然，也可以根据列式让学生编题。例如：根据列式 120×（1+）、120×（1－）等编写出相关分数实际问题，促进学生知识的内化。让学生看着列式编题目，赋予枯燥的算式具体、生动的情境，让学生在编题目中进一步明晰算理，让计算不再是为算而算，在坚守“数学味”的同时，给予学生个性发挥想象的空间，使他们体会到呆板的算式背后的丰富内涵和魅力。

二、注重新旧联系，促进形成知识体系

建构主义学习理论指出：有效的数学学习应是联通各知识之间的关系，正确把握知识之间的因果关系，将有联系的或将同一类的知识点组成一个模块，建立整体认识，形成一定的完整知识体系。

例如：在学习多边形面积计算时，可以设计以下习题。

该习题把三种多边形编排在一起，激发学生回顾与反思三种图形面积公式的推导过程，明白三种图形的面积推导都是利用转化的数学思想方法，将旧知识转化为新知识得到的，较好地将平行四边形、三角形和梯形等面积计算方法产生联系。该习题要求学生明确：决定多边形面积大小的因素，包括底和高。学生通过观察题干，发现三个图形都在同一组平行线间，说明了它们的高相等，要比较三者的面积就只要考虑它们的底即可。再由于三角形和梯形的面积都需要底乘高除以2，只有平行四边形的面积不需要除以2，很容易就判断出平行四边形的面积最大。通过该练习题让学生感受到在没有完整告知每一个图形的具体长度情况下，也照样能比较出不同图形面积的大小。这样的习题练习既巩固了多边形面积的计算方法，又理清了图形面积计算的差异，使得学生对数学知识有进一步深刻的理解，并逐渐建立多边形面积计算的整体认识，形成一定的完整知识体系。

三、注重说理，展露思维过程

《数学课程标准（2011版）》指出：评价不仅要关注学生的学习结果，更要关注学生在学习过程中的发展和变化。因此，在习题的设计时，我们要改变习题中问题的呈现方式，不要一味地只有列式解答和填空，更多一些“写出你的理由”，“请你写出你的思考过程”等，以此充分展露学生的思维过程。

例如：在测量角的度数时，可以设计如下图这类习题：

学生完成情况：

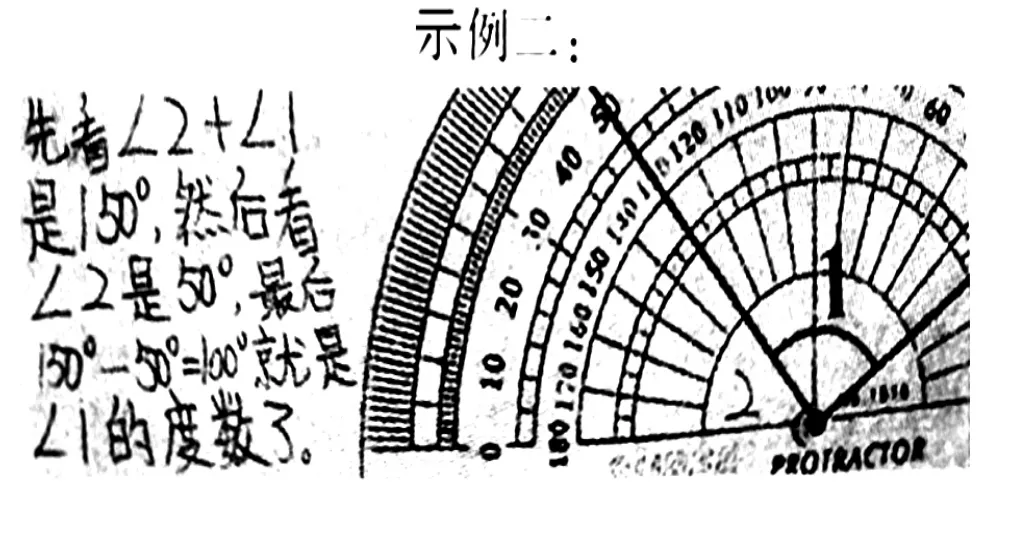
以上习题设计不再是只让学生看图得到角的度数，更重要的是，要求学生写出“我是这样想的”。通过让学生写理由来展露学生的思维过程，可以帮助学生进一步理清角度量的知识，促进对知识本质的深刻理解。

又如：学习了《乘法结合律》后，可以设计：

a×b×c=a×(b×c)，这是乘法结合律。那么，在除法中，是否同样存在 a÷b÷c=a÷ (b÷c)呢？请说明你的理由。

再如：学习了《分数的基本性质》后，可以设计：

根据分数与除法的关系，你能用除法中商不变的规律来说明分数的基本性质吗？请举例说明。

学生要较好地完成每道说理题，离不开一定的训练。这就要求教师要改变教学理念，课堂教学要做到学习过程与学习结果并重，课堂中多问几个“为什么”“说说你是怎么想的”等，摒弃教师“一言堂”的教学方式，提倡尊重平等交流的“对话”式教育，留给学生更多课堂“独白”的时间和思维空间，真正做到“知其然而更知其所以然”，最大限度地启发学生的智慧潜能。

习题是学生掌握基础知识和开展技能训练与形成技巧的重要手段,也是积累基本活动经验和渗透数学思想的有效方法。每一道习题都承载着设计者的教学意图和思想，要想真正发挥小习题、大作用，就需要我们设计者高标准、严要求，设计好每一道题目。