让学生“做”数学

刘金波

建构主义认知理论认为，学习不应被看成是对教师所讲授的知识的被动接受，而是学习者以自身已有的知识和经验为基础的主动建构活动。数学学习更应如此，因为数学具有抽象性，学生理解起来不那么容易。为此，数学教学可通过典型例子的分析和学生的自主探索活动，使学生理解数学知识形成的过程，体会其中蕴含的思想方法，追寻数学发展的历史足迹，把数学的学术形态转化为学生易于接受的教育形态。这也就是我们所说的“做”数学，即数学教学形式由灌输变为主动建构。

例如，教学四边形内角和的度数时，教师首先提问：三角形内角和为180毅，那么四边形内角和会是多少度？学生在独立探索的基础上分组交流与研讨，并汇总解决问题的方法。

方法一：用量角器量出四个角的度数，然后把四个角加起来，发现内角和是360毅。

方法二：用两个相同的三角形纸板拼成一个四边形，发现两个三角形内角和相加是360毅。

接下来，教师在方法二的基础上引导学生利用作辅助线的方法，连结四边形的对角线，把一个四边形转化成两个三角形。小组交流后，学生运用几何画板演示并验证得到的方法。

得到四边形的内角和是360毅之后，学生们又认真地讨论起五边形、六边形的内角和。类比四边形的讨论方法，学生最终得出五边形的内角和是540毅，六边形的内角和是720毅。

这样教学，学生在探究问题的过程中发现知识，经历数学知识的形成过程，从而得出结论，完成“做”数学的过程。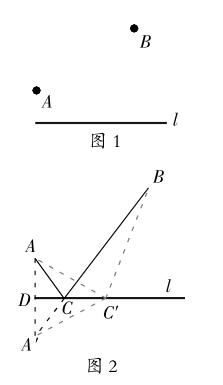

让学生“做”数学，还包括学生会应用数学知识解决实际问题。也就是说，我们既要让学生知道数学知识从哪里来，又会到哪里去，即数学知识的应用过程。因此，在数学教学中，教师还应指导学生用数学的观点观察社会、思考问题，培养学生应用数学的意识，真正做到学以致用。

例如，在复习轴对称的知识时，教师不妨提出数学名题———将军饮马问题。

唐朝诗人李颀的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河。”诗中隐含着一个有趣的数学问题。

如图1所示，诗中将军在观望烽火之后从山脚下的A点出发，走到河边饮马后再回到B点宿营。请问怎样走才能使总的路程最短？

解决这个问题并不难，但要用到今天所学的轴对称知识。如图2所示，从A点出发向河岸引垂线，垂足为D，取A点关于河岸的對称点A忆，连结A忆B，与河岸线l相交于C，则C点就是饮马的地方。将军只要从A点出发，沿直线走到C点，饮马之后，再由C点沿直线走到B点，所走的路程就是最短的。

因为如果将军在河边的另外任一点C忆饮马，所走的路程就是AC忆+C忆B，但是，AC忆+C忆B=A忆C忆+ C忆B>A忆B=A忆C+CB=AC+CB。

可见，在C点外任何一点C忆饮马，所走的路程都要远一些。

这有几点需要说明：（1）由作法可知，河流l相当于线段AA忆的中垂线，所以AD=A忆D。（2）由上一条知：将军走的路程就是AC+CB，就等于A忆C+ CB，而两点确定一条直线，所以C点为最优。这样就将轴对称知识用活了。

（作者单位：岳阳县荣家湾镇城关中心学校）