图形直观运用于解决问题策略教学初探
佟学唬
(常州市新北区三井实验小学,江苏常州 213001)
孔凡哲教授认为,在小学阶段,实物直观、简约符号直观、图形直观、替代物直观作为几何直观具体表现的四种形式。在解决问题策略专项教学中,图形直观发挥着重要作用。图形直观是以明确的几何图形为载体的几何直观,用直观图描述问题,本文通过策略教学中图形直观应用的呈现形式为切入点进行描述分析,体现图形直观在教学中的价值作用。
1 解决问题策略教学中图形直观应用呈现形式
1.1 巧用线段图,感受图形直观描述分析问题价值
发展学生的几何直观是数学课程标准提出的重要课程目标之一。学生可以借助图形直观理解数学,把复杂数学问题简明、形象呈现,探寻解决问题的思路和方法。线段图是利用图形直观描述分析问题的最直接方式,形象生动的联系条件与问题,从而直观分析数量关系达到实际问题解决的效度。
小宁和小春共有72 枚邮票,小春比小宁多12 枚。两人各有邮票多少枚?

图1
学生根据题意把线段图填写完整,画图表示题中的条件和问题,再画出表示小宁和小春邮票枚数的线段。分析数量关系时得出一种方法是两人邮票的总数减去12 枚,等于小宁邮票枚数的2 倍,先算出小宁有多少枚?另一种方法是两人邮票的总数加上12 枚,等于小春邮票枚数的2 倍,先算出小春有多少枚?教师引导学生比较两种解法的相同点和不同点,认识到两种不同的解题思路,本质上都要先设法使两人邮票数量同样多。学生体会到画线段图能使数量关系更直观、更清楚,根据分析数量关系,容易找出解题思路。
1.2 基于直线图,依托图形直观列举解决实际问题
学生经历运用图形直观列举解决实际问题的过程,感受列举策略的特点和价值,从而增强分析问题的条理性和严密性。教学中可以引导学生写好量的名称,然后逐一连线表示出列举情况,利用图形直观列举时确保思考过程的有序性,列举的结果做到不重复、不遗漏。
南山中心小学举行小学生足球赛,有4 支球队参加,分别是红队、黄队、绿队和蓝队。如果每两支球队比赛一场,一共要比赛多少场?
首先理解“每两支球队比赛一场”的意思是两支球队之间只进行一场比赛,也就是说每支球队要分别与其他3 支球队赛一场。教材安排两种方法一是列举出各场比赛,比如红—黄、红—绿、红—蓝、黄—绿、黄—蓝、绿—蓝,另一种方法是通过画图列举:

图2
教师提示学生通过画图进行思考需要先画4个点表示4 支球队,再用每两点之间的连线表示球队之间所进行的比赛,连线有几条,就有几场比赛,直线图列举能更为直观清晰。
1.3 擅用示意图,根据图形直观感悟直观思想方法
学生在运用画示意图策略解决问题过程中,感受借助图形直观分析数量关系,确定解题思路的方法,逐步培养学生运用画图策略的意识。借助画图策略解决问题,需要根据实际问题的特点,选择恰当示意图清楚准确的揭示条件和问题的联系,便于分析数量关系,确定解题思路。
梅山小学有一块长方形花圃,长8m。在修建花园时,花园的长增加了3m,这样面积就增加了18m2。原来花圃的面积是多少平方米?根据题中的条件和问题,要求学生想到“花圃的长增加了3m”的含义,同时要求原来花圃的面积,先要算出它的宽的思路。学生用图示表示原来的花圃,表示条件和问题,两条长边都要增加3m,宽不变。再画出增加的18m2,同时把所求问题在图中标出来。

图3
根据示意图分析数量关系,要求原来花圃的面积,要先算它的宽是多少米?原来花圃的宽,就是增加的小长方形的长,增加的面积是18m2,宽3m,可以求出它的长,最后用长乘宽等于面积。
1.4 创用个性图,依据图形直观提升假设应用能力
学生在解决问题过程中可以依据题意采用假设策略,分析实际问题的数量关系,积累解决问题的经验,学生根据实际问题的条件和问题,提出合理的假设,达到化繁为简的目标,初步形成解决问题的策略意识,从而将复杂问题转化为简单问题。
小明把720mL 果汁倒入6个小杯和1个大杯,正好都倒满。已知小杯的容量是大杯的小杯和大杯的容量各是多少毫升?

图4
理解题中的数量关系是6个小杯的容量+1个大杯的容量=720mL,小杯的容量是大杯的大杯的容量就是小杯的3 倍。教师引导学生理解假设把720mL果汁全部倒入小杯,明确1个大杯可以看作3个小杯,所以720mL 果汁正好可以倒满9个小杯。求出1个小杯的容量后,再求出1个大杯的容量。
2 图形直观运用于解决问题策略教学的价值体现
2.1 运用图形直观,明朗梳理数量关系
小学数学教学中解决实际问题策略教学是学习的重点又是学习的难点,其中分析数量关系在整体教学过程中处于关键地位,教师可以运用图形直观帮助学生理解抽象的数量关系,引导学生用直观图形和符号把数学问题的数量关系表述出来,从而清晰化、可视化、直观化解决教学关键问题,充分体现图形直观价值。
如在教学苏教版《数学》三年级上册“解决问题的策略”(从条件想起)这一内容时,教材精心安排了“学生折花”这一问题情境:“绿花有12 朵,黄花的朵数是绿花的2 倍,红花比黄花多7 朵。红花有多少朵?”教材按照“理解题意-图形直观描述-厘清数量关系-灵活算法解答-回顾反思”的板块流程能够较为准确清晰的帮助学生了清解题思路,教学中发现个别学生的思考过程往往代替大多数同学对数量关系的理解,不能清楚理解题意背后所隐藏的数量关系,所以教学中为让学生更好把握数量关系,笔者在运用图形直观理解题意是指出 “能用你喜欢的方式把题中的条件和问题表示清楚吗?”学生把自己能够想到的思路过程方法表示出来:

表1 表格图
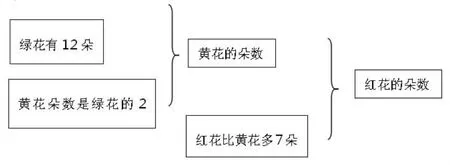
表5 方格图
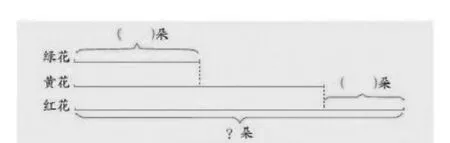
图6 线段图
在给学生充足的时间后,引导学生对比呈现资源后发现线段图是呈现题意理解最清楚、最直观的方式,当学生全程经历图形直观表征过程后,重点条件的理解和数量关系的理解更为清晰,借此可以列式解决问题,同时便于学生回顾解决问题思路,整体理解数量关系。
学生根据题意可以用自己喜欢的方法把题中的条件和问题进行整理,分析后再利用数量关系可以根据前两个条件,先求出黄花有多少朵?求出黄花的朵数后,就能求出红花的朵数。教师引导学生把自己的想法勇敢的呈现出来,对比后发现用线段图的方法能够将题中的数量关系表示得更清楚。
2.2 运用图形直观,明晰建构数学模型
模型思想是 《义务教育数学课程标准(2011年版)》中明确提出的十大“核心词”之一,主要是指从现实生活或具体情境中抽象出数学问题,用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律,求出结果并讨论结果的意义。
如在教学苏教版《数学》五年级下册“用转化的策略解决问题”这一内容时,教材呈现计算时,观察后发现4个分数连加,每个加数的分子都是 1,分母是有规律排列的,依次是 2,2 ×2,2 ×2 ×2,2 ×2 ×2 ×2。学生掌握规律后进行解题思考后呈现多种方法,教师收集资源后对比:
(1)按顺序计算:
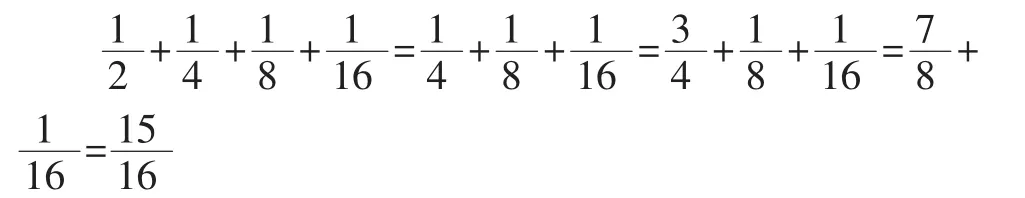
(2)通分计算:
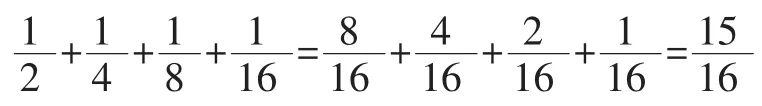
(3)转化计算:

教师引导学生把正方形看作单位“1”,把算式中的加数填入图7。
空白部分占大正方形的几分之几?把算式和图形联系起来思考,由于空白部分是大正方形的涂色部分是大正方形的(1-),原来的算式可以转化为1-回顾解决问题的过程,我们遇到较为复杂的计算时,先要认真分析算式的特点,让学生把复杂的算式可以转化成简单的算式,更能提示学生画图可以找出转化的方法,认识到画图是实现转化的关键环节。

图7
2.3 运用图形直观,鲜明增强符号意识
《义务教育数学课程标准(2011年版)》中明确提出符号意识是指能够理解并且运用符号表示数,数量关系和变化规律;知道使用符号可以进行运算和推理,得到的结论具有一般性。建立符号意识有助于学生理解符号的使用是数学表达和进行数学思考的重要形式。
如在教学苏教版《数学》五年级上册第96 页“练一练”,小强、小华和小丽是好朋友。如果他们每两人之间通一次电话,一共要通多少次电话?如果他们互相寄一张节日贺卡,一共要寄多少张贺卡?学生基于以往的经验运用符号意识中的符号对题意进行列举,呈现的内容过程展现出来:
(1)文字法:
小强-小华 小强-小丽 小华-小丽
(2)字母法:
把小强看作A,小华看作B,小丽看作C。
A-B A-C B-C
(3)图形法:
把小强看作○,小华看作△,小丽看作□。
○-△ ○-□ △-□
3 结语
通过方法呈现比较后不难发现文字法、字母法、图形法依次递进后,用图形法来表示多个量之间的关系既能清楚地表达出题目中的数量关系,又能简洁的表示出对题意的理解,因此说明解决问题时运用符号意识来思考,能够提高解题速度,提升学生的思维能力。

