混合算法在4G地震勘探网络定位中的应用
李婧婷,亢俊健,李明亮
(河北地质大学 河北省光电信息与地球探测技术重点实验室,河北 石家庄 050031)
0 引 言
在日益复杂的国际环境下,能源的勘探和储备能力将面临巨大挑战,其中利用地震波进行地质勘探逐渐成为主流技术。传统的有线地震勘探仪器成本较高、HSE风险值大,不能更好适应复杂地形的深层勘探[1];目前正处于发展阶段的基于WIFI传输的[2,3]无线地震勘探设备传输速率低、无法实施监控、抗干扰能力差等。鉴于4G通信高速率、低损耗的特点以及未来5G技术的快速发展,将成熟的移动通信技术作为一个模块直接嵌入到地震勘探设备中将成为发展趋势之一。
基于4G通信的地震勘探仪器除了能够利用GPS定位系统,还可以结合网络定位组成A-GNSS定位技术,不仅可以提高定位精度,还可解决野外环境下GPS卫星数较少或信号失锁[4]等情况。为进一步优化地震勘探仪器网络定位精度,本文将对到达时间差(TDOA)技术做进一步研究。TDOA技术常用的经典求解算法,如CHAN算法、TAYLOR算法都各自存在着一些缺点[5],于是近年来,很多研究将现代启发式算法应用于TDOA技术的求解问题中。
遗传算法[6]求解高维TDOA问题精度不高、收敛时间较长。PSO算法适合求解此类问题,精度较高,收敛速度快,但是情况不稳定,容易陷入局部最优[7]。鉴于差分算法较强的全局搜索能力,本文提出的基于协作式的差分粒子群混合算法(DEPSO)[8-10]能够平衡全局搜索能力和局部勘探能力,加速收敛,提升算法效率。本文在TDOA定位优化问题的基础上,将PSO算法和DE算法分别改进后有机融合为DEPSO算法,仿真结果显示定位性能有较大的提升,为4G地震勘探仪器的研究奠定基础。
1 TDOA定位模型
1.1 基本原理
通过多个基站接收到从移动台发射出的电磁波信号,解析得到的时间差确定移动台所在位置的方法被称为到达时间差(TDOA)定位,也被称为双曲线定位[11]。其基本原理如图1所示,当3个基站位置已知时,与移动台之间的距离差r1、r2、r3可通过时间差确定,根据几何原理可以得到分别以服务基站BS1、相邻基站BS2为焦点,r1-r2为焦距的双曲线1和以服务基站BS1、相邻基站BS2为焦点,r1-r3为焦距的双曲线2,移动台就位于两条双曲线的交点处,根据相关先验信息,即可得到移动终端的真实位置。
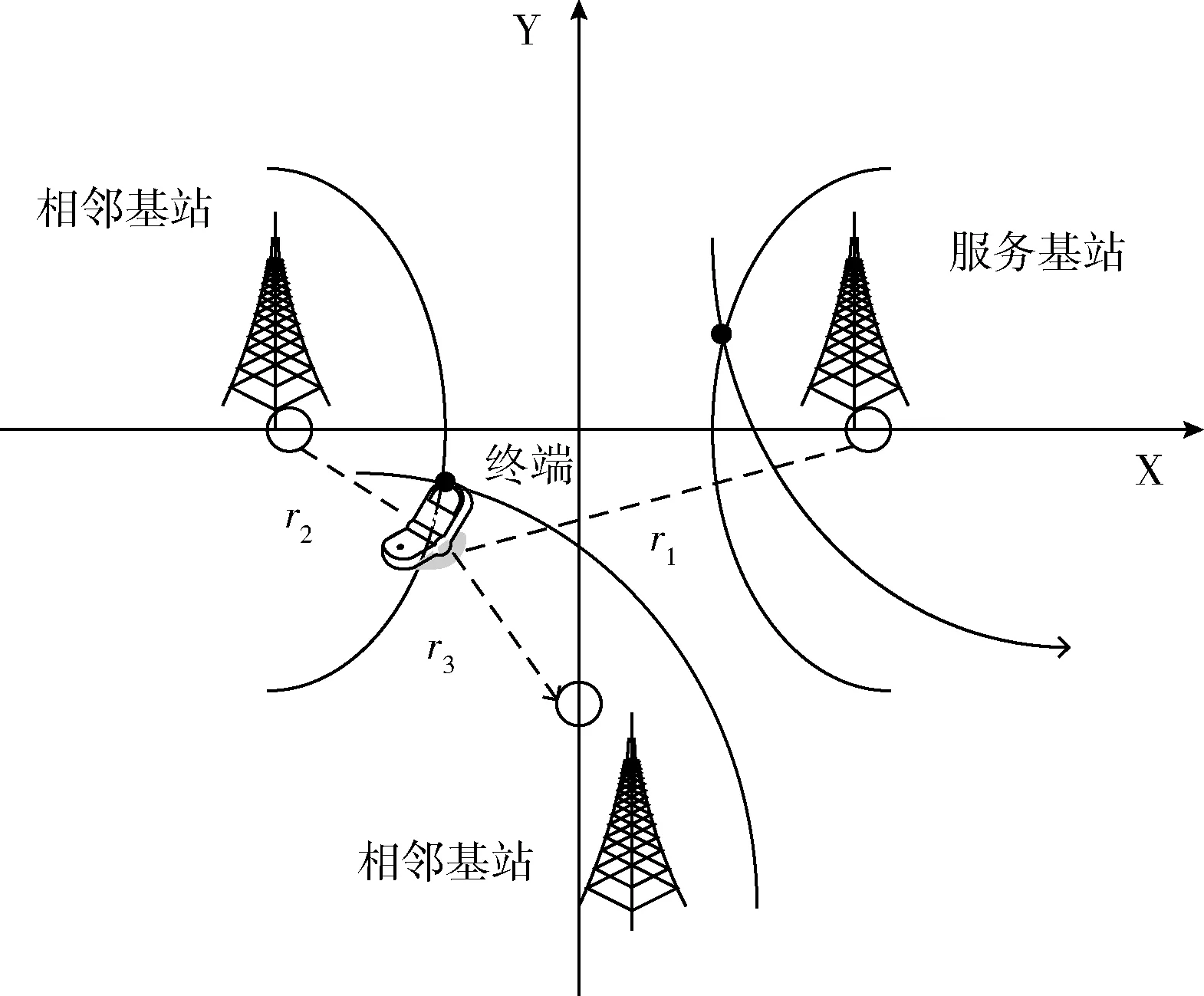
图1 到达时间差原理
1.2 数学模型

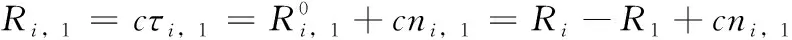
(1)
式中:c为电磁波传播的速度,τi,1为时间差测量值,由相关实验结果表明,测量差值ni,1通常可认为是独立同分布、服从N(0,σ2)的高斯白噪声。
根据距离公式,则式(1)可展开为
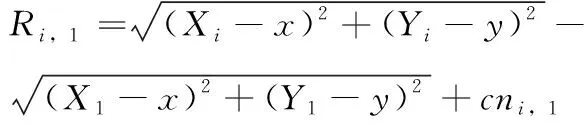
(2)
求解移动台位置坐标问题,即求解多维非线性方程组,如式(3)
(3)
根据之前的假设,可用最大似然估计移动台坐标(x,y)。其中向量n服从均值为零、方差为σ2的正态分布函数,各测量值相互独立,则向量ΔR中任一元素服从均值为Ri,1,方差为σ2的正态分布函数,所以对应的最大似然函数为
(4)
求使最大似然概率最大的坐标值,相当于求解
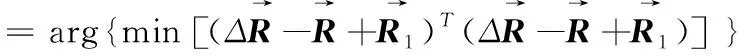
(5)
其中,通过移动台所在小区ID获得移动台所处位置范围[xmin,xmax]和[ymin,ymax]。
以上分析可知,移动台位置坐标求解问题本质上是最优化问题,若通过常用的解析法求解,不仅计算量巨大,而且必要条件难以获得。很多研究表明,启发式搜索算法对于求解最优化问题效率较高,可通过多次迭代靠近最优值。因此本文通过差分粒子群混合算法在整个潜在空间搜索最优解,确定移动台坐标。
2 基于DEPSO的4G地震勘探设备定位优化算法
2.1 标准粒子群优化算法(PSO)
PSO作为非线性优化算法首先在目标搜索空间中投下种群大小为NP个粒子,初始化每个粒子的速度向量vi和位置向量xi,在每一次迭代中,每一个粒子根据式(6)更新其速度向量vi和位置向量xi,从而确定飞行方向和位置,Gm次迭代后,通过比较适应度值大小,选出最优个体
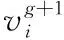
(6)
其中,i=1,2,…,NP;g为迭代次数;c1、c2为加速常数,通常取值为2;r1、r2通常取值为[0,1]区间内的随机数,记为rand();ω为惯性权重,是整个算法中较为重要的参数,直接影响PSO的全局搜索能力,于是本文采用一种非线性指数递减惯性权重策略,如下
ω=ωmin+(ωmax-ωmin)exp(-λ(g/Gmax)2)
(7)
式中:ωmax通常取值为0.9,ωmin通常取值为0.4;而λ为控制因子,取值为3。
从式(6)中可以看出速度向量vi和位置向量xi的更新除了依赖于上面给出的变量外,还主要受到两个极值的影响:pibest记录每一个粒子的最优位置,gbest记录所有粒子中的最优位置,其中,gbest实际就是pibest在每一代中的最优值。
标准粒子群优化算法(PSO)不同于遗传算法(GA),其结构简单、收敛速度较快、鲁棒性强,但是在处理多峰值优化问题时,受到个体最优值的影响,容易陷入局部最优,从而导致精度受限。
2.2 差分进化算法(DE)
DE是由Stron等提出的基于实数编码的全局优化启发式算法[12]。其基本思想类似于遗传算法,首先在目标搜索空间中随机生成Np大小的初始种群,然后通过变异、交叉、选择等操作,优胜劣汰选出较优个体进入下一代,最后通过比较适应度值大小,得到最优值。
(1)变异。变异是差分进化算法中较为重要的部分,其中被广泛使用的4种策略如下:DE/best/1,DE/current-to-best/1,DE/rand/1,DE/rand/2,从左到右,DE的局部搜索能力逐步降低,全局搜索能力依次增强,收敛速度逐步变慢。鉴于下文的差分粒子群混合算法,在本文实验中选择全局搜索能力较强的DE/rand/1策略
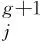
(8)
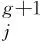
λ=e1-(Gm/(Gm+1-G)),
F=F·2λ
(9)
xr1、xr2、xr3是第g代中分别从种群中随机取出的3个不同个体,这使得DE算法不能同时使用种群的邻域信息和方向信息来引导搜索[13,14],为了进一步提高DE算法的性能,提出一种基于细胞拓扑的领域结构。将种群网格化,每一个格子是一个个体,围绕在其周围的格子就是这个个体的方形邻域,可通过个体的邻域来构造上述基向量和差分向量。
首先,在某个个体的邻域中随机选择一个个体作为基向量xr1,根据xr1的适应度值将邻域其余个体划分为优组和劣组,在优组中随机选择一个个体作为差分向量xr2,再从劣组中随机选择一个个体作为差分向量xr3,根据式(8)得到中间向量变异个体。
与传统DE算法相比,基于邻域结构的DE算法缩小了个体的信息交流范围,只在相关邻域中搭建信息共享平台,加速收敛,并且通过方向信息可以指引算法搜索到更优区域,兼顾算法全局和局部搜索能力,提升算法性能。
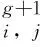
(10)
CR为交叉因子,计算公式如下
(11)
其中,CRmin=0.3,CRmax=0.9,β=5。
(3)选择。选择适应度值f较好的个体进入下一代
(12)
DE具有较强的全局搜索能力,但后期收敛较慢,为提升工作效率,提出基于DEPSO的TDOA定位算法。
2.3 基于协作式的差分粒子群混合算法(DEPSO)
本文提出的DEPSO算法实现步骤如下:
初始化:PSO算法参数:vi、xi、c1、c2、ωmax、ωmin、λ;DE算法参数:F、CRmin、CRmax、β、领域半径、NP、Gm。
(1)TDOA定位问题建模,计算适应度值
(13)
(2)将种群划分为不同区域的P种群和D种群;
(3)根据式(6)~式(7)对P种群更新粒子的速度和位置,得到个体最优pibest和全局最优值gbest;
(4)根据式(8)~式(12)对D种群每个个体变异,交叉,选择,得到最优值Dbest;
(5)将P种群的粒子的适应度值与D种群个体的适应度值逐一比较排序,用D种群中的适应度值较大的个体替换相同数量的P种群中适应度值较小的粒子,并更新对应粒子的适应度值为下一代进化做准备;
(6)比较每一代中gbest和Dbest值,记录最佳个体,决定下一代的进化方向;
(7)进入下一代,检查是否达到最大迭代次数,如若没有,跳转到步骤(3)继续执行;否则,结束运行,输出最大适应度值以及对应的最优坐标值,计算均方根误差。
3 仿真与分析
3.1 仿真条件
为了测试上述算法的性能,本文通过MATLAB软件在高斯白噪声的环境下对该算法就不同的基站个数、测量误差、小区半径、信噪比进行仿真,并与经典算法进行比较。
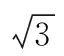
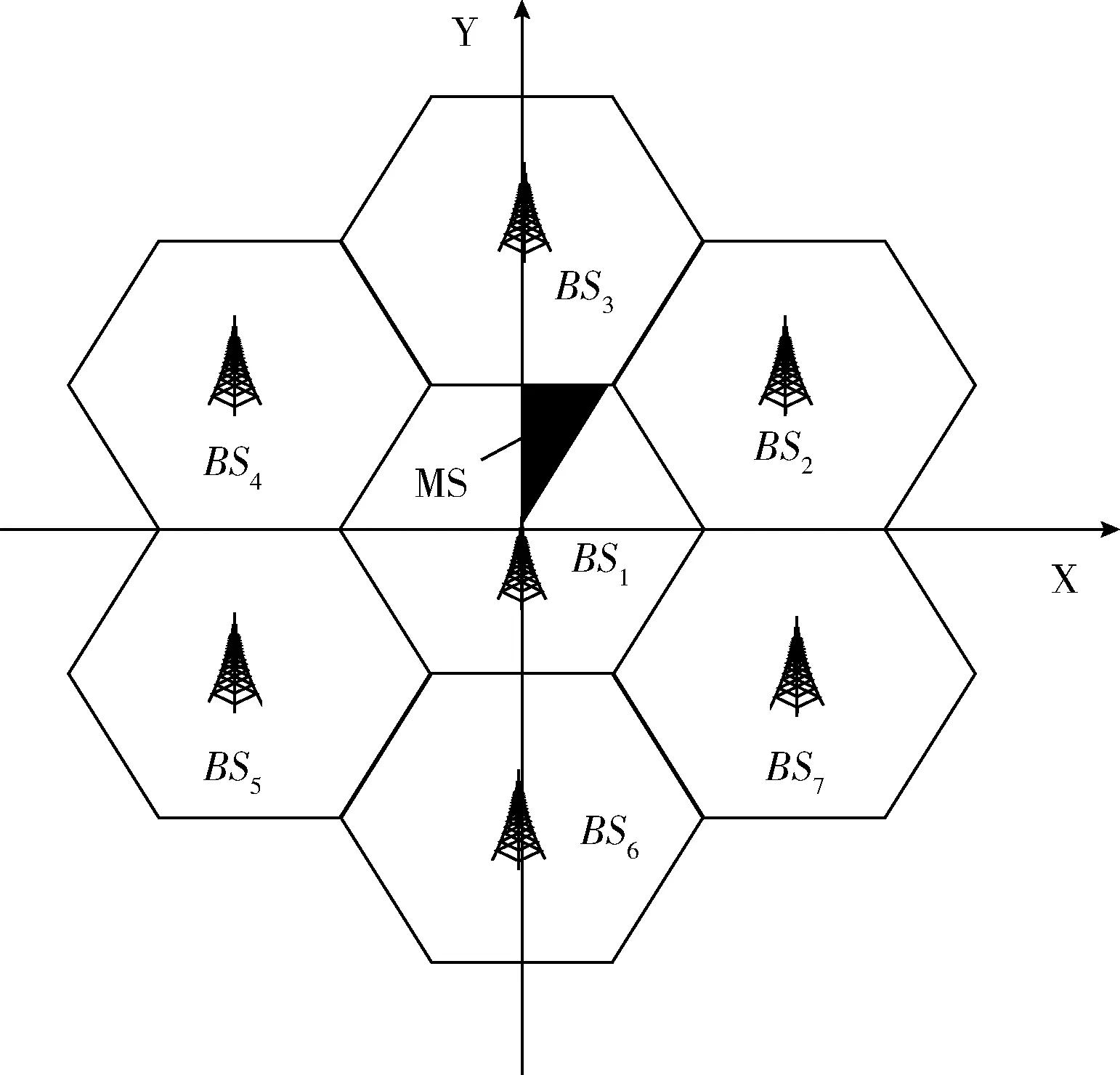
图2 7小区蜂窝网系统
其它仿真参数:种群大小:100;最大迭代次数:80;独立运行次数:10 000次;评价指标:均方根误差
(14)
3.2 仿真结果分析
(1)参数设置:测量误差:90 m;小区半径:3000 m;基站个数:6个。表1为相同条件下,DEPSO算法和DE算法关于定位精度和迭代系数的比较。结果表明混合算法在精度方面略微提高,但相对DE算法后期收敛较慢的问题有所改善。
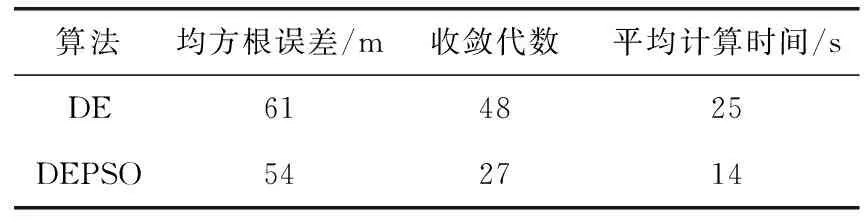
表1 混合算法和差分进化算法实验结果比较
(2)参数设置:基站个数:6个;小区半径:3000 m;TDOA测量误差:[30 60 90 120 150]m。
图3为不同的测量误差下算法的定位性能。结果表明,3种经典算法中,Taylor算法、Chan算法定位性能明显优于IS算法,所以后面的研究主要是和前两种经典算法进行比较;鉴于经典算法易受到噪声二次项的影响,两种启发式算法的定位误差明显优于经典算法,对定位性能有明显改善;在误差较大的情况下DEPSO混合算法更为稳定,且性能优于PSO算法,更为适合野外环境下的网络定位。
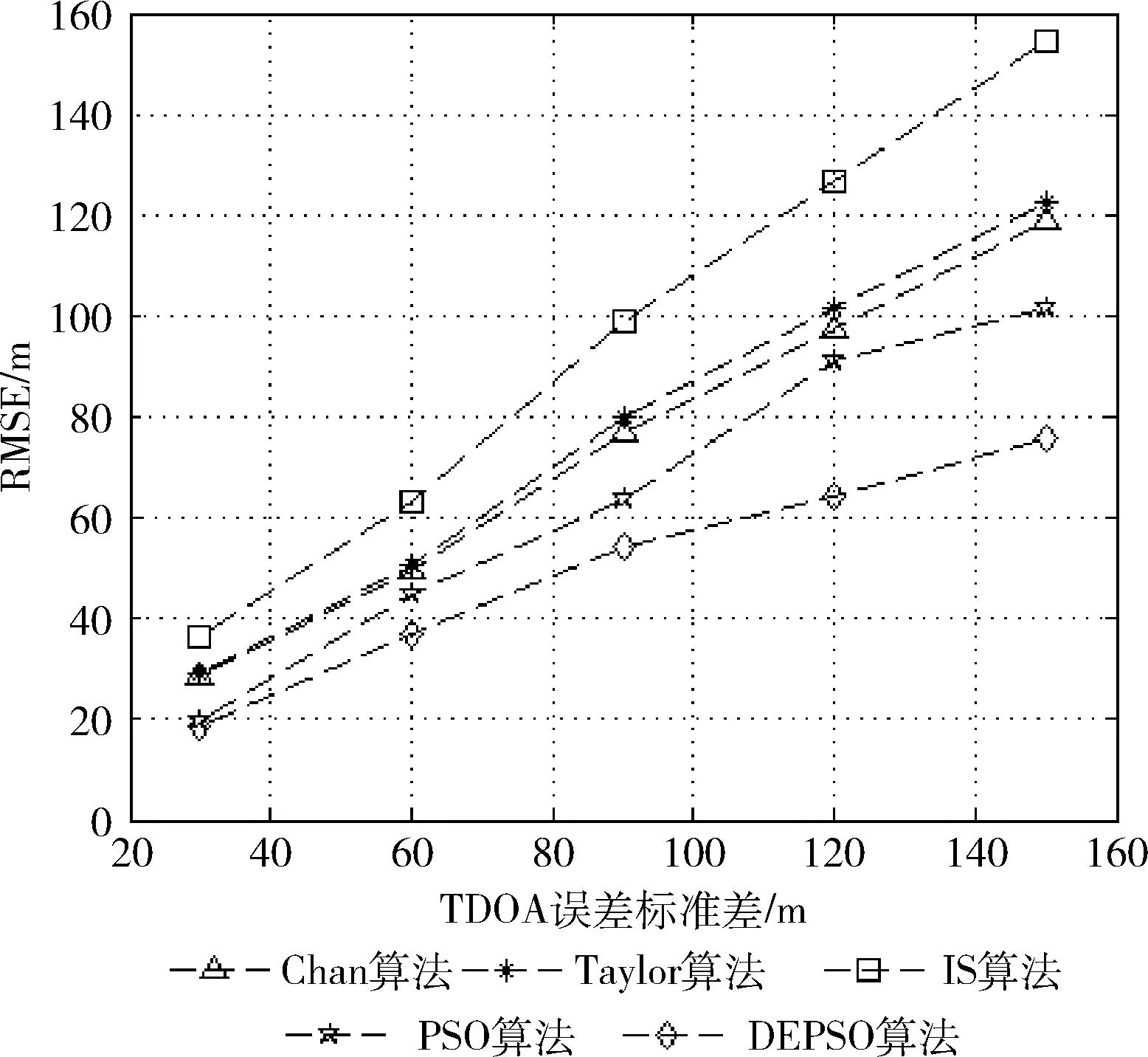
图3 测量误差对定位性能的影响
(3)参数设置:测量误差:90 m;小区半径:3000 m;基站个数:[4,5,6,7]个。图4为不同的基站个数下算法的定位性能。结果表明,随着基站的个数增加,可利用的计算信息增加,4种算法的定位误差都相继降低;总体来看,本文提出的DEPSO算法在不同的基站个数下定位性能最优。
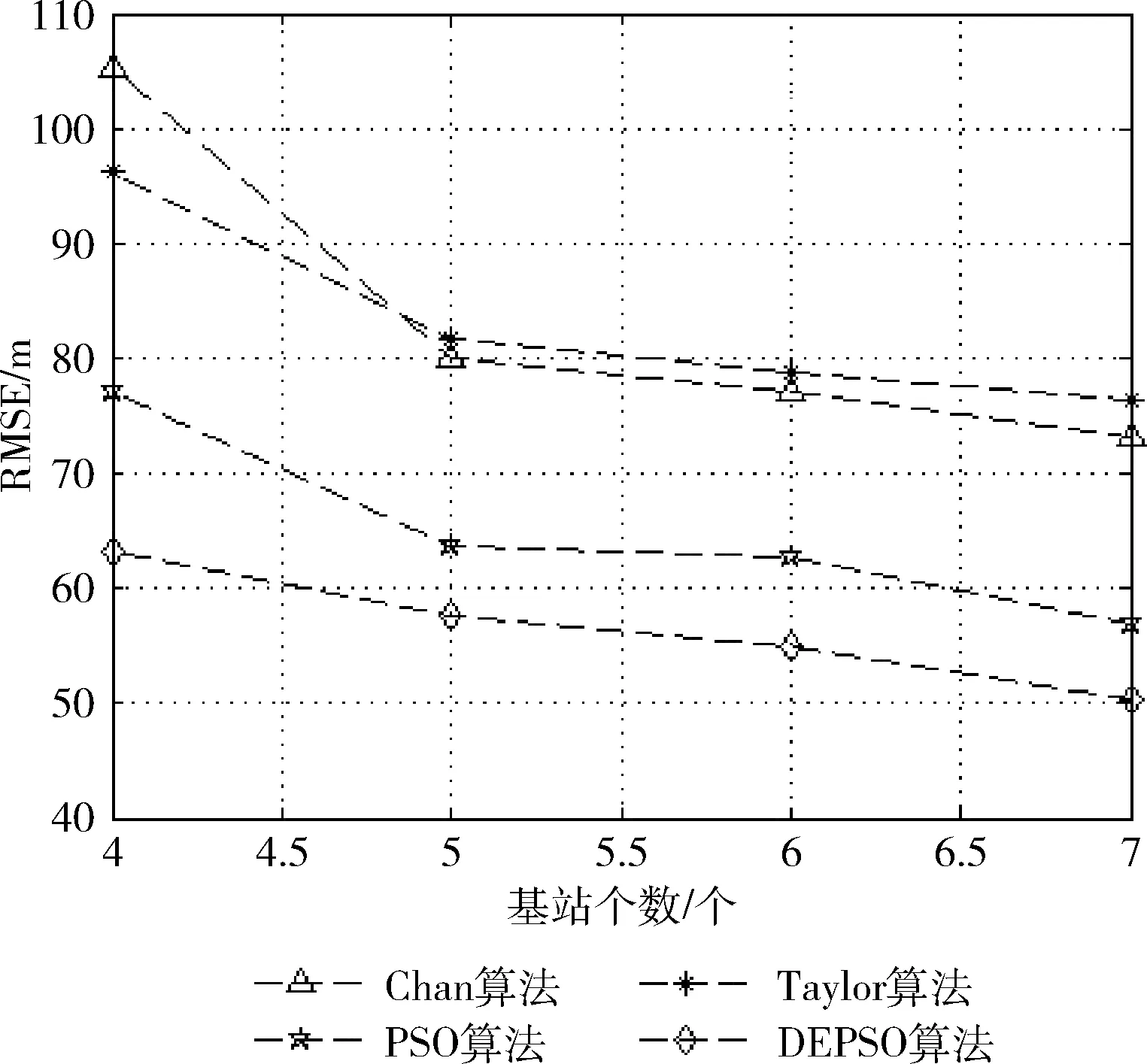
图4 基站个数对定位性能的影响
(4)参数设置:测量误差:90 m;基站个数:6个;小区半径:[2000,3000,4000,5000]m。图5为不同的小区半径下算法的定位性能。结果表明,鉴于实际野外的情况,并没有考虑非视距传输,于是4种算法对小区半径的变化不敏感,定位误差只是小范围内浮动;但是相比而言,DEPSO算法误差最低,性能较好。
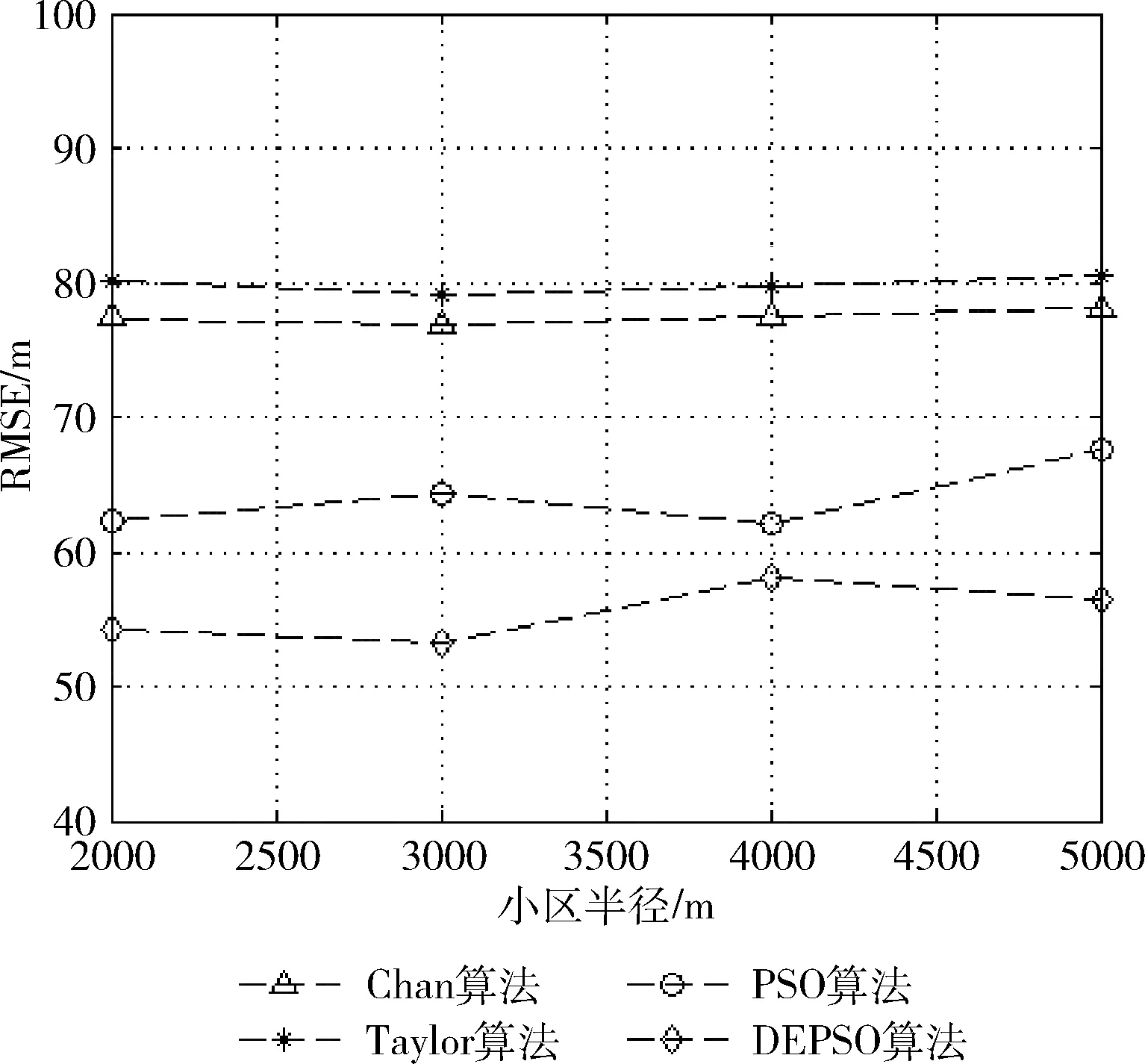
图5 小区半径对定位性能的影响
(5)参数设置:不考虑测量误差;基站个数:6个;小区半径:3000 m。图6为不同的信噪比下算法的定位性能。结果表明,随着信噪比逐渐增大,4种算法的抗干扰能力变强,定位精度变高;但总体来看,DEPSO算法的抗干扰能力优于其它3种算法,精度最高。
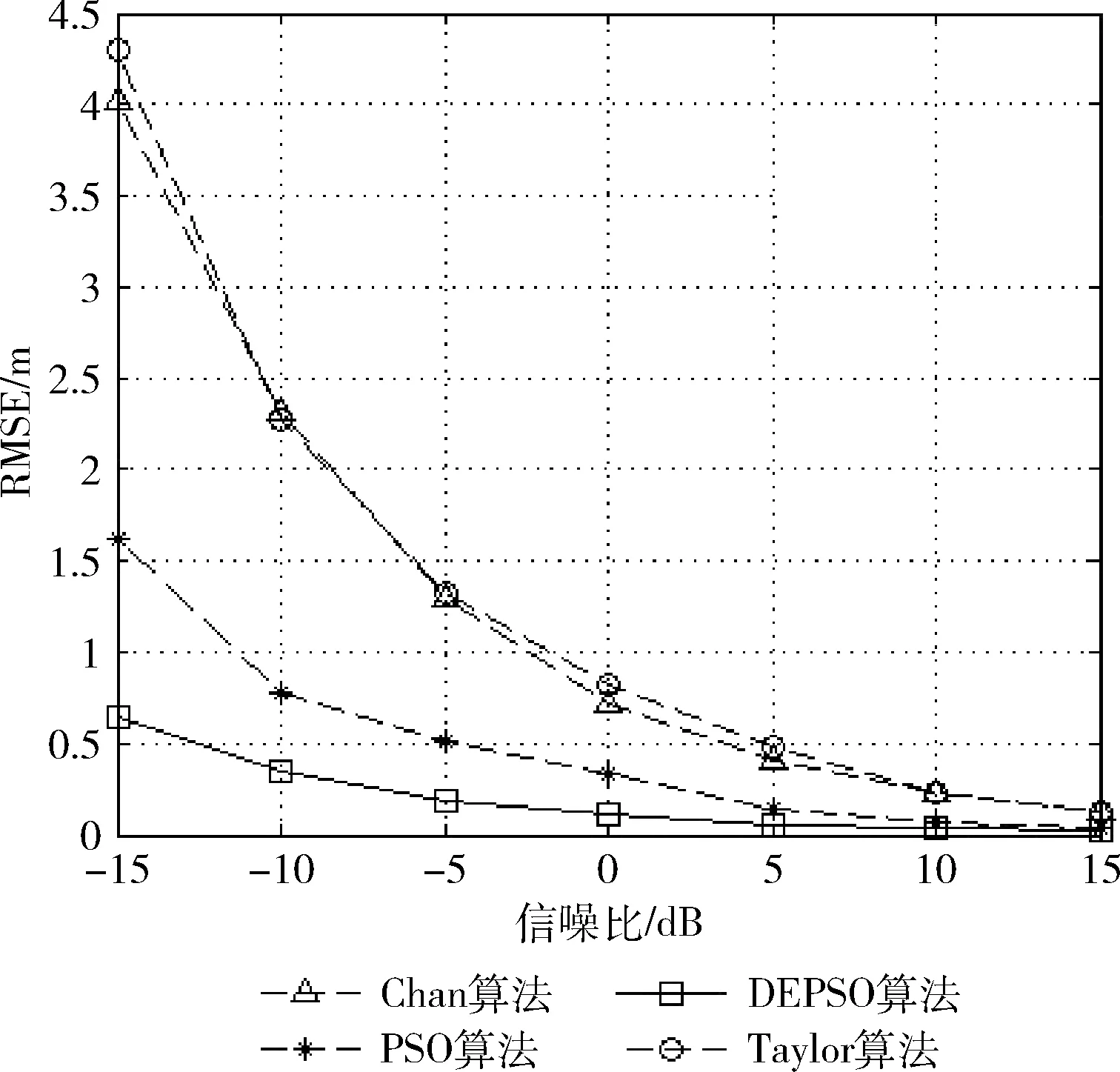
图6 信噪比对定位性能的影响
4 结束语
本文研究了基于4G地震勘探设备的网络优化问题,以移动台坐标最大化似然估计为优化目标,设计了一种差分进化粒子群优化算法(DEPSO)。仿真结果表明,该混合算法有效改善了粒子群优化算法易陷入局部最优的问题,通过算子优化和加入邻域信息有效提升差分进化算法的收敛速度,平衡全局搜索和局部勘探能力,提升定位精度。因此,该算法相比于TDOA定位问题经典求解算法,有效提升了TDOA的定位性能,进一步提升了4G地震勘探仪器的竞争力和有效性,相信未来对于基于4G甚至是5G通信技术的地震勘探仪器还有更广泛的研究。

