基于深度学习与运动信息的动作识别算法

吴志攀，郑中韦

(1.惠州学院 信息科学技术学院，广东 惠州 516007；2.广东工业大学 计算机学院，广东 广州 510006)

0 引 言

不同应用领域对于人体动作识别的要求存在差异[1,2]，例如：机器人需要识别用户的动作作为指令，而此类动作一般为小幅度的手势动作[3]；视频网站需要识别人体的不同动作与行为，从而有效地将视频进行分类，便于视频的管理，而此类视频一般分辨率较低，并且数据量极大[4]。在未来的应用场景中，需要动作识别技术既具有识别小幅度动作的能力，并且能够高效地处理大规模数据集，然而，目前的诸多动作识别技术均无法同时满足上述两个要求，这为动作识别技术的实用性带来了不利的影响。

根据目前的研究成果，可看出基于多特征融合的人体动作识别算法优于单一特征的算法，因此多特征融合的动作识别算法成为了当前的主流。文献[5]设计了基于深度图像的动作识别方法，该算法对深度图像在3个投影面系中进行投影，对3个投影图分别提取Gabor特征，使用这些特征训练极限学习机分类器，该算法的计算效率较高，但对于小幅度的动作识别性能不理想；文献[6]提出了一种可以完成在线人体动作识别的时序深度置信网络，该模型解决了目前深度置信网络模型仅能识别静态图像的问题，但该模型训练过程的处理时间较长，影响了该算法对于大规模数据集的应用性能。除了对于大规模数据集的时间效率问题。人体小幅度的动作识别则是另一个难点，文献[6]提出一种基于加速度轨迹图像的手势NMF(非负矩阵分解)特征提取与识别方法，该算法通过建立加速度手势轨迹图，将未知手势轨迹特征转换为低维子特征序列，提高了手势识别的准确率与时间效率；文献[7]通过非对称的系统偏差建模人体动作信息，该算法引入姿势标签机制进一步提高了小幅度动作的识别性能。算法[6,7]对小幅度动作(例如：手势、微动作等)均实现了较高的识别准确率，但是需要分析的特征量较大，难以应用于大规模数据集。

为了同时满足大规模数据集与小幅度动作的识别，设计了基于多特征融合与运动信息的人体动作识别算法。该算法学习了手工特征与深度学习特征，手工特征采用了改进的密集轨迹(IDT)[8]，深度学习特征采用了基于运动信息的卷积神经网络[9]，利用核支持向量机的泛化能力将两种特征进行融合。核极限学习机包含两层：第一层计算两个特征核，并将两个特征核融合获得一个融合特征核，最终输出3种特征核的预测分数；第二层训练分类器，将所有的预测得分映射至最终的动作分类。该算法的手工特征与深度学习特征具有互补性，从不同的角度描述了视频的人体动作信息。

1 相关知识

1.1 极限学习机模型

假设{xi,ti},i=1,…,n为训练数据集，其中n是训练样本的数量，xi∈Rd是提取的特征，即IDT(密集轨迹特征)与DLF(基于运动信息的深度学习特征)，ti∈Rq是真实动作类，其中q为动作的分类总数量。假设隐藏层的激活函数为G(x)，隐藏层共有L个神经元。将随机生成的第j个隐藏层权重与偏差分别表示为aj与bj，将连接第j个隐藏层节点与输出节点的权重向量表示为βj∈Rq。极限学习机的学习目标是最小化训练误差，并且最小化输出权重的泛数

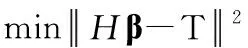
(1)

式中：H={Hij}={G(aj,bj,xi)}，i=1,…,n，j=1,…,L，H是隐藏层的输出矩阵，Hij是第j个隐藏层节点的输出，xi表示一个隐藏层节点。式(1)中β=[β1,β2,βL,]T，H(xi)=[h1(xi),h2(xi),hL(xi)]，T=[t1,t2,tn]T。

根据文献[10]，可通过下式求解式(1)

β=H+T

(2)

式中：H+是矩阵H的Moore-Penrose广义逆矩阵。原始的极限学习机理论是为了解决单隐藏层前馈神经网络(SLFN)的问题，后来许多研究人员将极限学习机推广至非神经网络问题中，并且证明了极限学习机的约束条件少于支持向量机与最小二乘支持向量机[11]，这是本文采用极限学习机的动机。

极限学习机的主约束优化问题定义为下式

约束条件为

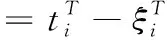
(3)

式中：i=[ξi,1,ξi,2,…,ξi,q]T是q个输出节点对于样本xi的训练误差向量，C是正则化参数。根据库恩塔克条件[12]，可将对偶优化问题转化为下式

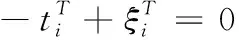
(4)

式中：α=(I/C+HHT)-1T是拉格朗日乘子矩阵。

最终的输出权重β计算为下式

β=HT(I/C+HHT)-1T

(5)

因此可将极限学习机输出函数定义为下式

f(xj)=h(xi)β=h(xi)HT(I/C+HHT)-1T,j=1,…,n

(6)

1.2 核极限学习机

与支持向量机相似，可将核函数集成至极限学习机中。参考文献[12]，给定一个满足Mercer定理的核函数K，可将核极限学习机的输出写为以下的兼容公式

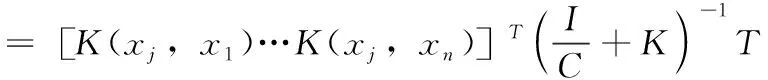
(7)

式中：j=1,…,n。在该处理之后，极限学习机的分类器输出一个得分，该得分表示一个视频属于一个动作分类的显著性。

2 本文算法

2.1 双层核极限学习机

本文核极限学习机的框架分为两层，如图1所示。第一层将深度学习的特征核与手工特征核进行特征融合处理，第一层的输出是3个特征核的预测得分。第二层训练出分类器，该分类器将所有的预测得分映射到最终的动作分类中。

2.1.1 特征核的融合

将不同的特征核融合，能够包含视频不同维度的特征。因此，本文结合了手工特征核与深度学习特征核，并且采用L2泛数计算线性核。可将一个线性核矩阵定义为下式

K(xi,xj)=h(xi)hT(xj)

(8)

式中：K(xi,xj)是K的第(i,j)个元素。通过计算不同特征源的核矩阵平均值，计算融合的特征核。特征核融合之后，分别获得3个核：深度学习特征核、手工特征核、融合特征核。然后，采用核极限学习机计算不同特征核的预测得分。

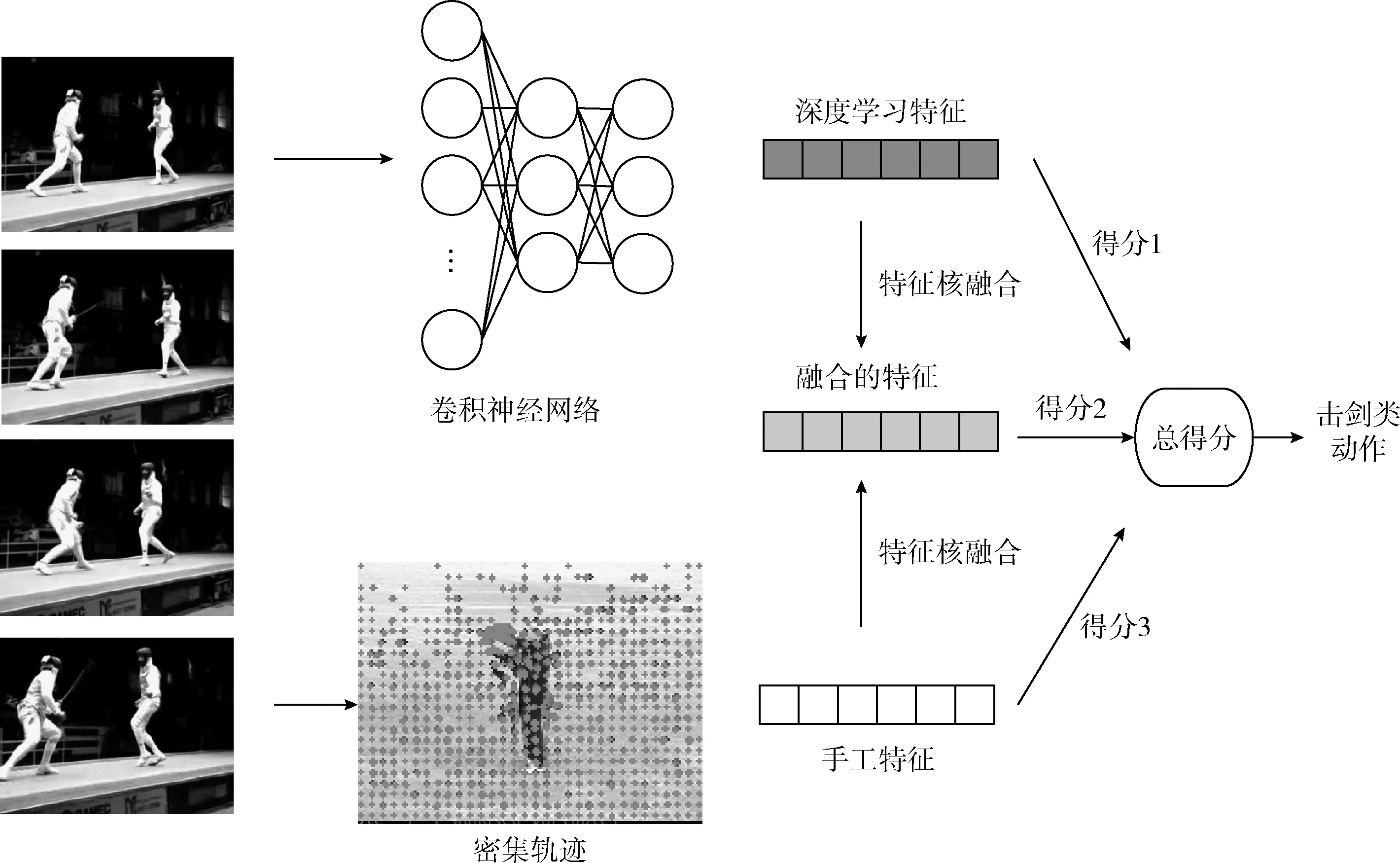
图1 本文核极限学习机的框架

2.1.2 预测得分的融合

假设可将预测得分合并计算出视频序列最终的动作分类，因此，本文3个输出得分向量融合为一个得分向量s。假设{si,ti},i=1,…,n表示训练数据集，其中n为训练样本的数量，si∈R3q为合并的预测得分，q是动作分类的总数量，ti∈R3q是真实的动作分类。考虑将第一层的输出作为输入第二层的特征，本文使用L1泛数对第一层的输出做正则化处理，之后，本文获得每个视频的一个特征向量，在第二层计算核矩阵。因为径向基函数核对于L1范数特征的性能优于线性核，所以本文采用径向基函数核，径向基函数核(RBF)定义为下式

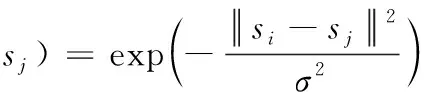
(9)

式中：si与sj分别是视频i与j的预测得分。注意K(si,sj)是RBF核K的第(i,j)个元素，参考文献[13]的结论，非线性核对于基于直方图特征的性能优于线性核。

2.2 算法的实现方案

(10)

式中：nd设为4，表示共有4个不同的描述符，即轨迹线、HOG(描述静态特征)，HOF(像素绝对运动特征)，MBH(像素相对运动特征)。

对于深度学习特征，本文设计了基于运动信息与卷积神经网络的深度学习特征，在下文详细描述。使用文献[15]方案将深度学习特征组织成一个4096维的视频描述符，并对该描述符使用L2范数处理。然后，计算深度学习特征的线性核，建立深度学习特征的核矩阵Kd。

在核融合过程中，通过计算深度学习特征Kd与手工特征Kh的平均值获得核融合的结果：K=(Kd+Kh)/2。

最终，本文的核极限学习机使用3个特征核对输入的视频流进行动作分类处理，3个特征核分别为：手工特征核、深度学习特征核与融合核。

采用开源的核极限学习机代码库实现本文的两层核极限学习机算法，在通过网格搜索获得核极限学习机参数之后，将另外两个未知参数分别设为：C=1，σ=10[16]。

3 基于运动信息的深度学习特征

本文针对人体动作识别提出了一个运动信息表示方案，强调了不同时域运动信息的显著性，从而提高视频序列中小幅度动作的判别性。该模块的总体架构如图2所示。

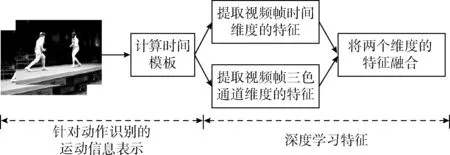
图2 基于运动信息的深度学习流程

3.1 针对动作识别的运动表示方案

时间模板能够提取一个图像帧的全部运动序列，因此本文的运动识别采用时间模板。时间模板的计算方法是统计视频运动信息的加权调和值，并且采用视频帧之间的差异计算帧之间的运动信息，时间模板的计算公式如下

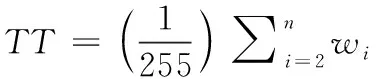
(11)

其中：n表示视频帧的数量，m(i)表示第i个帧的运动信息，wi表示第i个帧的权重值(设为灰度值)，权重的范围为[0,255]。

对式(11)进行变换，可获得下式

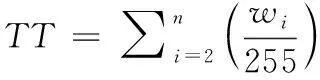
(12)

将式(12)的wi/255(取值范围为[0,1])替换为一个模糊隶属函数μ(i)(取值范围为[0,1])，可获得下式

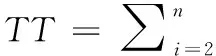
(13)

从式(13)可看出，wi决定了时间模板中分配到第i个帧运动信息的显著度，该机制能够通过选择合适的模糊隶属函数μ(i),增强时间模板中时域运动信息的显著性。图3是4个隶属函数的图形，将4个隶属函数设为μ1～μ4，分别定义为式(14)～式(17)

μ1(i)=1, ∀i∈[0,n]

(14)

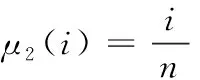
(15)

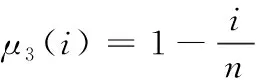
(16)

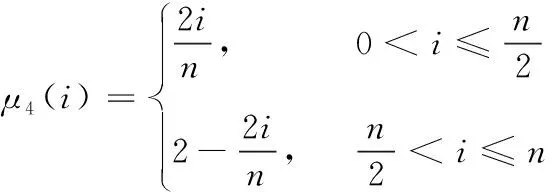
(17)

从图3中可观察出：μ1计算运动能量图像(MEI)，μ2计算运动历史图像(MHI)。因为μ1是一个恒定函数，所以MEI为所有时域的运动信息分配相等的权重。μ2是一个线性递增函数，所以MHI为最近的视频序列分配最高的显著度。μ3是一个线性递减函数，所以μ3为最近的视频序列分配最低的显著度。μ4则为时域中间区域的视频序列分配最高的显著度。最终，函数μ2、μ3、μ4分别强调时域的开始、结尾与中间区域。

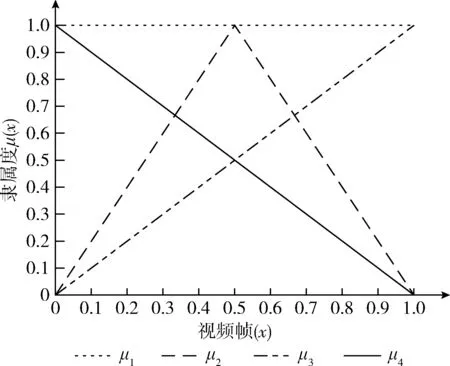
图3 4个模糊隶属函数的图形

3.2 基于深度学习的特征描述

采用卷积神经网络(CNN)学习人体动作的特征。将3.1小节中视频序列的时间模板输入卷积神经网络中，学习人体动作识别的特征集。本文使用5C-2S-5C-2S的CNN架构提取深度学习特征，其中5C表示每个卷积层共有5×5个核，2S表示每个max-pooling(最大池化)下采样层需要2×2个核。RGB彩色视频序列包含颜色通道模式与时间深度模式，因此本文将两个维度的模式分别进行处理，最终计算统一的人体动作特征。因为极限学习机具有较强的泛化能力，所以采用极限学习机进行动作识别处理。

4 仿真实验与结果分析

为了综合评估本算法的性能，分别对UCF101视频数据集与NATOPS视频数据集进行了实验。UCF101数据集的分辨率较低，数据量较大，能够测试本算法对于大规模数据集的识别性能。NATOPS视频数据集的分辨率较高，共包含24个动作，这些动作均为人体上肢的动作，动作幅度较小，并且有些动作的上肢与身体出现重叠，该数据集能够测试本算法对小幅度动作的识别效果。

4.1 UCF101数据集的实验

4.1.1 数据集介绍

UCF101数据集收集于互联网，数据集的复杂度较高，视频均具有明显的背景杂波。UCF101包含了13 320视频剪辑，共有101个动作分类。本文使用数据集缺省的3个训练集-测试集划分方案，对于每个划分方案，从25个分组中选择7个视频序列作为测试序列，其它的18个视频序列作为训练序列。图4是UCF101数据集的部分实例图像。

图4 UCF101数据集的图像实例

对UCF101数据集缺省的3个划分方案均进行实验，将3组数据的平均值作为最终的实验结果。

4.1.2 算法的识别准确率

为了评估本算法对于UCF101数据集的识别性能，将本算法与其它动作识别算法进行比较，分别为：基于卷积神经网络的动作识别算法(CNN)[9]、基于改进密集轨迹的动作识别算法(IDT)[8]、基于深度学习的动作识别算法(C3D)[15]、基于光流与卷积神经网络的动作识别算法(CNN_T)[17]、基于时域运动信息与支持向量机的动作识别算法(SVM)[15]。不同算法的动作识别率结果如图5所示，可看出CNN_T、SVM与本算法的识别率优于CNN、IDT与C3D这3个算法，CNN_T、SVM与本算法均属于多特征融合的识别算法，而CNN、IDT与C3D均为单一特征的识别算法，可得出结论：多特征融合的识别性能优于单一特征的识别性能。此外，本算法的识别率略优于CNN_T、SVM两个算法，本算法与SVM算法较为相似，主要区别在于本算法设计了基于事件模板的运动信息机制，该机制能够有效地提高动作识别的精准性。

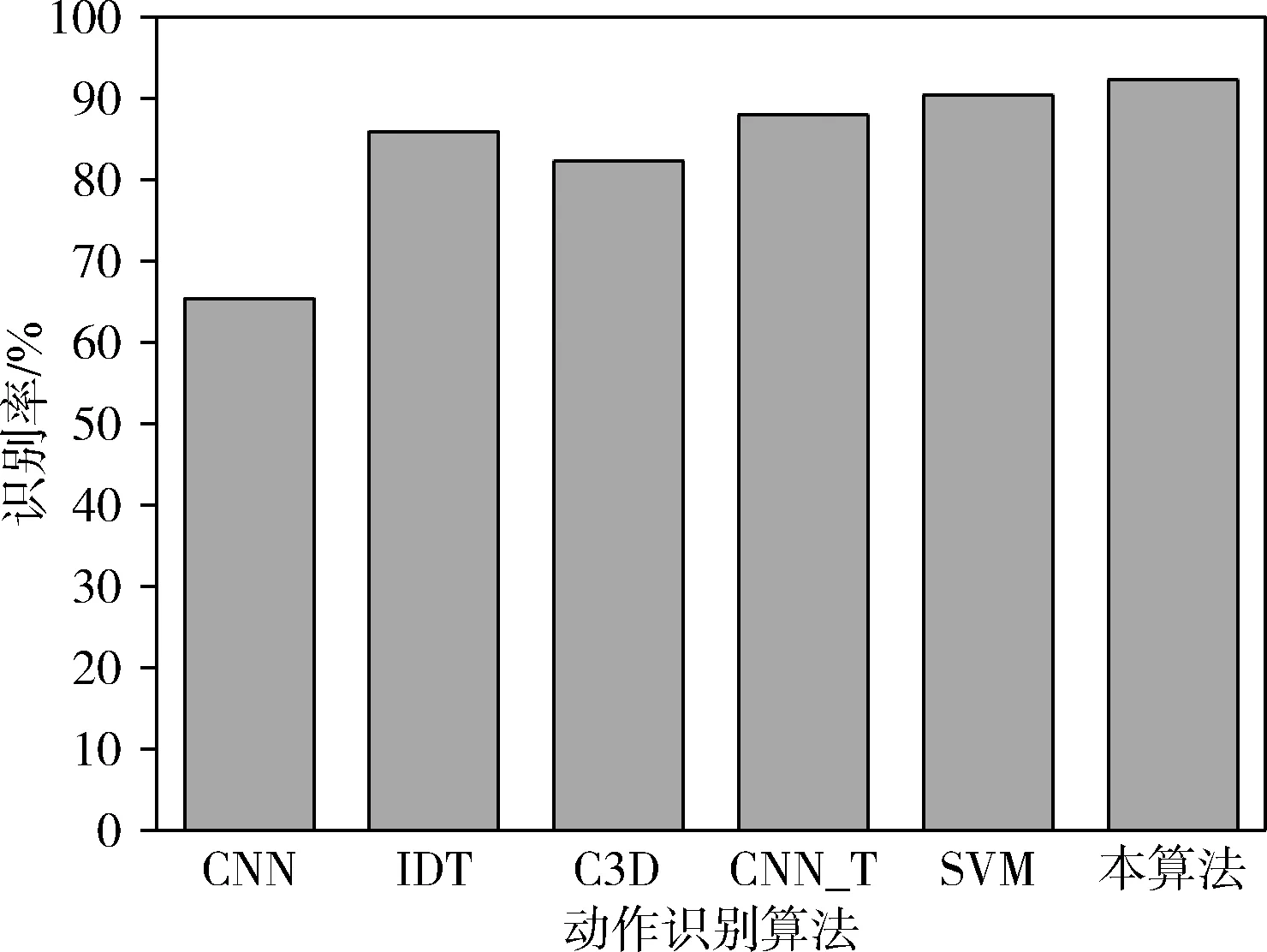
图5 6个动作识别算法的动作识别率结果

4.1.3 两种融合策略的性能比较

当前的特征融合策略主要分为早期融合与后期融合两种策略，早期融合策略在分类器处理之前进行特征核的融合，后期融合策略首先每种特征的得分向量融合为一个得分向量，然后对得分向量再一次进行分类器处理，图6是两种融合策略的流程。评估两个特征的不同融合策略对动作识别算法性能的影响，在UCF101数据集进行了实验分析。参考文献[18]的分析，基于特征核的算法性能优于其它类型的识别算法，因此，将本算法与其它基于核的识别算法进行比较。

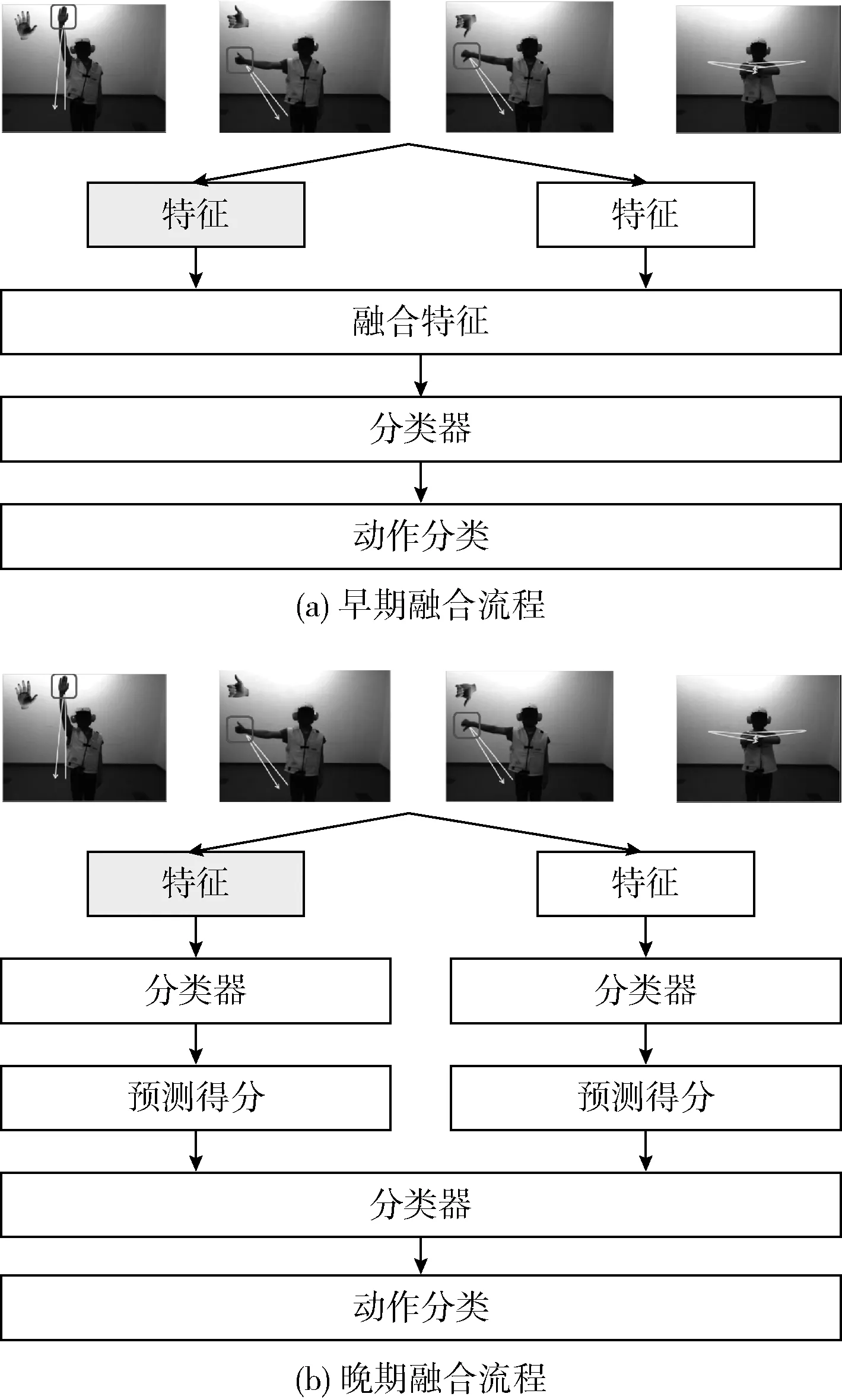
图6 两种融合策略的流程

对SVM[15]与本算法均进行两种融合策略的实验，结果见表1。从表1中可看出：①对于SVM与本算法，早期融合策略的识别准确率均优于后期融合策略；②本算法两种融合策略的识别准确率均优于SVM算法。

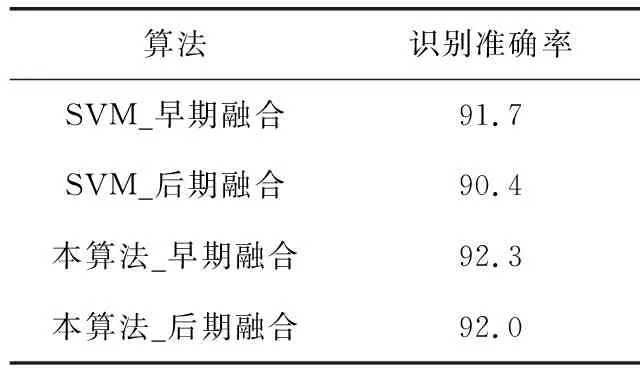
表1 SVM与本算法在不同融合策略下的识别准确率

4.1.4 算法对大规模数据集的时间效率

根据文献[12]的实验与分析结论，极限学习机具有较快的学习速度。基于大规模UCF101数据集进行实践效率的实验，并将本算法与其它基于多核融合的算法(SVM算法)进行比较。实验环境为：Inteli7 3.3 GHz CPU，16 GB内存。

图7是SVM算法与本算法训练过程与测试过程的计算时间，本算法的训练过程平均计算时间为33.98 s，测试过程的平均计算时间为15.47 s。SVM算法训练阶段的时间是本算法的4倍以上，而SVM算法测试阶段的时间是本算法的1.8倍以上。可得出结论，本算法的计算效率优于同样基于核融合的SVM算法，本算法的计算时间能够适用于大规模数据集。

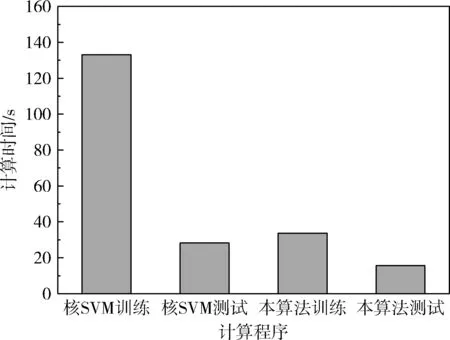
图7 SVM算法与本算法训练过程与测试过程的计算时间

4.2 NATOPS视频的动作识别实验

4.2.1 数据集介绍

NATOPS视频数据集的分辨率较高，共包含24个机场的手势信号动作，24个小幅度动作如图8所示。图8中可看出，这些手势幅度较小，并且一些手势信号包含了手型的变化，该数据集能够评估动作识别算法的识别准确率。视频的分辨率为320×240，视频设计了20个主题，每个主题中按照不同的顺序完成24个手势信号动作，每个主题中包含24×20个动作。选择前5个主题作为测试集，后10个主题作为训练集。

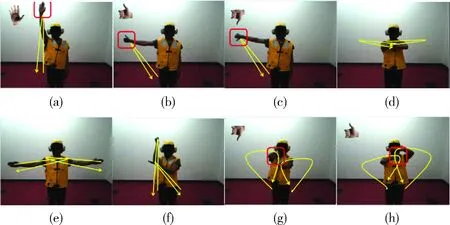
图8 NATOPS视频数据集的8个机场信号手势

4.2.2 算法的识别准确率

为了评估本算法对小幅度动作的识别性能，在提取特征之前，选择64×48个帧作为深度学习特征的时间模板，表2是4个隶属函数分别对不同维度特征的识别准确率。从表中可看出，总体而言，RGB颜色特征的准确率优于时间特征，因为对于小幅度的人体动作，动作与人体发生较多的重叠现象，在这种情况下，颜色特征的判别性更高。

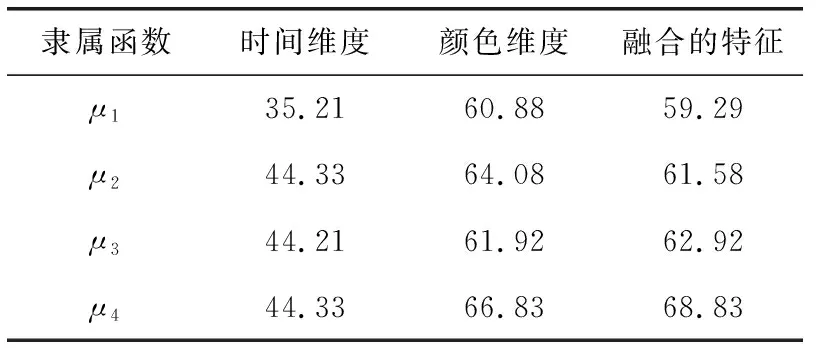
表2 4个隶属函数对不同维度特征的识别准确率/%

根据表2的结果，μ1函数的效果较差，而μ2,μ3,μ4这3个隶属函数分别强调了时域前期、中期、后期的显著性。将μ2,μ3,μ4这3个隶属函数进行叠加融合，使用融合的隶属函数重新测试对NATOPS数据集的识别准确率。将本算法与其它6个支持小幅度手势识别的动作识别算法进行对比，分别为文献[19,20]中实验的5个算法，见表3。从结果可看出，本算法融合了运动信息与RGB三色特征，对小幅度的动作表现出较高的识别准确率，明显地优于前4个算法，C_HCRF算法通过提取视频序列的多视角特征，能够有效地解析视频的多层次信息，也取得了极高的识别准确率，与本算法接近。

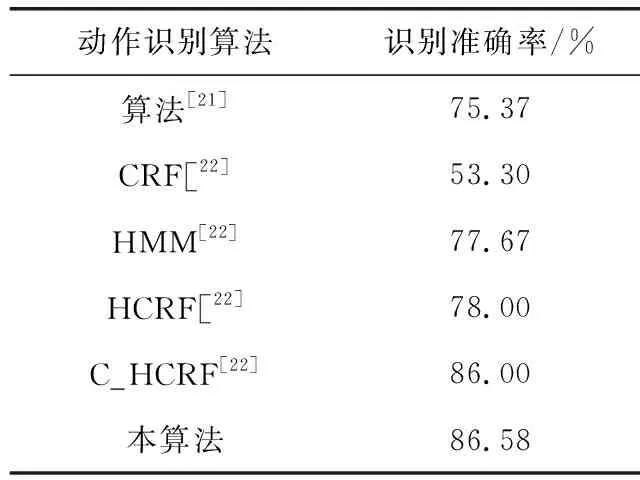
表3 6个小幅度动作识别算法的识别准确率结果

5 结束语

为了同时满足大规模数据集与小幅度动作的识别，设计了基于多特征融合与运动信息的人体动作识别算法。在双层核极限学习机的第一层，采用线性核极限学习机学习密集轨迹特征与深度学习特征，全面地表征视频序列的动作特征；在第二层，为核极限学习机训练径向基函数，将密集轨迹特征与深度学习特征进行融合。在深度学习特征中，通过时间模板分析视频序列的运动信息，为运动信息的不同时域分配不同的显著性，视频序列的时间模板输入卷积神经网络中，学习人体动作识别的特征集。该算法的手工特征与深度学习特征具有互补性，从不同的角度描述了视频的人体动作信息。基于大规模真实数据集与小幅度手势数据集进行了仿真实验，实验结果验证了本算法的有效性。