遗传算法改进的多模式污染物集成预报
邓雪晨,熊聪聪+,董 昊
(1.天津科技大学 计算机科学与信息工程学院,天津 300222; 2.天津市气象局观测与预报处,天津 300072)
0 引 言
目前大气污染物浓度预报方法主要分为统计预报和数值预报[1]。国内研究大多采用数值预报模式[2]且已经得到广泛应用[3,4],但由于各个数值模式化学参数化方案等方面存在差异,使得各个模式在预报能力上存在不同,多模式集成技术正是利用各模式中心预报的结果减少模式系统性的偏差[5],现已作为一个重要发展方向。陈焕盛等采用多元线性回归方法集成各空气质量模式预报大气污染物浓度,实验结果表明,集成预报模式优于单个预报模式[6]。秦珊珊[7]提出针对大气污染物PM2.5,建立人工智能优化神经网络模型进行预报。Zhang Ping等[8]利用当地的地理信息资源,提出用改进的BP人工神经网络进行大气污染物PM2.5浓度的预报,仿真实验得出隐含层神经元为20时精度较高。Sun等[9]通过实验验证了基于SVM的空气质量预报模型(PM2.5)能有效应用于大气污染物浓度预测,但在极端情况下预报精度有所下降。
总的来说,多模式集成预报的研究成果多采用线性回归、机器学习等方法进行预报。线性回归针对非线性问题解决能力较差,而神经网络具有很好的解决非线性问题的能力,但其中BP神经网络算法缺陷是学习速度较慢、训练过程会陷入局部最小及不能确定隐层的神经元个数问题;而遗传算法缺陷是训练时间较长,训练过程中容易出现早熟。本文采用多种单模式作为算法输入层,利用极限学习机优秀的非线性映射能力改进遗传算法迭代速度慢,容易早熟的缺点,在不断迭代过程中加快子代种群的搜索速度,达到精度高、收敛快的效果。在气象局大气污染物浓度预报数据基础上,用提出的改进算法与BP、SVM、遗传等集成方法进行对比实验,验证了改进算法的有效性。
1 多模式集成算法
1.1 遗传算法
遗传算法作为一种全局优化算法,基本原理是取n维向量x=[x1,x2,…,xn]表示成由xi(i=1,2,…,n)所组成的符号串,符号串中每一个xi看作成一个遗传基因,则x作为由n个遗传基因所组成的染色体链,多个染色体构成的种群叫作初始种群。将假设的染色体置于问题中,首先设定目标函数对每个个体进行评价,给出适应度以评判染色体的优劣程度。按照适者生存的原则,选出适应度较高的个体进行复制、交叉以及变异,产生适应度更好的新一代种群,个体x适应度越大,越趋近于最优解。随后,根据适应度选取一定的个体作为下一代种群继续进化,如此进行多次后,算法收敛于最好的染色体(最优或次优解)。
遗传算法存在过早收敛、计算时间长等问题。所以针对遗传算法的改进国内也有很多研究成果。曲志坚等[10]通过自适应方法改进遗传算法,有效地把握总体的进化方向,提高全局收敛能力。陈璐璐等[11]将遗传算法与粒子群算法相混合,用粒子群方法优化速度和位置,从而提高运算速度和精度。
1.2 极限学习机
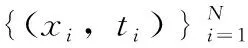
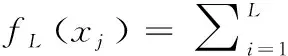
(1)
式中:a=[ai1,ai2,…,ain]即为输入层与隐藏层间第i个节点的连接权值;βi=[βi1,βi2,…,βin]T即为隐藏层第i个节点与输出层的连接权值;g(aixj+bi)为第i个隐层神经元的输出,g(·)为神经元激活函数。单隐层前馈神经网络模型如图1所示。
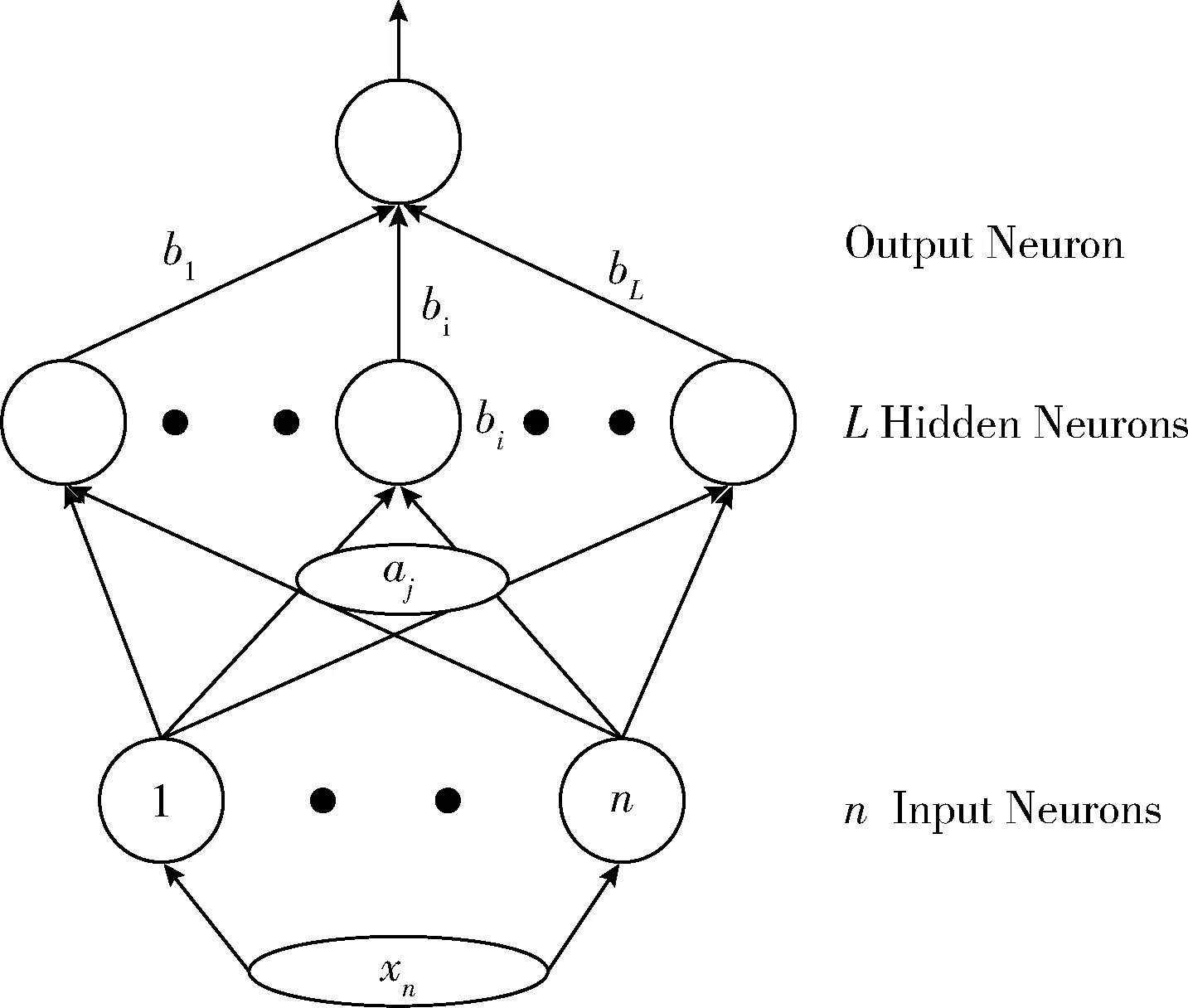
图1 单隐层前馈神经网络模型
式(1)还可以表示为
Hβ=Y
(2)
式中:H即为神经网络的隐含层输出矩阵,具体形式可以表示为
(w1,…,wL;b1,…,bL;x1,…,xn)=
单隐层前馈神经网络的隐含层神经元定义请参见文献[12]。因此,当激活函数无限可微时,隐含层与输出层的连接权值通过求解最小二乘值获得
(3)
式中:H+为矩阵H的广义逆。
2 遗传算法改进的多模式集成预报模型
构建多模式集成预报模型的目标是实现对天津本地6种大气污染物(NO2,O3,PM2.5,PM10,CO,SO2)要素进行客观精细化集成预报。资料时间长度为2015年全年每日预报数据值。
2.1 输入层对象的选择
本文采用集成多个单一预报模式的方法,针对春(3月-5月)夏(6月-8月)秋(9月-11月)冬(12月-2月)4个季节分别进行单模式的选取。所用方法在满足显著性检验基础上,针对每个季节的8种不同模式以及实况值通过数学公式计算出相对偏差(standard deviation,SD)和相关系数R进行筛选。在此基础上,将选出的单模式进行主成分分析,选取贡献率在95%以上的各主成分并判断各单模式在多个主成分的分析中是否占有一定比重。如式(4)、式(5)所示
(4)
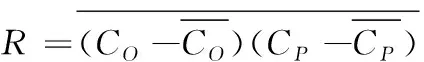
(5)
其中,σo、σp分别表示实况值和模拟值的标准差,CP为模拟值,CO为实况值。
春季或冬季筛选出7种单模式或方案:BREMPS、MADE、MOS、MYJ、MYN3、BL、YSU;夏季4种单模式或方案:MOS、MYJ、MYN3、YSU;秋季8种均符合。采用集成预报的目的不仅在形式上要比单模式预报简洁,并且还要具备更好的稳定性和精准度。
为了更好地体现各单模式的客观预报能力,集成过程并不是简单地平均分配权重,平均分配权重效果并不理想,而是针对单模式的能力给出合理权重,并且权重的分配具体到每个成员在不同时间点的区别。集成预报式(6)如下
(6)
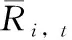
2.2 集成预报算法
模式预报会随季节变化呈现一定规律,过多选取样本会造成计算量大且描述预报规律不准确,导致过拟合。最佳方案是在分季节预报基础上找到预报时刻最近30 d的历史数据作为训练样本,即待集成数据所对应训练样本均为滚动更新,每个样本的实况值为网络训练的输出,所以输出层神经元为1。注意模型训练之前要对数据进行归一化处理。
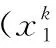
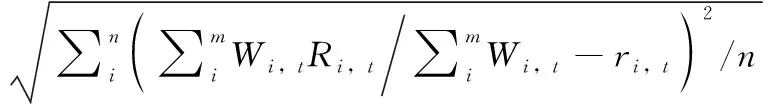
(7)
式中:i为集成预报成员模式;t为预报时间点;m为成员个数;n为一次预报时间点数目;E为集成结果与实际数据的均方误差;Wi,t为第i个成员模式在第t个时间点上的权重系数;Ri,t为该污染物第i个成员模式在第t个时间点的预报值;ri,t为第i个模式在预报时间点t的实况值,计算使得污染物集成预报均方误差的倒数达到最大。ELM进化机制公式如下
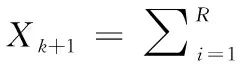
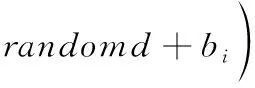
(8)
式中:Wi=[Wi1,Wi2,…,Win]T∈Rn为初始随机输入权值,bi=[bi1,bi2,…,bin]T∈Rn为初始随机输入偏置值。
训练样本的构建是引入遗传算子的ELM进化机制的关键,这里采取遗传算法对初始种群进行进化,生成的第evolution代子种群和父种群作为训练样本,其中父代作为ELM进化机制的输入,而子代作为输出。引入的种群进化代数evolution,映射出父代种群和子代种群的复杂非线性关系,获得更好搜索方向的ELM进化机制。evolution的选择针对种群进化速度至关重要,选取evolution代数太多,训练后的ELM进化机制时效性变差;选取evolution代数太少,进化速度变慢。为此,evolution的选择通过实验仿真选取,且选取多代父种群和子种群以扩大训练样本,避免初始阶段进化不显著的缺点。算法的整体改进克服了传统遗传算法中凭经验确定算子参数的问题,使获得下一代子种群的机制上更加成熟。步骤如下:首先,将训练样本集归一化处理,将输入、输出的单模式权重组成的染色体种群样本限制在[0,1]区间中,随机给定初始权重和偏置,指定种群进化代数evolution和隐藏节点数N;然后,通过改进的ELM算法求出网络输出权值βi,获得ELM进化机制。输入层到隐含层的激活函数采取sigmoid函数
(9)
算法第二部分采取ELM结合改进遗传算法模型,首先随机生成单模式权重并用实数编码组成染色体,形成初始种群。随后,第一代种群由遗传算法生成,子种群一部分由遗传算法生成下一代种群;另一部分由已经训练好的ELM进化机制来生成下一代种群,从而得到更优的搜索方向和搜索范围。两种机制根据计算得到的种群适应度adapt的优劣来判断下一代子种群的分配比例,具体步骤如下:
(1)初始化种群规模M、隐藏节点n等变量。
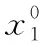
(3)根据第一代初始种群,设定初始分配比例p=0.5。
(4)依据分配比例p,将遗传算法的子种群进行选择、交叉、变异算子操作生成下一代种群。
(5)依据种群进化代数及种群扩大数训练ELM进化机制,根据比例p获得部分子种群代入ELM训练机制进行训练。
(6)分别计算两种算法的适应度adapt1,adapt2,将下代子种群分配比例进行调整
(10)
(7)计算迭代误差ek,若ek
(8)达到最优,输出结果。
2.3 实验结果与分析
2.3.1 参数选择
本文筛选了8种模式中符合要求的模式,预报结果采用均方根误差、绝对误差等指标,对单模式及多模式集成预报进行效果评估。算法参数见表1。
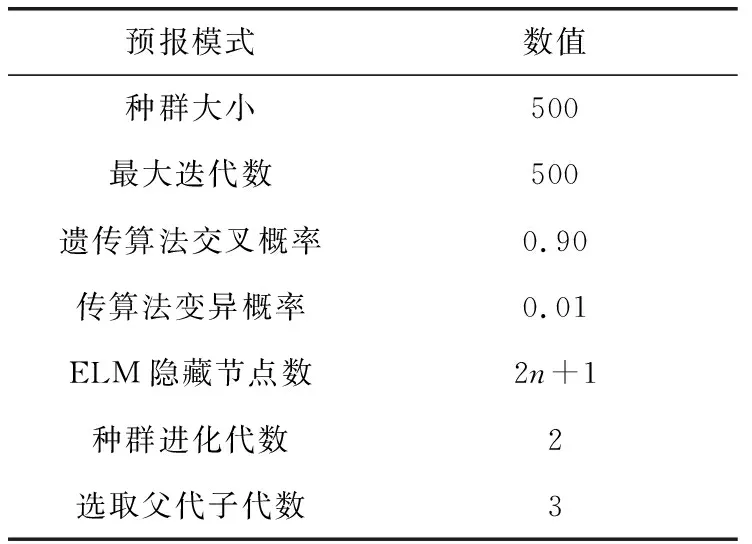
表1 算法参数
2.3.2 数据处理
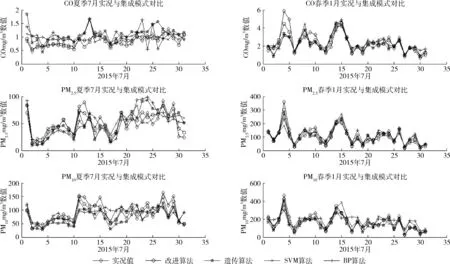
模式的选取采用各模式与实况值的显著性分析检验,显示P-value大于0.01,小于0.05,表示差异显著;P-value小于0.01,差异极显著。针对显著的模式方案进行相关性R以及偏差T分析,相关性R采用统一标准:取绝对值后0 0.5为低度相关,0.5 如表2所示,在显著性检验低于0.05的显著性差异基础上,针对各季节进行偏差及相关性分析,冬季相关性和偏差较高,选取相关性0.8以上且偏差在同范围的相关模式CUACE、MADE、MOS、YSU、MYJ、BL。 表2 CO冬季单模式方案筛选 2.3.3 ELM改进遗传算法多模式污染物预报模型检验 图2给出了全年天津站点6种大气污染物均方根误差的3种典型单模式以及SVM算法、BP算法、遗传算法与改进算法的预报结果对比,按照春夏秋冬4个季节进行预报。 图2 大气污染物集成预报模式及单模式的均方根误差比较 由图2可见,相较于3种单模式,4种集成模式均展现出了较好的均方根误差能力,而引入遗传算子的ELM改进遗传算法模式又比其它3种集成模式更优秀。改进算法的一氧化碳均方根误差降低到0.46 mg/m3,平均绝对误差值降低到0.35 mg/m3;二氧化氮均方根误差降低到12.60 mg/m3,平均绝对误差值降低到9.36 mg/m3;臭氧均方根误差降低到17.25 mg/m3,平均绝对误差值降低到11.7 mg/m3;PM2.5均方根误差降低到30.21 mg/m3,平均绝对误差值降低到23.8 mg/m3;PM10均方根误差降低到60.50 mg/m3,平均绝对误差值降低到38.9 mg/m3;SO2均方根误差降低到10.75 mg/m3,平均绝对误差值降低到7.76 mg/m3。其中冬季预报结果最优,其次是秋季、春季,预报效果最不稳定的是夏季。这与参与集成的多个模式各有优劣且夏天受温度、风力等气象因素影响较大相关,导致预报结果RMSE的增长。 图2已显示出集成模式预报效果普遍高于单模式且冬季和夏季分别是预报效果最好和最不稳定的季节,图3采用6种大气污染物的SVM算法集成模式、BP算法集成模式、遗传算法集成模式、引入遗传算子的ELM改进遗传算法集成模式与实况值的预报结果进行对比分析,选取2015年预报效果最好的冬季单月以及预报较不稳定的夏季单月。 图3 大气污染物集成预报模式与实况值的结果比较(1) 由图3、图4分析出:①在预报效果最好的冬季,4种集成方法均有良好的精度,但从细节上可以看出改进算法整体上更加贴近实况值;②预报效果最不稳定的夏季,BP算法和遗传算法因存在收敛不到最优解,整体预报不稳定的缺点,预测曲线与实况值有一定偏差。改进算法集成预报利用ELM改进搜索方向,加快收敛速度,较其它3种集成方法明显更加贴近实况值且稳定,而SVM虽然有少量预报结果比较贴近实况值,但整体上改进算法精度更好。 在算法的执行时间上,改进算法与遗传算法相比,30天滚动的分季节遗传算法在4个季节中平均用时614.98 s,引入遗传算子的ELM改进遗传算法集成预报用时281.79 s。后者的执行时间明显更快,这是因为ELM优良的非线性映射能力,通过进化代数以及父代子代种群的设置让遗传算法拥有了更好的搜索方向,扩大了进化机制的搜索范围。其中迭代总数500次中遗传算法平均收敛次数为381次,引入遗传算子的ELM改进遗传算法网络为247次。由此可见,引入遗传算子的ELM改进遗传算法比遗传算法迭代次数上的优化使其更加精确快速。引入遗传算子的ELM改进遗传算法集成方法可以满足气象预报中高时效性的要求,能在尽可能短的时间内提供准确性高的预报结果。 (1)与遗传算法集成模型相比,改进算法模型改进ELM算法输入并模拟遗传算子操作,运用改进的ELM算法与遗传算法相结合,具有收敛速度快,不易陷入局部最小的缺点,可以较好发挥大气污染物预报作用。 (2)本文考虑了季节性影响且设置30天动态滚动数据集。结果显示,冬季预报结果最优,其次是秋季、春季,在预报精度较不稳定的夏天,本文算法也展现了较其它算法更好的预报精度和整体稳定度。 (3)今后研究方向为:①改进算法中选取的父代子代参数变量通过仿真实验得出,尚未得到理论证明,需要更深入的研究;②集成预报模型的建立受到数据集数量和质量等的影响,后续还需大量数据进行实践。 图4 大气污染物集成预报模式与实况值的结果比较(2)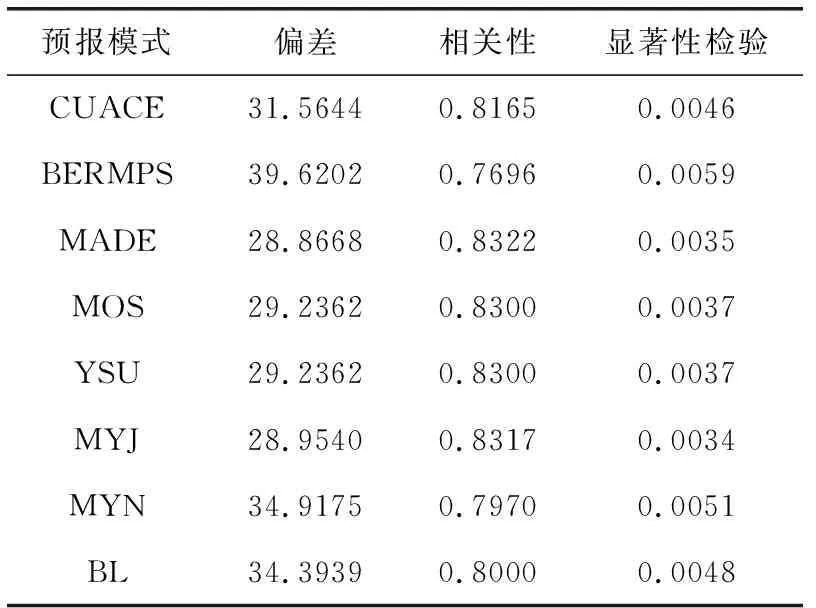
3 结束语