基于信誉值的结构化数据访问控制模型

许浩海，于 炯,+，卞 琛，鲁 亮，金 亮

(1.新疆大学 软件学院，新疆 乌鲁木齐 830008； 2.新疆大学 信息科学与工程学院，新疆 乌鲁木齐 830046)

0 引 言

随着互联网系统分布式开放系统的发展，传统的访问控制[1]模型也暴露出了许多问题，例如自主访问控制中的权限传递问题和强制访问控制中的逆向访问信道难以去除的问题等，这些模型的局限性使得迫切需要寻找新的访问控制策略解决方案，以达到动态授权的需求[2]。基于角色的访问控制在20世纪90年代迅速发展，形成的RBAC模型也成为了ANSI标准，角色是一组权限的集合，虽然RBAC模型获得了广泛的认可，但是其难以实现个体的差异性，无法满足分布式系统发展的需求[3]。近年来，出现了基于可信度计算的访问模型[4]，可以在改进RBAC模型的基础上实现个体的差异访问控制，建立信誉体系，其中最重要的衡量标准就是信誉值，信誉值的准确度决定了个性化访问控制需求的符合度。

1 相关研究

在分布式系统安全中，访问控制技术可以在一定层面上保证系统主体的合法接入，确保不同角色的资源信息互不干扰；同时，系统中数据保护也越来越受人重视，人们也在不断研究数据隐私保护，对如何在访问控制过程中合理访问隐私数据进行了深入探讨。访问控制是通过某种途径显式地准许或限制主体对客体访问能力及范围的一种方法，其核心机制是授权策略。从传统的访问控制技术延伸出基于角色访问的静态访问控制和基于任务和工作流的动态访问控制等[5]。雷蕾等[6]在加密的基础上通过访问控制策略隐藏机制生成密钥推导图来分发密钥，提高了密钥获取的计算速度。高训兵等[7]在属性加密算法基础上引入代理服务器，建立权限分析方案，实现访问权限的传递。刘庆云等[8]在量化用户和服务的基础上提出一种灵活粒度的访问控制机制，既能支持权限动态调整又能支持条件角色迁移，另外该机制还提高了访问控制的可管理性。张伊璇等[9]利用博弈论原理建立隐私访问者和保护者之间的博弈模型，该模型从收益的角度出发再结合历史信息分析隐私访问者和保护者之间的博弈策略所对应的收益继而起到阻止隐私保护者不希望访问者访问隐私的作用。Chebotko A等[10]针对云环境的特点，在云计算中通过改进的RBAC模型实现访问控制的优化。Sabrina D等[11]针对特定用户访问的数据进行选择性的加密来提高效率，保护数据安全。

从整体来看，访问控制领域的研究较为成熟，但是针对不同的应用背景，设计出特定约束的解决方案成为了新的热点，例如文献[12,13]，针对特定数据进行加密处理来达到安全访问控制的目的。本文针对扩展的RBAC模型，基于用户可信度访问控制模型上，在可信度的计算上进行进一步的加强，从系统的整体出发，在系统不断运行中智能化达应变，满足初步开放式的要求，针对系统每一项访问内容设置访问门槛，根据访问者的可信度来决定是否授予访问权限。同时实现了相同角色的用户，可以拥有不同的组权限。

2 UCBAC算法详述

总体上说，UCBAC(基于用户信誉值的访问控制)大致可分为以下4个模型：基本信誉值计算模型、关联信誉值统计模型、信誉值累积模型、信誉值惩罚模型。

属性：对主体某一特征的描述，所有的属性集合构成了主体，例如：编号、姓名、头像、住址，电话等。

属性私密度：表示了该属性对主体的私密程度，对于个性化的隐私来说，不同主体的相同属性也存在不同程度的私密度，主体可以根据属性对自身的影响程度来定义不同级别的属性私密度。私密度越高，意味着发生恶意泄露造成的影响就越大。

系统的核心思想是通过把结构化数据根据属性私密度进行等级划分，各个等级设定最低信誉值访问标准，然后针对系统中的每个主体进行信誉值的计算，进而判断是否可以访问相应的数据。

2.1 基本信誉值计算模型

用户访问系统时会携带环境信息(包括IP地址、MAC地址、访问来源、用户系统类型等)，同时在进入系统时会提供用户身份信息(包括登陆令牌、证书、密钥等)。系统安全模块根据制定的系统安全策略或规则，根据每项信息的重要程度来制定每项的权重w和基本分值SC，那么基本信誉值就是根据权重累加的基本分值总和，如式(1)所示

(1)

其中，m表示项信息。

2.2 关联信誉值统计模型

关联信誉值是通过侧面衡量该用户的信誉值，系统中的主体既是数据访问者，同时也是数据提供者，在交互过程中形成相互的信誉值，信誉值不具有传递性，但是通过听取其它主体意见，从侧面调整信誉值，使得信誉值更加符合实际情况。例如，在某一系统环境下，访问者主体A访问数据提供者主体B提供的数据，主体B需要评估主体A的关联信誉值，那么主体B就需要获取从其它主体Ei对主体A的信誉值ECi。这里还要评估主体B对其它主体E提供的信誉值。这里不使用主体B对主体Ei的信誉值作为权重依据，因为如果主体存在Ei对A有较高的信誉值，主体B对Ei也存在较高的信誉值，那么主体B对A的信誉值也会比较高，如此循环，主体A在整个系统的信誉值会被迅速拉高，事实上，有可能A只是在这个局部信誉值较高，而在整个系统中的整体信誉值较低，这显然不是我们想看到的情况。所以可以根据PageRank算法的思想，我们可以得出每个主体的整体排名，以排名作为权重依据，通过PageRank算法的思想来计算关联信誉值。

幂法计算PageRank值，其算法如下：

输入：系统信誉值图G，阻尼系数a，两次迭代距离不大于Δd，表示收敛。

输出：系统中所有主体的PageRank向量。

(1)n; /*主体数量*/

(2)Et; /* n 维的全1行矩阵*/

(3)Q0←random(n);

/*初始化随机生成每个主体的

PageRank值向量*/

(4)P←G; /*通过信誉值图得出的概率转移矩阵*/

(5)S=a*P+((1-a)*/n)*Et;

/*初始的PageRank矩阵*/

(6)i=0;

(7)whiledistance(Qi,Qi-1)>Δddo

(8)i++;

(9)Qi=S*Qi-1;

(10)end wile;

(11)returnQi;

算法中(1)～(2)行为初始化数据，第(3)行随机给每个主体生成初始的PageRank值，并组成矩阵，第(4)行为通过系统的信誉值连接图统计出的连接概率矩阵的转置矩阵，也就是概率转移矩阵，第(5)行计算初始的PageRank矩阵，第(6)～(10)迭代计算PageRank值向量，直到两次相邻迭代距离小于Δd，表示已经收敛，第(11)行结束返回最后收敛的PageRank向量值。

根据PageRank值的占比进行累加每个关联的主体的信誉值得到当前主体的关联信誉值。

2.3 信誉值累积模型

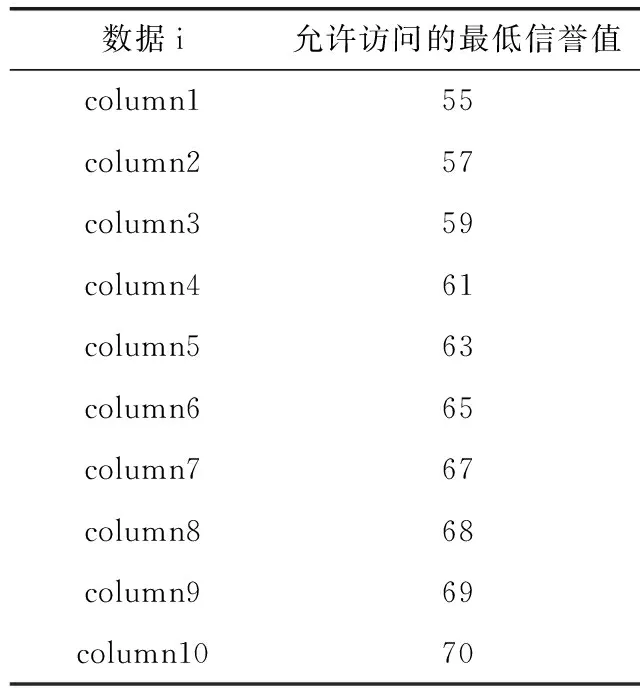
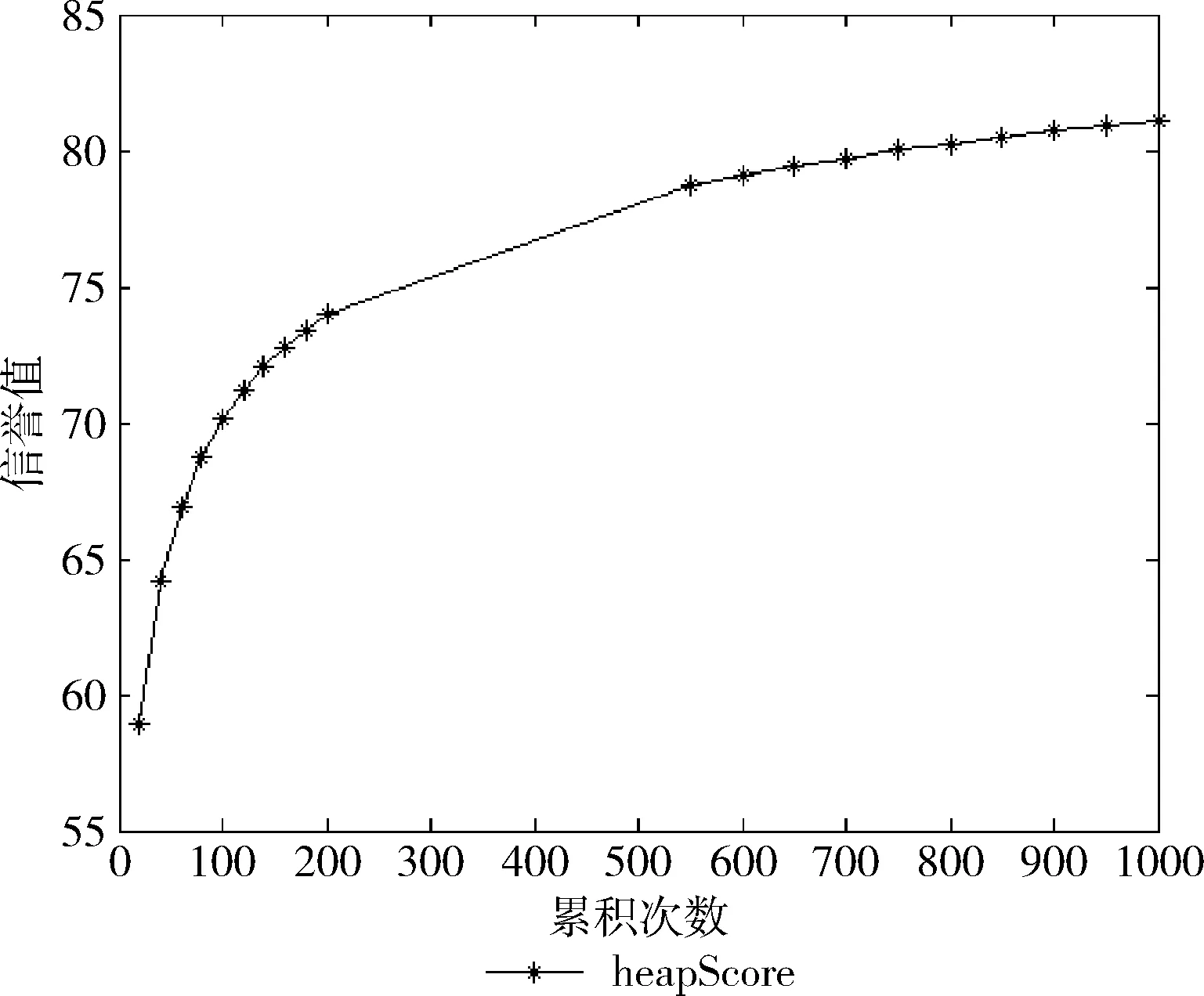
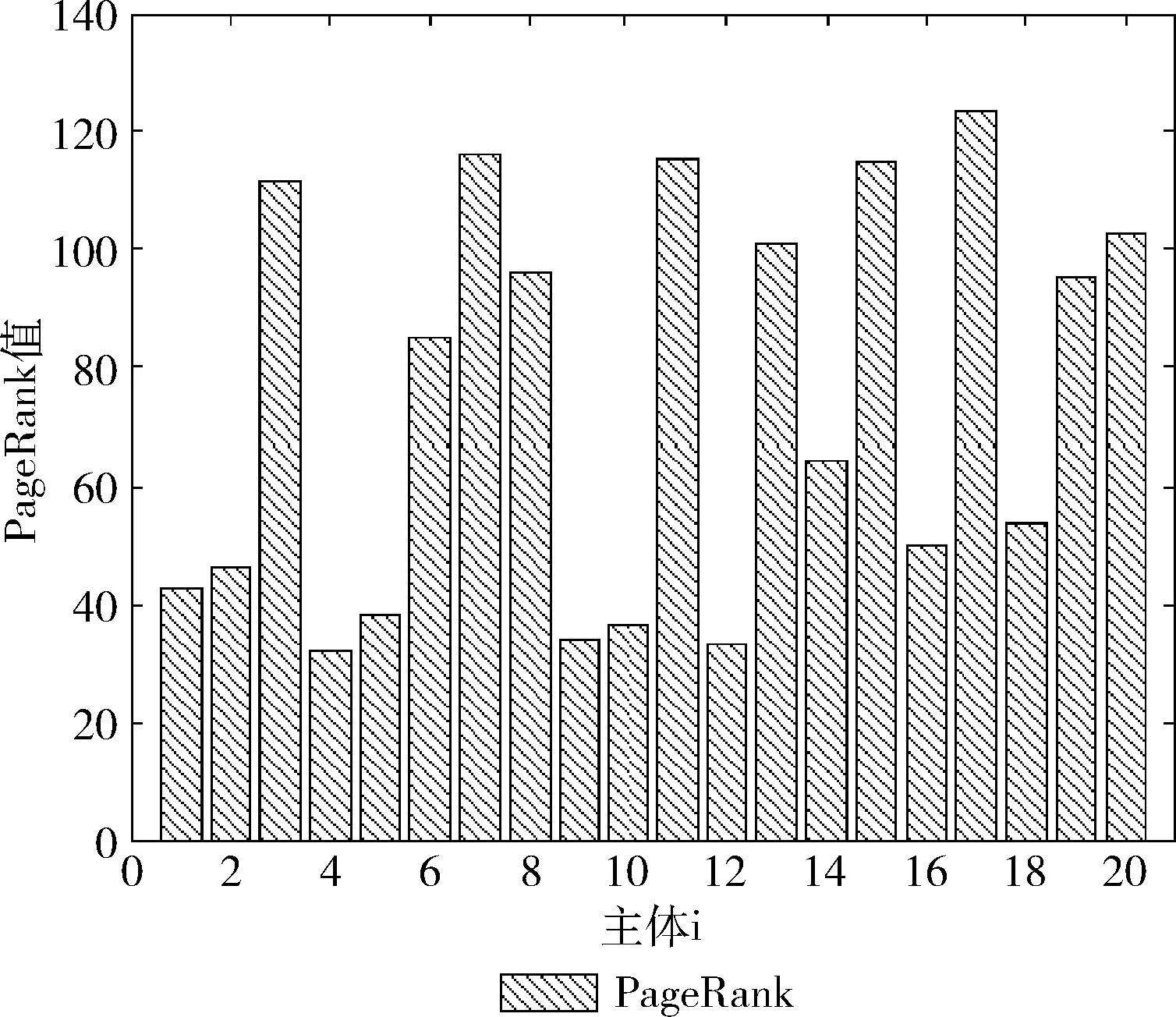
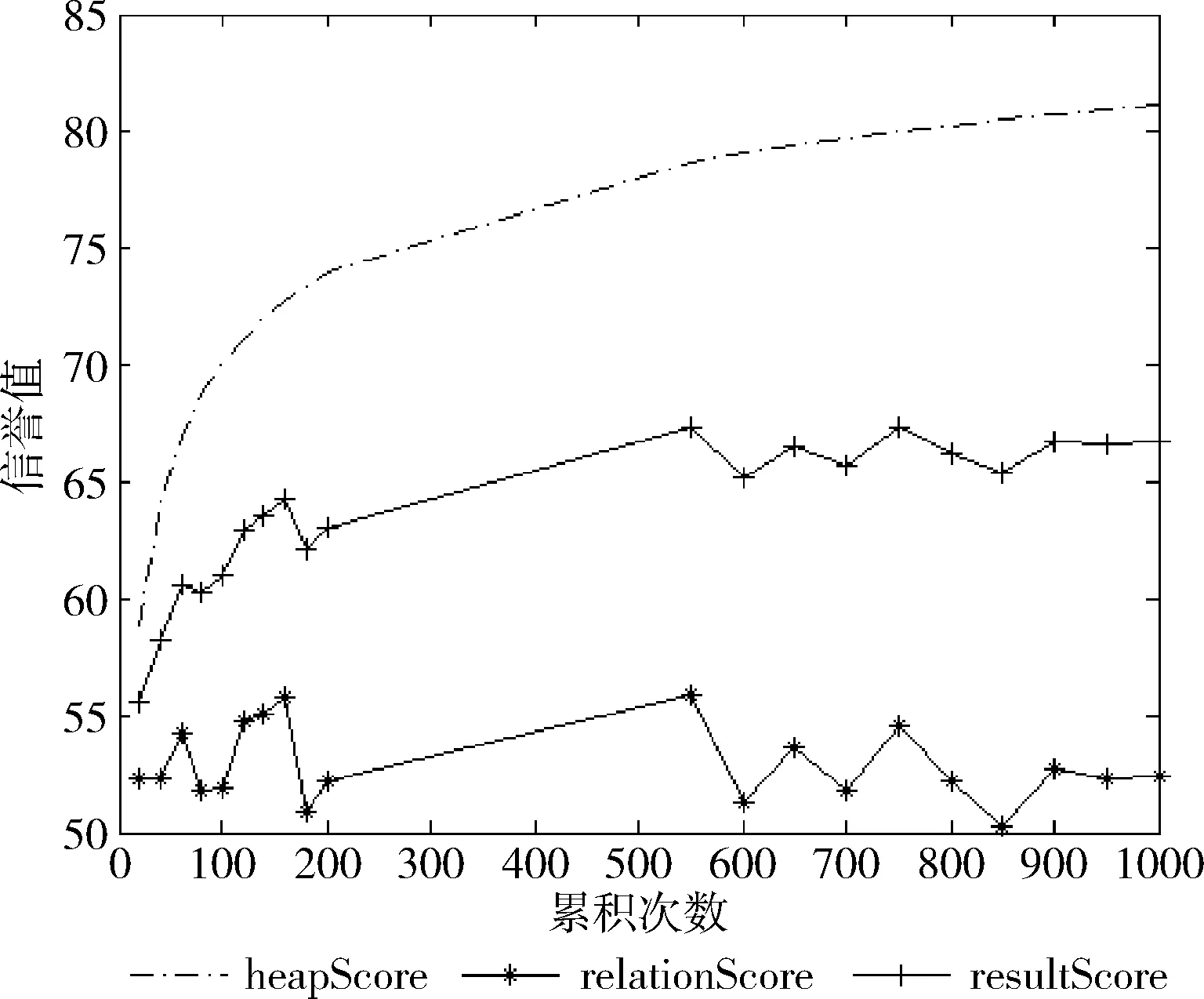
信誉值的累积必然是一个慢增长的过程，但是前期会有一个较快的增长，然后增长速度一直递减，达到一个平缓的信誉值，那么，增长的度必然是跟现有历史信誉值呈反比，最后增加一个调节参数a(其中0

(2)

很明显，式(2)的趋近值是fmax，这是一个直观的理论公式，由式(2)可以得出计算公式，那么第x次的信誉值计算公式

(3)

其中，x表示第x次累积过程，a为调节参数，调节增长的速度，增加值会随着次数增加而减少，可根据第一次的增加值设置增加速度，a的取值范围为0

2.4 信誉值惩罚模型

系统中用户的每一次数据访问记录都算作一次系统行为，根据系统制定规则和反馈将系统行为分为正向行为和负向行为，符合系统规则，数据使用的反馈良好即为正向行为，反之则为负向行为。数据私密度是对数据的重要程度的量化指标，对于违反系统安全规则的数据访问请求，并利用数据产生的负向系统行为就意味着数据的泄露，根据数据私密度计算数据泄露程度

(4)

其中，N=[1,2,3,…,n]表示数据主体的属性序号，Si为第i个属性数据的私密度，当i的取值从1到n时，数据私密度G等于1，表示该主体的全量属性数据的私密度，意味着所有属性数据可能造成泄露，这时候信誉值直接减少到0。

惩罚过程对n调整到以前的状态，也就是根据泄露程度对参与累积计算的次数进行调整，使得信誉值回到以前的指定水平

(5)

根据新的次数对累积信誉值重新进行调整，计算新的信誉值

SCnew=f(g(n))

(6)

3 实验评估与分析

信誉值累积模型中a的取值影响信誉值的累积速度，不同a值的累积信誉值趋势如下：

根据图1可以看出整体的信誉值累积速度呈现递减趋势，同时a值越小，累积速度越慢，所以实际中可以根据不同需求设定合适的a值，a值的选定可以依据大致一定信誉值的累积次数来确定。

图1 不同a值对累积速度的影响

以下面表1中数据访问所需信誉值来比较。

表1 数据与信誉值访问对照

实验中以20个主体进行测试，系统中主体i对主体j一次有效地访问表示主休i对主体j有指向，主体的关系如图2所示。

图2 主体间访问记录

在实验过程中，初始化a=0.2，初始信誉值f1=30，最大信誉值fmax=100，图3是20个主体对应累积信誉值。

图3 累积信誉值分布

图3显示了基本信誉值的累积过程，主体在每个累积次数对应的基本信誉值。

图4 PageRank值分布

PageRank值分布，如图4所示。通过计算每个主体的PageRank值，以PageRank值所占比计算得到的关联信誉值，最后计算最终的信誉值结果。

最终的信誉值是基本信誉值、累积信誉值、关联信誉值按一定占比得到的最终结果，图5中可以看出主体15的PageRank值较低，最终的信誉值有一个明显的减少，这也符合了此模型信誉值的计算，那么最终主体15可以访问的数据也会减少。

图5 累积信誉值、关联信誉值、最终信誉值分布

4 结束语

在基于信誉值的细粒度访问控制中，信誉值的评估越全面越能达到系统的要求。UCBAC从系统的几个重要层面计算信誉值，并通过对数据划分等级来判断主体可访问的数据的方式来进行访问控制。而且，针对隐私程度划分的数据也可以在用户隐私保护方面，为访问者提供合适隐私性的数据来达到数据开放性的要求。

在未来的研究中，结合数据发布要求，面向不同权限主体对系统重要数据进行不同程度的保护处理措施，比如不同程度的匿名化处理，满足系统对开放式的要求。针对安全系统中，如何对重要隐私数据进行有效的保护，防止数据在系统内部泄露导致的数据安全问题也是研究的重点。