基于Spark的投影树频繁项集挖掘算法

冯兴杰，潘 轩

(1.中国民航大学 计算机科学与技术学院，天津 300300； 2.中国民航大学 信息网络中心，天津 300300)

0 引 言

随着互联网技术的飞速发展和大数据信息化时代的来临，数据挖掘[1]已经演变为一种集大数据量与大计算量于一体的批量式处理过程。而且为了产生有效的数据信息，大部分关联规则挖掘算法需要多次使用原始数据集对候选项集进行筛选处理，使得算法效率低下。然而大数据平台这一新技术能够处理大数据的关联规则挖掘所遇到的诸多问题，它能够实现集群内部资源共享、操作的透明性高、较高的可靠性、以及一定的灵活性等特点，可以高效地处理大规模数据。

以Hadoop环境为基础，使用HDFS为底层存储工具的Spark云计算平台是近年来最为常用的大数据运算框架。频繁项集挖掘与Spark计算框架相结合有许多成功案例，Qiu H等在Spark上实现了Apriori算法的并行化并提出YAFIM算法，解决了串行算法在实现并行过程中遇到的诸多问题[3]，但该算法需重复遍历数据集，且产生频繁二项集时会出现组合爆炸问题，运算效率有待提升；Rathee S等通过构建一种新的数据存储结构，改进Apriori算法，并且在Spark上加以实现，提出了并行化的R-Apriori算法[4]，该算法仅在频繁二项集的产生过程进行改进，没有解决多次迭代原数据集的根本问题；文献[5]将FP-Growth算法与Spark相结合，得到了并行化频繁项集挖掘算法，但构建FP树产生较大消耗，算法效率仍需提高。

本文提出了一种基于Spark计算框架的投影树算法(projection tree algorithm based on Spark，PTBS)，解决了重复遍历原始数据、产生频繁二项集的组合爆炸以及并行计算时节点通信量较大等问题，提高了算法在处理大数据集时的运行效率。

1 相关技术及方法

1.1 Spark并行计算框架

Spark大数据框架因其实现了基于内存的方式储存数据，具备了快速迭代数据的能力，同时可以使用RDD(resilient distributed datasets)技术实现存储的持久化和高容错性等优势，使得它更适于处理大数据集的迭代式运算，成为大数据云计算研究者们的首选[6]。

Spark能够实现基于内存计算的基础，是其实现了一种分布式的内存抽象—RDD。RDD支持在数据集上的应用，同时也具备了数据流的特点，即：位置感知性调度、良好的伸缩性以及自动容错的能力[7]。此外，Spark还为RDD提供了丰富的内置操作，能够通过某一组操作将指定的一个RDD转化为另一个RDD，这是Spark数据处理的具体操作方式。但是，Spark实现的最主要的突破，是完成了数据的可持久化操作[8]。持久化(或缓存)一个数据集在内存中，每一个节点都会将其数据分块中的计算结果保存于节点内存，并在对数据集后续的操作中对持久化的数据进行重用。这也是Spark实现快速迭代的关键所在。

从宏观上讲，Spark的算法构造和物理执行都是以Pipeline(任务管道)为核心，基于Pipeline的思想，数据被使用时才开始计算(如Transformation算子的Lazy模式),不会产生中间结果，而在此之前，所有的操作都只是记录dataSet的转换过程。从数据流动的角度来说，是数据流动到了计算的位置。所以模式构建中要最大化Pipeline，这样既有利于并发，也利于数据的复用，会极大地提高运算效率,Spark的运行模式如图1所示。

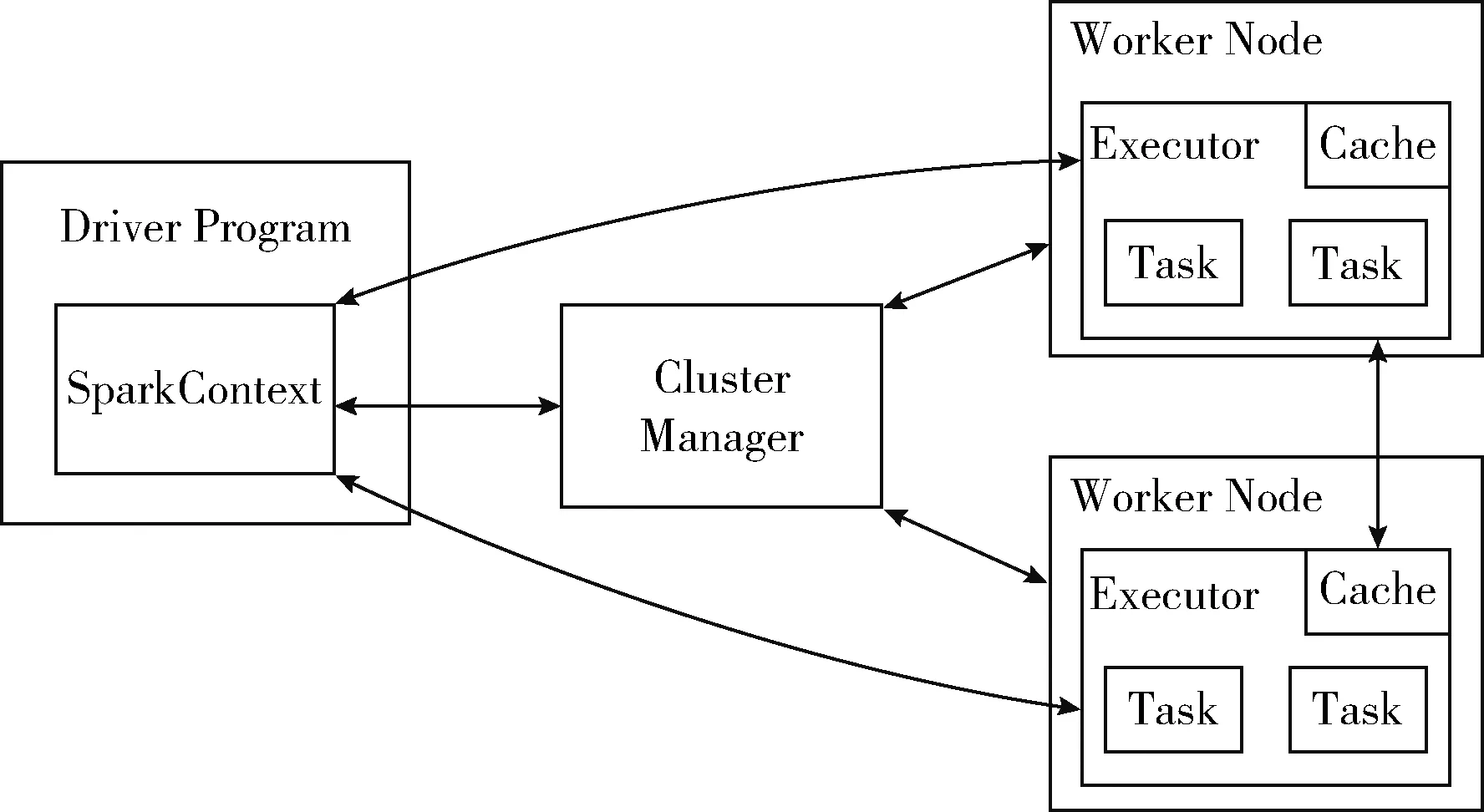
图1 Spark运行模式

1.2 广播变量

在关联规则挖掘算法实现并行化的过程中，需要在工作节点共享一些数据。为了实现这一目标，需在工作开始之前将数据广播到所有节点。Spark默认将所需的数据打包并发送到集群中从节点的每一个Task(执行任务的逻辑单元)中。然而，这将导致主节点的带宽成为运算过程的瓶颈，降低了算法的运行效率，直接限制了算法的可扩展性。与此同时，在处理海量数据的过程当中，分布式文件系统读取数据的I/O消耗也非常大[9]。为了缓解这一问题，采用Spark先进的功能--广播变量(broadcast)，它允许程序员发送一个全局只读的变量到从节点的内存中，从节点的所有Task共享该变量，而不是为每一个Task传输变量。这样可以极大地减少网络传输，节省内存空间，也隐形地提高了CPU的工作效率[10]。广播变量的作用方式如图2所示。

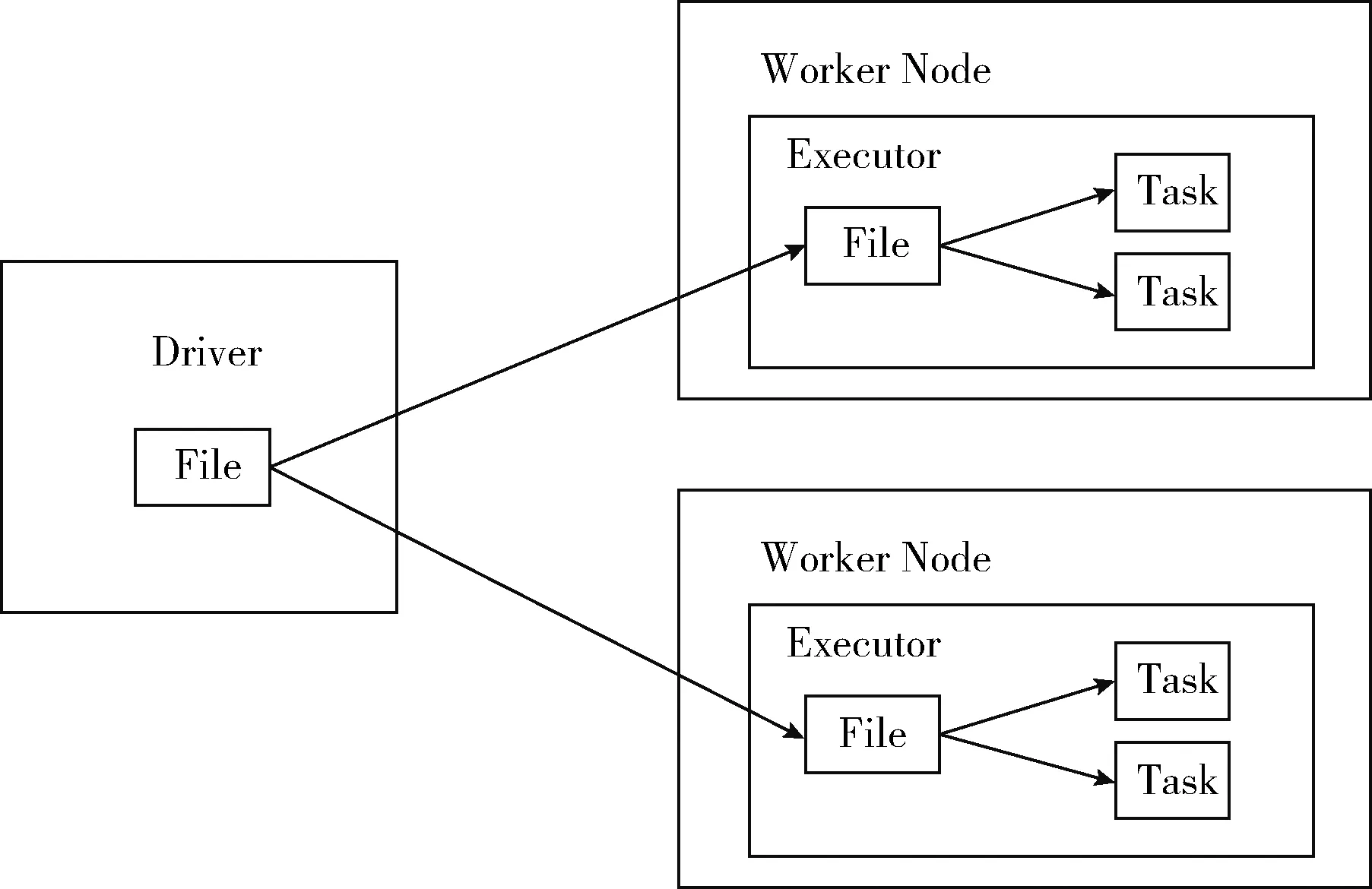
图2 广播变量工作模式

1.3 频繁项集挖掘算法

投影树算法：投影树算法利用投影树数据结构表示所有项目集，该投影树的实质是一个字典树。投影树中的每一个节点对应一个特定的项目集合，项目集的长度则对应于该节点在投影树中所处的层数。对于每一个节点，分别有一个动态项目表与之对应(因投影树以字典序排列，故动态项目表即对应节点的兄弟节点所对应项目集的最后一项)，表中每一个项目可与当前节点所对应的项目集连接，生成新的候选项集。产生候选项集的同时，会生成一个新的孩子节点代表这个候选项集。当对应于频繁项目集候选项集的节点生成时，使用数据集在投影树上投影的方式，在第(k-1)层的父节点对原事务数据集进行投影，筛选出全部数据集中与之对应的事务，并进行计数，依次来决定在算法的第k次迭代过程中所产生的候选项目集的支持度。之后以广度优先的方式对生成树进行扩展，相应于树中的每一个可扩展节点，同样保留一张动态项目表，将表中每个项目依次连接于该节点项目集，生成新的子节点项目，并用数据集进行投影、计数，筛选出新的频繁项集。

2 基于Spark的投影树频繁项集挖掘算法—PTBS

为了充分利用Spark计算框架，需要将投影树算法进行改进。首先把串行投影树算法实现并行化，改变原有数据结构，以解决重复遍历数据集带来的损耗；然后针对频繁二项集的产生进行改进，降低运算量，减少集群节点间通信的消耗；最后将Apriori先验性质添加到候选项集的筛选过程中，以减少节点间的通信量。下面，就对算法进行详细地分析。

(1)将存储于HDFS中的数据导入Spark RDD中，以便进行下一步操作。而后，使用map方法对数据进行过滤和处理，使之成为规律的，以行的形式存储的数据。其中，事务都以代表该事务的事务序号以及在事务序列中所包含的事务项组成。根据原算法思路，得出频繁项集需反复投影原始数据，为提高算法运行效率，我们在该处加以改进。

故选择对数据存储的组织结构加以改进。原始数据是将事务序列与事务项按照键值对的形式保存于RDD当中。开始，在map阶段将事务中的事务项进行分离，并分别与该事务的编号形成多个键值对，之后，在reduce阶段将具备相同事务编号的项合并。对特定事务编号所对应的序列进行统计计数，得出频繁一项集，存储结构的转换如图3所示。

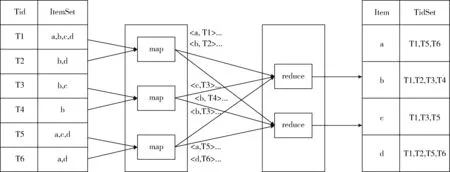
图3 数据结构转换过程

改进后实现的RDD血统如图4所示。首先，以flatMap()将数据按行读入，然后再利用flatMap()方法，将数据以Item项为单位分隔。分割完毕，用map()方法将每个Item项转换为(Item,Tid)键值对。之后再使用reduceByKey()方法将相同Item项的Tid进行连接，生成(Item,TidSet)键值对，并使用filter()把候选项集中频度小于最小支持度的项过滤，得到频度大于最小支持度的(Item,TidSet)对，而后采用map()的方式，收集对应键值对的键值，得到所有频繁一项集。此后，利用频繁一项集对原数据集进行过滤，剔除不包含频繁一项集的事务序列，算法1为获取频繁一项集所使用的算法。

算法1：获取频繁一项集

Foreach transaction t(Tid,Items) in T

flatMap(line,t)

Foreach item I in t

out(I,Tid)

End Foreach

End flatMap

End Foreach

ReduceByKey(I,Tid)

TidSet =“”

While(Item I in partition)

TidSet+=Tid

End While

If(TidSet.size>=support)

L1+=(I,TidSet)

End if

End reduceByKey

(2)按照投影树的思想，频繁二项集应当使用频繁一项集两两组合，基于第一步对数据结构的改进，可以将遍历数据集求项集出现次数改进为将两个对应的TidSet求交来产生，但因频繁二项候选集的组合爆炸以及频繁一项集对应TidSet数据量较大，会产生叠加效应，使得这一部分产生巨大的计算量。故需对该步骤进行改良。

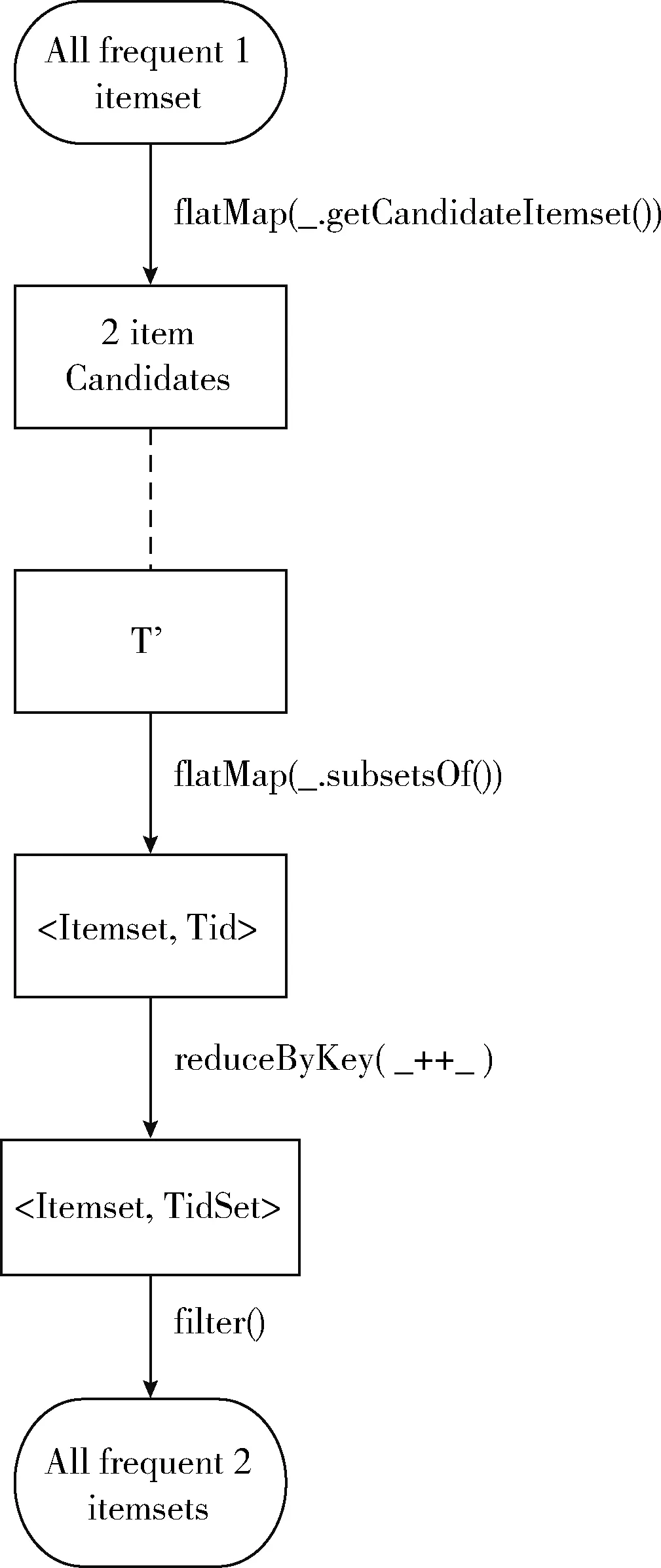
图5 第二阶段RDD血统

算法2: 频繁二项集的生成和筛选

T’=T.filter(include k1)

Read L1 from RDD

Foreach Ii in k1

Foreach Ij in k1

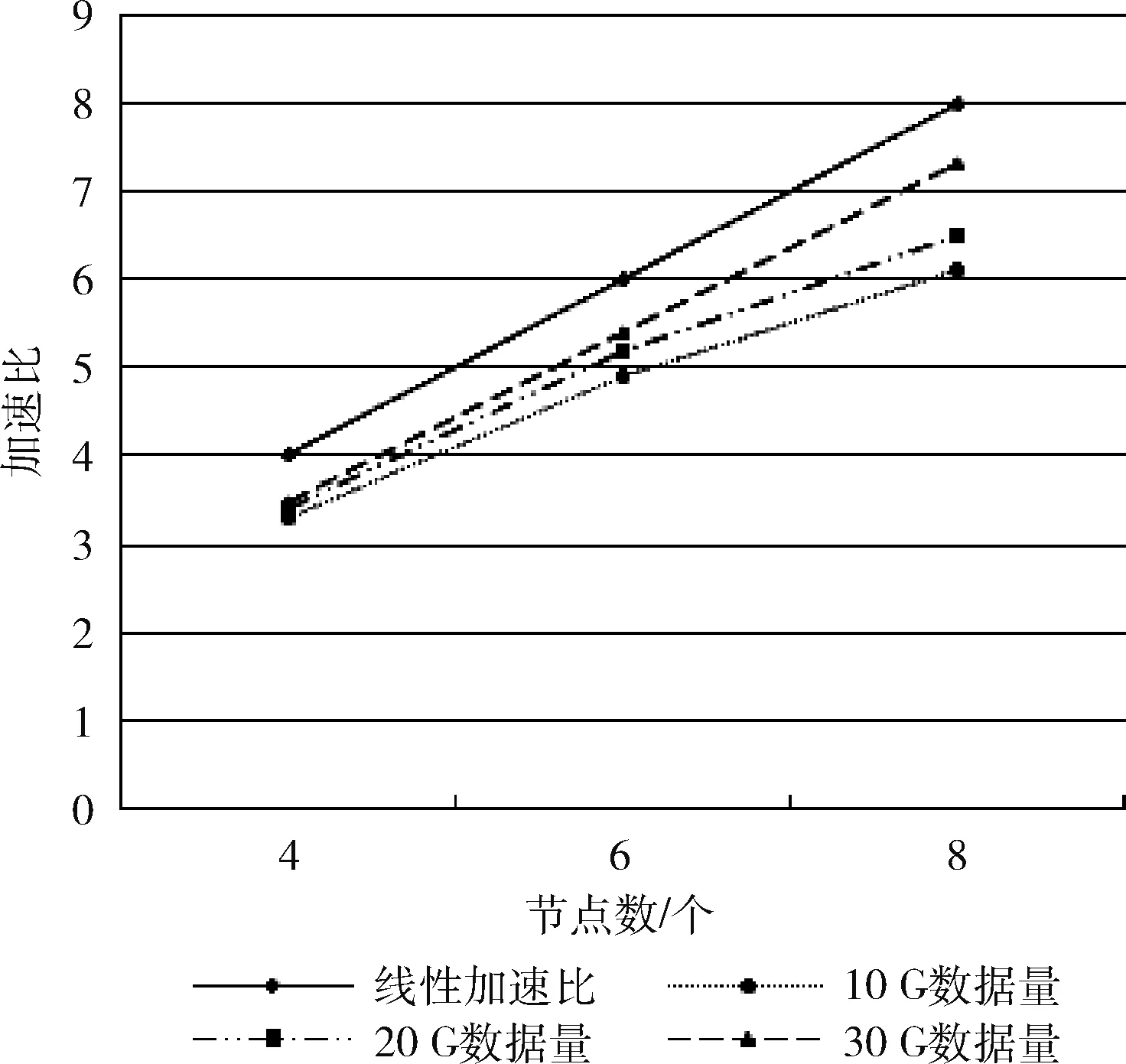
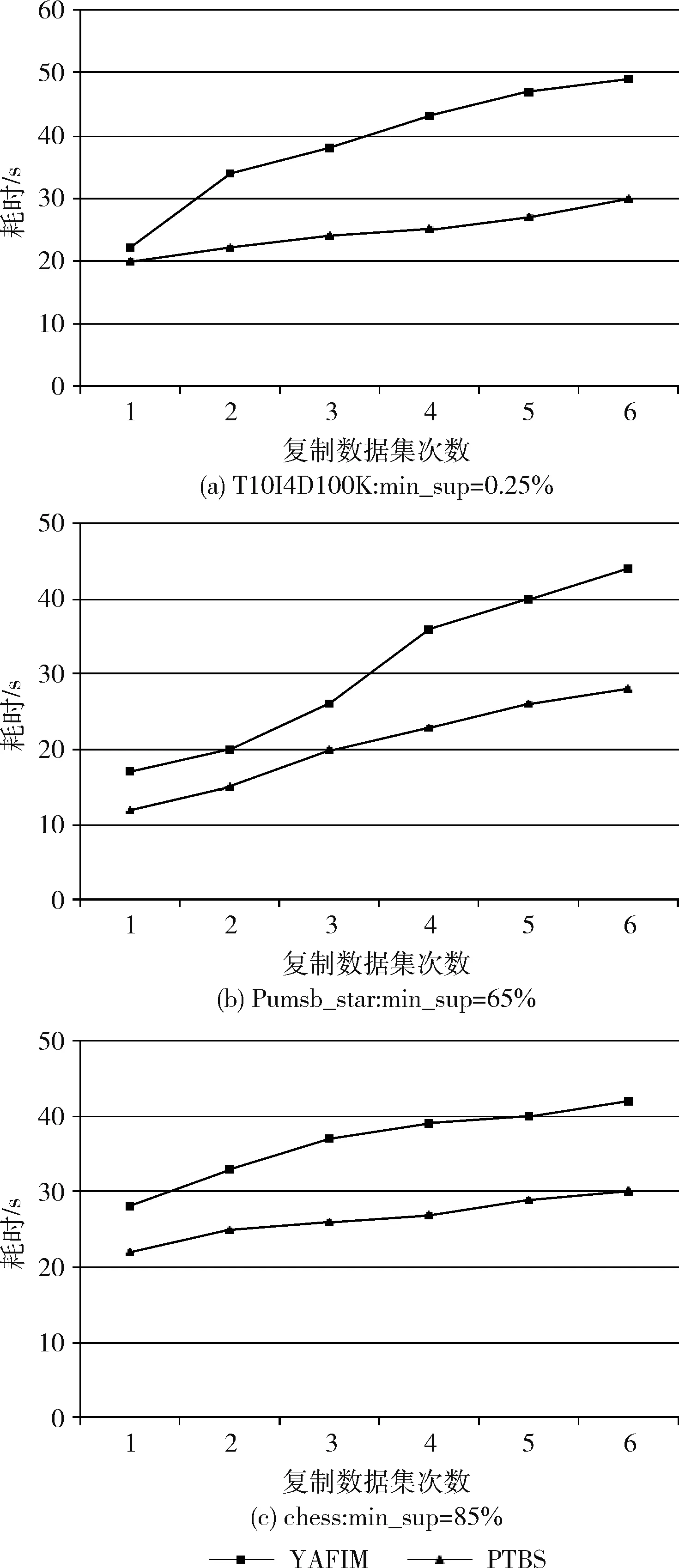
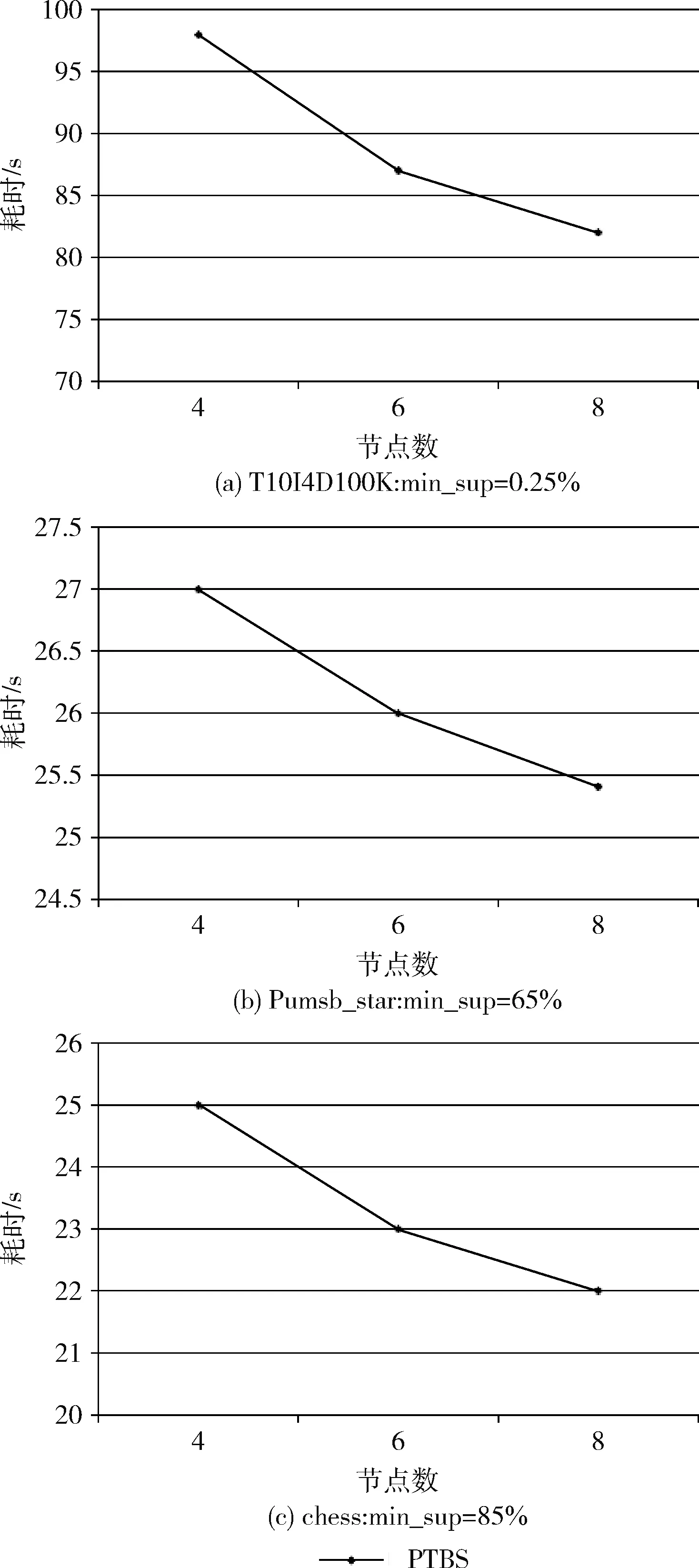
if(Ii

C2=Ii +Ij

End if

End Foreach

End Foreach

Foreach transaction t in T′

flatMap(line offeset, t)

Foreach candidate c in ct

out(c,Tid)

End Foreach

End flatMap

End foreach

reduceByKey (c , Tid)

TidSet =“”

While(Item c in partition)

TidSet+=Tid

End While

If(TidSet.size>=Support)

L2+=(c,TidSet)

End If

End reduceByKey

(3)在这一阶段，将以投影树的方式，按照宽度优先，迭代地以频繁k项集产生频繁(k+1)项集。因为投影树中所有项目均按字典序排列，故动态项目表即对应节点的兄弟节点所对应项目集的最后一项，所以在具体操作时，可利用该节点项目集依次与兄弟节点的项目集进行连接，产生子节点对应的候选项目集，即在频繁k项集集合Fk中将前(k-1)项相同的两个频繁k项集进行自连接，以模拟投影树的频繁项集连接动态项生成候选项集的过程。针对产生的候选项集，植入Apriori的先验性质加以改进，检验候选项集的所有子集是否是频繁的，这样可以极大地缩小候选项集的数量，不仅减少了集群节点间通信消耗，也减少了后续的运算量。

在算法的第二步中，数据在结构上已经被转换为键值对的形式，故在搜索频繁项集的过程当中，我们可以将支持度计数的过程改进为使用已知的自连接事务的事务序列求交集来得到包含候选项集的事务编号。得到的序列便是由包含该特定项集的事务编号所组成的，而无关事务编号将会被自动删除。在这个过程中，利用集合求交的快速运算代替遍历数据集求候选项的频数，既能节省大量时间，还可以消除遍历无关事务带来的损耗，最终得到包含候选项集的事务序列。之后对新的TidSet进行统计计数，并使用最小支持度计数进行判别，如果大于最小支持度，我们就将新生成的频繁项集和包含该项集的TidSet组成的键值对，存入F(k+1)当中。

该阶段实现流程如下，首先将满足条件的频繁k项集自连接，产生候选(k+1)项集，然后使用subsetOf()方法鉴别候选项集是否满足Apriori性质，若检验为真，则将自连接时所使用的两个项集的TidSet集合交叉计算，并利用候选项集和交叉计算得到的结果组成新的(ItemSet,TidSet)。之后，再使用filter()方法，将TidSet事务编号数小于最小支持度的项过滤，产生频繁(k+1)项集。利用这种方法，可以将遍历原数据集转换为快速的集合求交运算，并删除了无关事务，极大地提高了运算效率，算法3是第三阶段所采用算法的伪代码。

算法3：生成频繁k+1项集

Read L(k) from RDD

Foreach li in L(k)

Foreach lj in L(k)

if(li[1]==lj[1] & li[2]==lj[2] & li[3]==lj[3]……li[k]

//筛选满足自连接条件的频繁k项集

ItemSet=(li[1],li[2],li[3]…li[k-1],li[k],lj[k])

if(has_infrequent_subset(ItemSet , Lk ))

//验证是否满足Apriori性质

TidSet = li._2 ∩ lj._2

If(TidSet.size>=support)

L(k+1)+=(ItemSet,TidSet)

End If

End If

End If

End Foreach

End Foreach

3 相关实验与分析

实验室的分布式计算平台由9台计算机搭建而成，其中主节点配置为i5处理器，4 GB内存，2 TB硬盘。计算节点配置为奔腾e2140处理器，1 GB内存，500 GB硬盘,Spark集群的环境参数如下所示：

(1)Ubuntu:14.04

(2)Hadoop version:2.4.0

(3)Spark version:1.6.1

为了验证PTBS算法的正确性，使用数据集T10I4D100K、Pumsb_star和chess与同类型关联规则挖掘算法YAFIM进行比对，在得到计算结果并进行简要分析之后，发现实验结果基本是一致的。

3.1 加速比测试

为了对PTBS算法的运算效率以及扩展性加以考量，我们首先要是用自己生成的数据集对算法进行测试。在生成数据时，选择将项目数定位60，且为形成对比实验的效果，分别生成10 G、20 G、30 G大小不一的3组数据，用作进一步的实验。

加速比是指相同的任务量，使用单一处理器进行运算所使用的时间与使用多个处理器运算所使用的时间的比值。是一个被用作判断算法并行是否有效的重要标准。应用之前生成的3组人工数据分别对算法进行检验。为提高实验的可参考性，我们使用3个数据集在包含4个节点、6个节点以及8个节点的不同实验环境下进行数据处理，实验结果如图6所示。为使效果图更为明显，在折线图中加入了线性加速比结果。

图6 加速比测试

从图6可以看出，在处理相同数据集的情况下，在增加节点数之后，算法的运算效率是有明显提高的，而且运算速率的增加是趋近于线型增长的。但与标准线型增长相比较，还是有一定的差别。其原因在于：节点增加之后，各节点之间协调工作变得更加频繁，故数据的传输与节点通信数据量会大幅度增加，所以效率的增加要比理想值低。在对比不同数据量的加速比时我们发现，随着数据量的增长，加速比效率随着节点数的提高更为明显，原因在于：数据量的增长使得数据传输时间与运算时间的比值越来越大，最终趋近于无穷小。

实验数据表明，PTBS具备了一定的可扩展性。

3.2 数据的可扩展性测试

为了进一步验证算法的数据可扩展性，对PTBS算法与YAFIM算法进行了对比实验，以评估算法的运行效率。为保证实验的客观性，特使用公共测试数据集T10I4D100K、Pumsb_star和chess。其中，T10I4D100K包含100 000个事务，每个事务包含870个项；Pumsb_star包含事物数49 049，每个事务有2113个项；chess包含实物数3196，每个事务包含75个项。为了确保实验结果的精确性，图中的值为算法运行10次的平均值。

图7 数据可扩展性测试

为了检验PTBS算法的数据扩展性能，将集群的运算节点数设置为8个，使用原始数据生成实验所需要的多个数据集，分别将数据复制2、3、4、5、6倍，形成大小不一的4个数据集，再进行多次对比实验，以验证PTBS算法的扩展性。实验的数据结果以折线图的形式表示，如图7(a)、图7(b)、图7(c)所示。其中X轴表示所使用的数据集为原数据的数据量倍数，Y轴表示处理数据所花费的时间。从图7中的3个折线图可以得出结论，随着数据量的不断增加，两个算法完成任务的耗时均呈缓慢的态势逐渐增长，而PTBS算法耗时曲线的增长相对更为平缓一些。在针对T10I4D100K(最小支持度为0.25%)的实验中，相对于YAFIM运行效率的提升，PTBS的运行效率提高从开始的22%攀升到最终的32%，可见随着数据集的不断扩大，算法效率的提高愈发明显。而在数据集Pumsb_star(最小支持度为65%)的实验中，数据未复制时，YAFIM执行时间为16 s，PTBS执行时间13 s，效率提高12%。在数据不断扩增的情况下，PTBS的运算效率提高分别为15%、12%(可能由于数据集本身的属性特征提高不大)、30%、32.5%、36.4%，效率提高的百分比也在不断地增长。在最后一个关于数据集chess(最小支持度为85%)的实验中，也可以发现，PTBS运算效率与YAFIM相比，从最初的提升17.8%到最终提升28.5%，算法效率的提升会随着数据量的增加而增加。分析原因，YAFIM的每一次迭代都需要遍历整个数据集，而PTBS通过改变数据组织结构的方式，把遍历数据集计数转化为两个TidSet求交然后再计数，利用集合的求交操作代替了重复遍历数据集的过程，同时也避免了对大量无关事物的遍历，提高了运算效率,减少了节点间的网络通信量。所以，可以得到结论：相较于YAFIM而言，PTBS算法具有更高的数据可扩展性。

3.3 节点的可扩展性测试

为了检验PTBS算法的节点可扩展性，我们选用3个公共数据集T10I4D100K、Pumsb_star和chess对算法进行测试，在测试的过程中，我们还需要不断地将集群的运算节点调整为4、6、8个，以形成对照，而在此期间，实验所使用的数据集保持不变。在不同环境下记录算法处理完成数据所使用的时间，实验结果以折线图的形式表示，如图8(a)、图8(b)、图8(c)所示。其中X轴表示集群当中运算节点的个数，Y轴代表PTBS完成数据处理所消耗的时间。由多个实验图对比分析可知，在增加运算节点数之一变量后，PTBS算法处理等量数据所消耗的时间逐次递减，且递减的趋势近似于线型，结果表明，该算法具有良好的节点可扩展性。

图8 节点可扩展性测试

4 结束语

频繁项集挖掘是一门从数据集中提取知识的重要技术，针对互联网普及所带来的数据井喷式的增长，我们把原有的串行投影树算法进行了多方面的优化改进，再根据Spark云数据计算框架的技术特性加以完善并最终实现，成功地将原有算法与大数据技术相融合，实现了对海量数据关联规则挖掘技术的突破，与此同时也为后续的算法改进提供了有意义的解决算法并行化的方式，诸如如何解决重复遍历原始数据集，如何处理产生频繁二项集时因组合爆炸带来的大量的交叉计算等问题。最终使用多组对比实验，验证了我们对于算法并行化改进的操作是有效的，并且在数据量不断增大的过程当中，算法改进所带来的运算效率的提升会有更为显著的效果。