基于CS算法改进ELM的时间序列预测
赵 坤,覃锡忠+,贾振红,王哲辉,牛红梅
(1.新疆大学 信息科学与工程学院,新疆 乌鲁木齐 830000; 2.新疆移动公司监控中心,新疆 乌鲁木齐 830000)
0 引 言
近年来,神经网络凭借着好的容错率、鲁棒性以及非线性拟合的能力,使其在时间序列预[1-3]问题方面成为研究的热点之一。BP[4]、RBF[5、SVM[6]、DBN[7]以及它们的改进算法[8-11]被相继提出。但是人工神经网络存在固有的缺点:容易陷入局部最小,收敛速度慢,计算消耗时间长,网络结构不易确定等。
极端学习机[12](extreme learning machine,ELM),具有不易陷入局部最小、泛化能力好、调节参数少、训练时间短等优点。但ELM的初始权值和阈值是随机给定,隐层节点数无法确定,导致预测结果稳定性差,文献[13]中指出对于ELM的隐层节点数的确定依然是需要解决的问题。大多数学者使用组合算法来改进ELM,来弥补这个问题带来的缺陷。Yang等[14]提出一种改良的ELM算法,Geng等[15]提出一种FAPH-ELM的算法,但是都没有涉及到对ELM模型结构的改进,并且计算量大、模型复杂。还有学者选择PSO[16]、GA[17]、DE[18]等寻优算法改进ELM模型,可以智能选取合适的网络结构,有效地改善模型的性能。不过上述算法存在以下不足:①对ELM算法优化时,需要设置较多参数,耗时长;②改善模型的优化算法全局搜索能力不强;③预测结果不稳定。布谷鸟搜索算法[19](cuckoo search,CS),一种新兴启发式算法,与传统的优化算法相比,结构简单,控制参数少、寻优速度快、有较强的全局寻优能力[20,21]。本文提出一种CS-ELM算法,采用两种不同领域的时间序列数据对算法进行验证,采用单步预测和多步预测验证CS-ELM算法预测性能和效果。
1 CS-ELM 算法原理
1.1 ELM算法原理
设m、M、n分别为网络输入层、隐含层和输出层的节点数,g(x)是隐层神经元的激活函数。设有N个样本(xi,ti),其中xi=[xi1,xi2,…,xim]T∈Rm,ti=[ti1,ti2,…,tin]T∈Rm则极限学习机的网络模型可用数学表达式表示如下
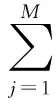
(1)
其中,i=1,2,…,N,j=1,2,…,M,式中ωj=[ω1j,ω2j,…,ωmj]、βj=[βj1,βj2,…,βjn]、bj分别表示连接网络输入层节点与第j个隐层节点的输入权值向量、连接第j个隐层节点与网络输出层节点的输出权值向量、第j个隐含层节点的偏差。把N个样本带入到式(1)中,得
T=Hβ
(2)
其中,H表示网络关于样本的隐层输出矩阵,β表示输出权值矩阵,T表示样本集的目标值矩阵
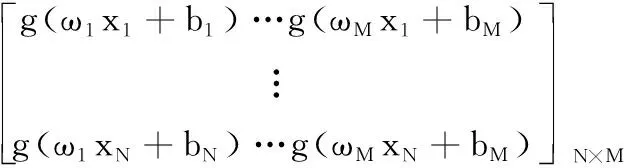
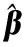
(3)
式中:H+为矩阵H的MP广义逆。
对于ELM模型,其输入权值矩阵和隐含层偏差是随机确定的,从而使得一些隐含层的节点失效或不能满足数据要求,降低了模型的预测精度和稳定性。因此,提出选择最佳的隐层节点数方法改进以上不足。
1.2 布谷鸟搜索算法原理
布谷鸟搜索算法通过模拟某些种属布谷鸟的寄生育雏过程,求解全局最优化问题。CS采用Levy飞行搜索机制,使优化算法更为有效。使用鸟巢位置代表解,该算法基于3个理想化的规则:①每个布谷鸟一次下一个蛋,堆放在一个随机选择的巢中;②最好的鸟巢将会保留到下一代;③巢的数量是固定的,布谷鸟的蛋被发现的概率为pa∈[0,1]。
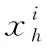
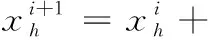
(4)
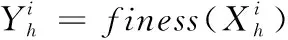
CS算法结构简单,控制参数少、有较强的全局寻优能力,并可以直接把鸟巢位置替换为最优化问题的决策变量。CS-ELM直接可以把CS算法得到的鸟巢位置作为ELM的隐层节点数,最终选择的最优鸟巢位置就是网络结构的隐层节点数。
1.3 CS优化ELM预测模型
在基本ELM模型中,隐层节点数固定后,网络结构的输入权值和隐层偏差是随机给定的,进而影响模型的稳定性。本文采用CS算法对ELM算法进行改进,自适应地选择ELM模型的隐层节点数及输入权值和阈值,流程如图1所示。在CS算法中有N个种群即鸟巢,每个鸟巢位置代表一个有理数,鸟巢位置取整后作为ELM的隐层节点数M;输入样本数据,将产生一组ELM网络的输入权值矩阵W、隐层阈值b和输入权值矩阵β,并计算样本数据预测误差作为当前鸟巢位置的适应度值。每次迭代搜索结束后,储存最优鸟巢位置和W、b、β。待满足迭代终止条件时,比较鸟巢所对应的适应度值,输出最优鸟巢位置,及其所对应的W、b、β。具体步骤如下所示。
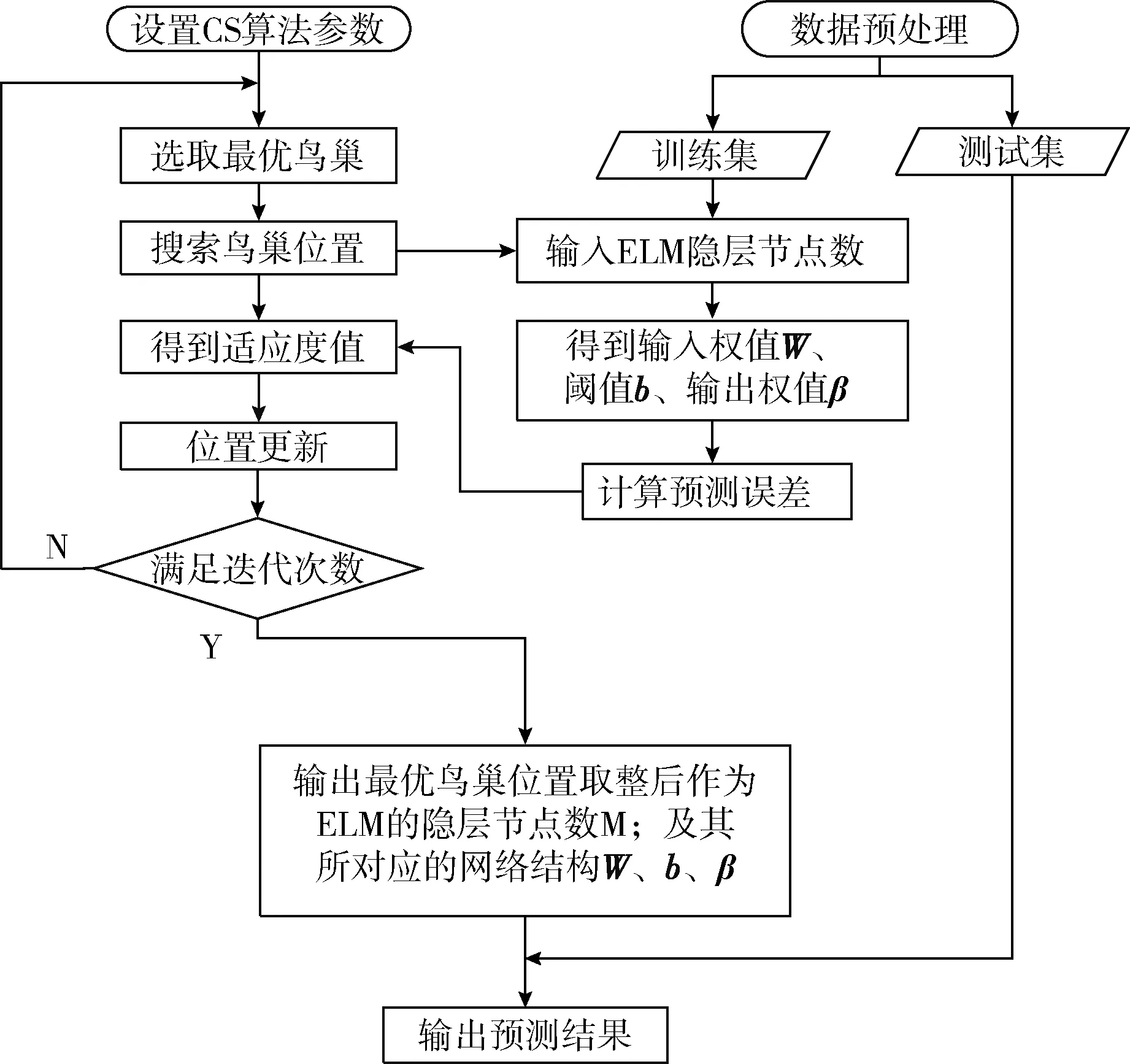
图1 CS-ELM模型流程
步骤1 数据归一化处理。
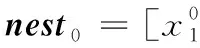
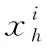
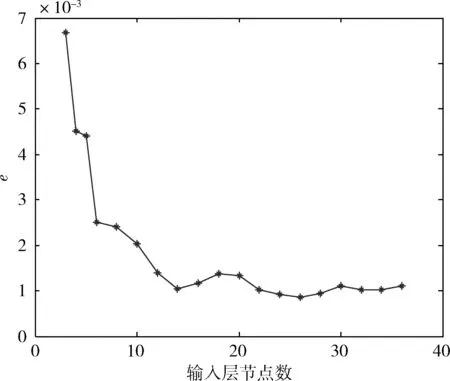
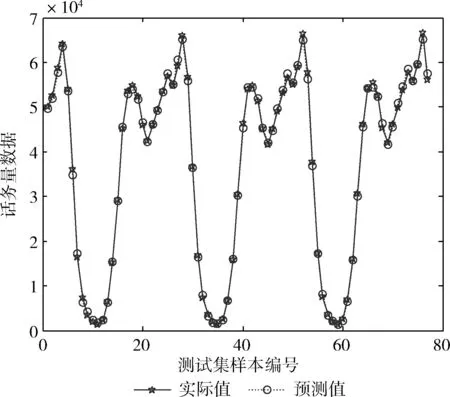
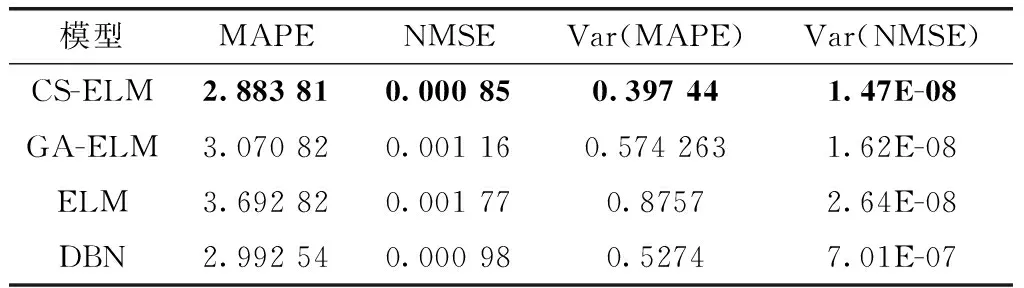
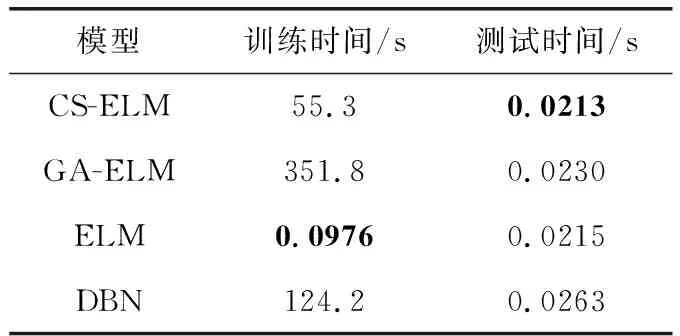
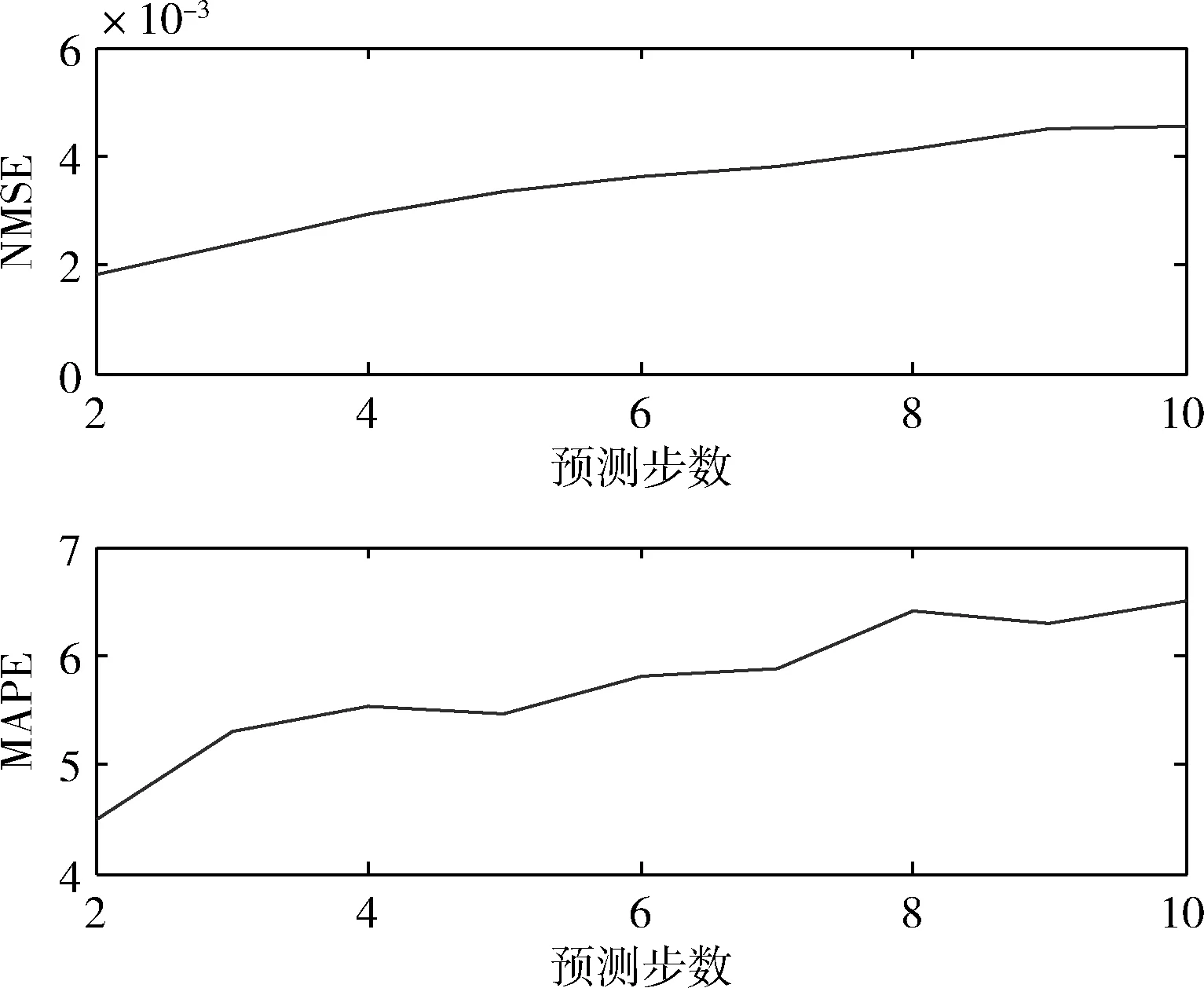
步骤4 产生随机数rand和pa比较,若rand 步骤5 若满足迭代次数,停止搜寻;否则返回步骤3。 步骤6 选取适应度值最小的那个鸟巢位置作为ELM的隐层节点数M,并输出所对应的W、b、β。建立CS-ELM时间序列预测模型。 在对时间序列数据进行预测时,为对预测性能更加客观评价预测性能,本文采用规范化均方误差NMSE(normalized mean square error)计算一次实验的规范化后的误差,采用平均绝对百分比误差MAPE(mean absolute percentage error)测量预测结果的相对误差。计算公式如下 (5) (6) 以上两种评价参数是单次实验的误差,本文将P次实验后预测误差的平均值作为最终的预测误差。但是这样不能显示多次预测中误差的波动性,即不能反映出预测模型的稳定性。因此,本文采用计算多次预测误差的方差来反应模型的稳定性,计算公式如下 (7) 2.1.1 数据准备与参数设置 对通信运营商,话务量是评价运营商经营状态的最重要的指标之一[22]。本文中的数据选取某地州某运营商的移动话务量数据,训练数据的是随机选取2012年5月19日至2012年6月20日的整个地州话务量数据,该话务量数据采样间隔是1 h。总共792个数据,选取前700个数据作为训练样本,其余的作为测试部分。 对于单步预测的CS-ELM模型,输出层节点数为1,隐层节点数由CS算法自适应的选择,故而输入层节点数的确定将影响模型的预测效果。用实验法选择输入层节点数,以规范化均方根误差eNMSE作为评判准则。如图2所示。横坐标表示输入层节点数,纵坐标表示经过50次实验后误差的平均值。由图2可知,当输入层节点m=26时,规范化均方根误差取最小值eNMSE=0.000 854。所以本次实验选取输入节点是26个。 图2 输入层节点数对预测误差的影响 2.1.2 实验结果对比与分析 采用布谷鸟搜索算法对ELM进行优化,选取一组最佳的隐层节点数、输入权值及阈值,对话务量预测如图3所示。可以看出CS-ELM的预测值和实际的话务量值几乎重合,其预测误差MAPE=2.883 81;NMSE=0.000 85。 图3 CS-ELM对话务量预测的预测值与实际值对比 采用传统的遗传算法优化ELM的模型(GA-ELM)、ELM以及DBN模型作为对比模型。在GA-ELM模型中,GA算法的种群数、搜索迭代次数等参数与本文采用的CS算法设置相同;ELM模型同样设输入节点数为m=26,隐层节点数M=120;DBN模型中输入层节点m=26,两个隐含层节点分别为L1=38、L2=57。分别做50次实验,预测误差结果取平均值,见表1。 表1 ELM与CS-ELM预测性能对比 在表1中可以看出,CS-ELM的预测误差MAPE=2.883 81、NMSE=0.000 85,而明显小于ELM和CA-ELM的预测误差值。这表明经过CS算法改进的ELM模型预测精度有了明显的提高;CS算法的全局搜索能力要优于传统的GA算法。还可以看出,在预测误差方面,传统的DBN略差于本文提出的模型。但是在预测误差的方差方面,CS-ELM要明显优于其它3种模型。对于NMSE的方差,CS-ELM处于10-8数量级,而DBN的方差处于10-7数量级,CS-ELM的方差明显要小于DBN的方差,且也小于GA-ELM和ELM的方差。对于MAPE的方差,很清楚的可以看到本文提出的模型的方差时最小的。这说明CS-ELM的预测结果波动性小,模型稳定性好。 在运行时间方面,见表2。CS-ELM算法耗时明显少于GA-ELM和DBN算法。但是,CS-ELM与ELM相比,训练所需的时间要长一些。由于ELM模型的输入权值和阈值 是随机生成的,寻找最优的隐层节点数、输入权值和阈值可以提高模型的泛化能力。本文提出的模型是以训练时间为代价来提高模型的预测性能,故而在训练时间方面高于ELM模型。 表2 模型时间对比 2.1.3 模型举例 为体现CS-ELM的普适性,本文选用在献[3]中用到的GBP/USD汇率进行预测,同文献[3]中采用的评价指标进行比较。表3是CS-ELM与文献[3]中提出的共轭梯度法改进的DBN模型对GBP/USD汇率预测结果作对比。 表3 CS-ELM与DBN对GBP/USD汇率预测结果对比 从表3中可得知,本文提出的CS-ELM,在RMSE和MAPE方面稍优于文献[3]中提出的共轭梯度法改进的DBN。此外在表3中可以看出,CS-ELM的方差明显小于文献[3],文献[3]RMSE的方差处于10-8数量级,CS-ELM的结果处于10-9数量级;而MAPE的方差明显优于文献[3]。所以CS-ELM的稳定性要优于文献[3]的DBN模型,而CS-ELM模型预测精度可以接受但有待提高。 CS-ELM模型在时间序的列多步预测中也具有理想的预测效果,选择本文2.1节中的2012年5月19日至2012年6月20日的整个乌鲁木齐市话务量数据。选取输入节点数m=26,预测未来的o1,o2,…,on(n≥2)的话务量数据。预测步数对预测精度的影响,如图4和表4所示,可以看出来随着预测步数的增加,预测精度越来越差。但是对于十步预测的预测时的NMSE=0.004 52、MAPE=6.494 429,依然可以清晰的看出未来数据的走势,说明CS-ELM模型对时间序列多步预测的效果良好。 图4 多步预测中步数与预测精度的关系 本文提出一种基于CS算法改进的ELM的时间序列预测模型,采用CS算法自适应地获取最优ELM的隐含层节点数及相应的输入其权值和阈值,避免了预测输入权值和隐含层偏差随机性对ELM预测的影响。话务量数据预测实验结果显示,本文提出的算法结构简单,预测精度高,并且预测稳定性要优于其它传统的算法。并以汇率数据为例验证了CS-ELM的预测性能。进一步,通过话务量数据的多步预测,可以看出CS-ELM在多步预测中也有较好效果。 表4 不同预测步数的评价指标值 但是,由于CS-ELM模型是以牺牲训练时间来提高预测性能,并且其预测误差略优于DBN,所以如何加快训练速度和提高预测精度将是下一步的研究重点。1.4 评价参数
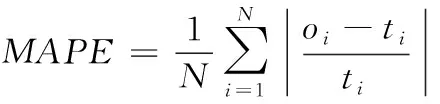
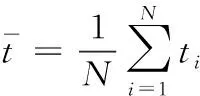

2 基于CS-ELM的时间序列预测
2.1 CS-ELM对时间序列的单步预测

2.2 CS-ELM模型的多步预测
3 结束语