基于超网络判别子图的阿尔兹海默症分类

郭 浩，张 帆，陈俊杰

(太原理工大学 计算机科学与技术学院，山西 太原 030024)

0 引 言

众多传统的功能脑网络的构建方法，如基于皮尔逊相关，偏相关的方法等，都存在一定的缺陷，即不能反应多个脑区之间的交互信息[1-4]。近年来超网络[5,6]模型被提出，恰好弥补了传统方法的以上缺陷。然而，现有基于超网络的分类方法中，如文献[5，6]分别在不同数据集上构建超网络，并提取局部脑区指标(局部聚类系数)作为特征进行分类。这样的特征提取方法可能会导致部分全局的拓扑信息丢失[7]。研究表明，子图特征被广泛地用于基于传统网络的脑疾病分类[8]，弥补了将脑区指标作为特征的不足。

鉴于此，本文提出了基于超网络判别子图的阿尔兹海默症分类方法。将子图特征用于超网络模型中，既能反应多个脑区之间的交互，又不丢失全局拓扑信息。具体地，首先采用稀疏线性模型构建超网络；之后提取超网络中的超边作为子图特征，采用HSIC(Hilbert-Schmidt indepen-dence criterion)，选择具有判别性的子图；最后，采用基于图核的支持向量机(support vector machine，SVM)进行分类。研究表明，本文所提出的分类方法可以有效地分类正常人和阿尔兹海默症患者。

1 数据采集及预处理

本研究是遵照山西医学委员会(参考编号：2012013)的建议，并且在征得所有受试者的一致同意。所有受试者均按照 Declaration of Helsinki签署了书面协议。采用德国西门子公司生产的3T超导型磁共振扫描仪对28例健康右利手被试、38例阿尔兹海默症被试进行静息状态的fMRI扫描。被试基本信息见表1。数据的采集工作是由山西医科大学第一医院完成的，所有的扫描工作由熟悉磁共振操作的放射科医生来完成。所有的阿尔兹海默症患者进行了全面的身体和神经检查，及标准实验室实验和神经心理学评估测试。

表1 被试基本信息统计

在扫描的过程中，扫描环境要求被试放松，闭眼保持清醒不能睡着，通过软海绵对被试头部进行固定，防止扫描过程中头部的移动。扫描参数设置如下：33 axial slices,repetition time(TR)=2000 ms,echo time(TE)=30 ms,thickness/skip=4/0 mm,field of view(FOV)=192×192 mm,matrix=6464 mm,flip angle=90°,248 volumes。由于磁化具有不稳定性，故丢弃前十卷的时间序列。

使用SPM8(statistical parametric mapping，SPM)[9]进行数据预处理。首先进行时间片校正和头动校正, 丢弃2例阿尔兹海默症组和1例正常组的样本，由于头动大于3.0 mm和转动大于3.0°，但其不包括在最终的28个样本中。对于校正图像，采用12维度的仿射变换进行优化，并将其蒙特利尔神经学研究所(MNI)标准空间中标准化为3 mm×3 mm×3 mm的体素。最后，进行线性降维和低频滤波处理(0.01 Hz-0.10 Hz)，以降低低频漂移和高频生理噪声。

2 方 法

2.1 超网络构建

在本文中，将静息态功能磁共振影像(rest-stating functional magnetic resonance imaging，r-fMRI)时间序列用稀疏表示[10]来构建超网络。具体地说，将X=x1,…,xm,…,xMT∈RM×d表示M个ROI(region of inte-rest)的被试，其中xm表示的是第m个ROI的脑区平均时间序列，d是时间序列的长度。之后，每个ROI的平均时间序列(即xm)被视为一个响应向量，并且能用一个其它M-1个ROI的时间序列的线性组合来表示，如下

(1)

其中，Am=x1,…,xm-1,0,xm+1,…xM表示除了第m个ROI(在其位置上放置一个全零的向量)的所有时间序列的一个数据矩阵，αm表示权重向量，量化了其它的ROI对第m个ROI的影响程度，并且τm∈Rd表示一个噪声项。在权重向量中的零元素表明了，对于时间序列的精确估计，其对应的ROIs是微不足道的。

一个稀疏学习用下面的目标函数来优化

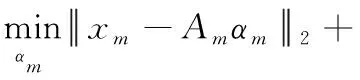
(2)

这是一个由l0-范数众所周知NP问题，并且通过解决下列目标函数的一个标准的l1-范数正则化问题[11]

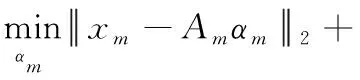
(3)

其中，λ>0是一个控制模型稀疏度的一个正则化参数。不同的λ值对应不同的稀疏度，并且λ值越大表明模型越稀疏。即在αm中更多元素为零。通过采用稀疏表示，得到一个脑区和其它部分脑区之间的相互作用，同时使无意义或虚假的相互作用为零。在估计一个脑区的时间序列上，在权重向量中对应零元素的脑区是被认为是多余的。这提供了一种建模方法，通过过滤掉多余的连接，构建一个脑区和其它剩余脑区之间的相互作用的模型。

在本文中，为了描述不同脑区之间的相互作用，对于每个被试，把每个ROI当作一个节点，通过稀疏表示来构建超网络，并且一条超边em包括一个中心ROI(即，第m个ROI)，和用等式(3)来计算权重向量对应的非零元素的其它ROI。为了反映脑区间的多阶相互作用信息，对于每个ROI(即节点)，生成了一组超边，而不是生成一条简单的超边，通过在一个具体范围内变化的λ。这里多阶表明不同的λ值决定了脑区之间的不同的阶的相互关系。换句话说，在等式(3)中，目标函数的λ值越大生成的解越稀疏，因此超边包含的节点较少。具体地，在本实验中，为了方便，λ值从0.1到0.9，增长的步长为0.1。值得注意地是，由于在等式(3)加权向量中相同时间序列的ROI有相同的值，因此，它们都将被包含在相应的超边缘，或联合排除。在实验中，采用SLEP包[12]来解决等式(3)的优化问题。

2.2 判别子图选择

本文利用超网络中的每条超边可以表示一个子图的特性，将超边作为超网络中的子图模式。然而 ，由于直接从超网络中提取超边作为子图特征，不仅导致特征的数量过多，而且其子图特征也具有较少的判别性。故而，对于分类而言，可能会降低分类准确率。鉴于此，本文进一步进行特征选择，将更具有判别性的子图模式作为特征用于分类。本文采用基于子网评价标准的HSIC[13]方法来选择具有判别子图作为特征。HSIC有两个重要的优势。其一，HSIC表示两个变量在核空间中的依赖性指标。其二，HSIC在经验估计上相对容易。具体地说，对于给定网络G=G1，G2，…，Gn,HSIC_Score的定义及公式如下

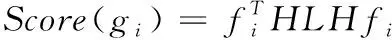
(4)

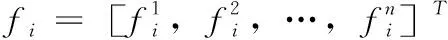
当HSIC_Score更高表明判别能力更强，故可以更容易地计算每个子图的判别能力。因此，分别从阿尔兹海默症患者和正常人的子图特征中选择HSIC_Score较高的前K个子图作为判别子图。

2.3 基于图核的SVM分类

2.3.1 图核

通常情况下，可以把核看作是两个被试之间的相似性指标，把原始空间的数据映射到一个高维的特征空间，使其特征空间中的数据更可能是线性可分的。给定两个被试x和x′，核则被定义为

kx,x′=〈φx,φx′〉

(5)

其中，φ是一个映射函数，可以把原始空间的数据映射到高维的特征空间。除了向量，核也可以被用于更加复杂的数据类型，比如图，其对应的核称为图核[14]。图核可以被看作是一个指标，用来衡量两个图之间的拓扑相似性。近些年，许多构建图核的方法被提出，其中包括基于路径[15]，基于子树核[16]等。在本文中，采用Weisfeiler-Lehman子树核来构建图核，其基于Weisfeiler-Lehman同构测试[16]。给定两个图，Weisfeiler-Lehman测试的基本过程如下：如果这两个图是无标签图(即图的每个顶点是没有分配标签的)，首先将每个顶点的首标签是与该顶点连接的边的数量。然后，在每次迭代中，每个顶点的标签是基于它之前的标签和它的邻居顶点进行更新。换句话说，将每个顶点更新的顶点标签的排序集压缩为新的且更短的标签集。重复这个过程，直到每个顶点的标签集是全部相同的，或者迭代次数达到预先设定的最大值。

给定图G和图H，∑0是G和H的节点标签的初始集，∑i是在图G和图H中Weisfeiler-Lehman算法的第i次迭代之后至少出现一次作为节点标签的字母集。假设所有的∑i={σi1,σi2,…,σi∑i}两两不相关。在图G和图H上h次迭代的Weisfeiler-Lehman子树核则被定义如下

khG,H=〈φhG,φh(H)〉

其中

φh(G)=(C0G,σ01,…,C0(G,σ0∑0),…,
ChG,σh1,…,Ch(G,σh∑k))
φh(H)=(C0H,σ01,…,C0H,σ0∑0,…,
ChH,σh1,…,Ch(H,σh∑k))

(6)

在本文中，CiG,σij和CiH,σij是节点标号σij在第i次迭代中分别出现在图G和图H中的次数。

2.3.2 分类模型

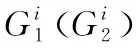
算法1：基于图核的分类

输入：

判别子图集DS1和DS2，被试集T

输出：

分类准确率acc

(1) for eachG∈Tdo

(2) fori=1:kdo

(5) endfor

(6) 把G分给具有较高图核值的类；

(7) endfor

(8) 计算被试集T上的分类准确率acc

为了评估所提方法的性能，采用十折交叉验证的方法进行验证。具体来说，在每一次迭代中，10%被试作为测试集，其余的90%被试被作为训练集，并且对每个被试重复此过程。采用分类准确率作为量化指标来评价该方法的实验结果，其衡量了预测正确的类标签的有效性。另外，利用稀疏表示方法构建超网络时，依据研究现状[6]，将λ的值设置为{0.1,0.2,…,0.9}，从而对每个被试构建成一个90×810的超网络。将超边视作子图模式，首先提取正常组和阿尔兹海默症组的子图模式，之后分别计算两组中每个子图模式的HSIC_Score，选取每组中HSIC_Score值较高的前K个子图模式作为判别子图，实验结果表明，正常组和阿尔兹海默症组分别选取15个判别子图时得到较高准确率92.3%。虽然在选取不同数量的判别子图时会导致分类的准确率发生变化，但在判别子图的数量控制在20-50个内时，平均的分类准确率基本达到了85%以上。

3 结果与讨论

本研究对子图特征进行了进一步的分析，将选取的30个判别子图中出现的脑区的次数进行排序，选取了发生次数较高的前15个异常脑区进行分析，图1(a)表明了这15个异常脑区在大脑中的分布情况，其节点大小表示该脑区在两组的判别子图中发生的次数之和，节点越大表示该脑区在两组判别子图中发生的次数越多。图1(b)表明了这15个异常脑区分别在AD组和NC组的判别子图中发生的次数，其中AD表示阿尔兹海默症，NC表示正常被试。

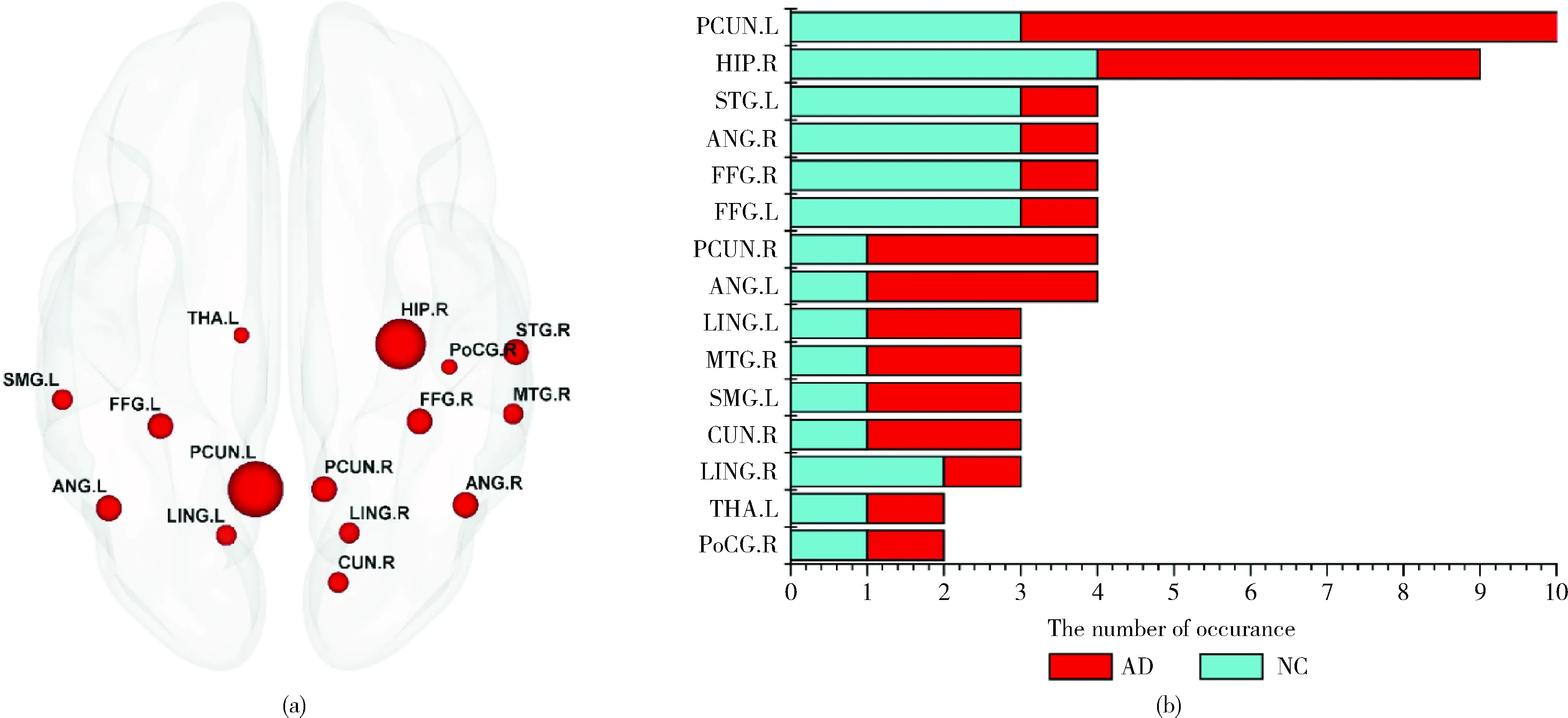
图1 异常脑区的分布情况

此外，表2中将这15个判别脑区的次数进行了由大到小进行了排序，且列出了其对应的英文缩写及中文名称。

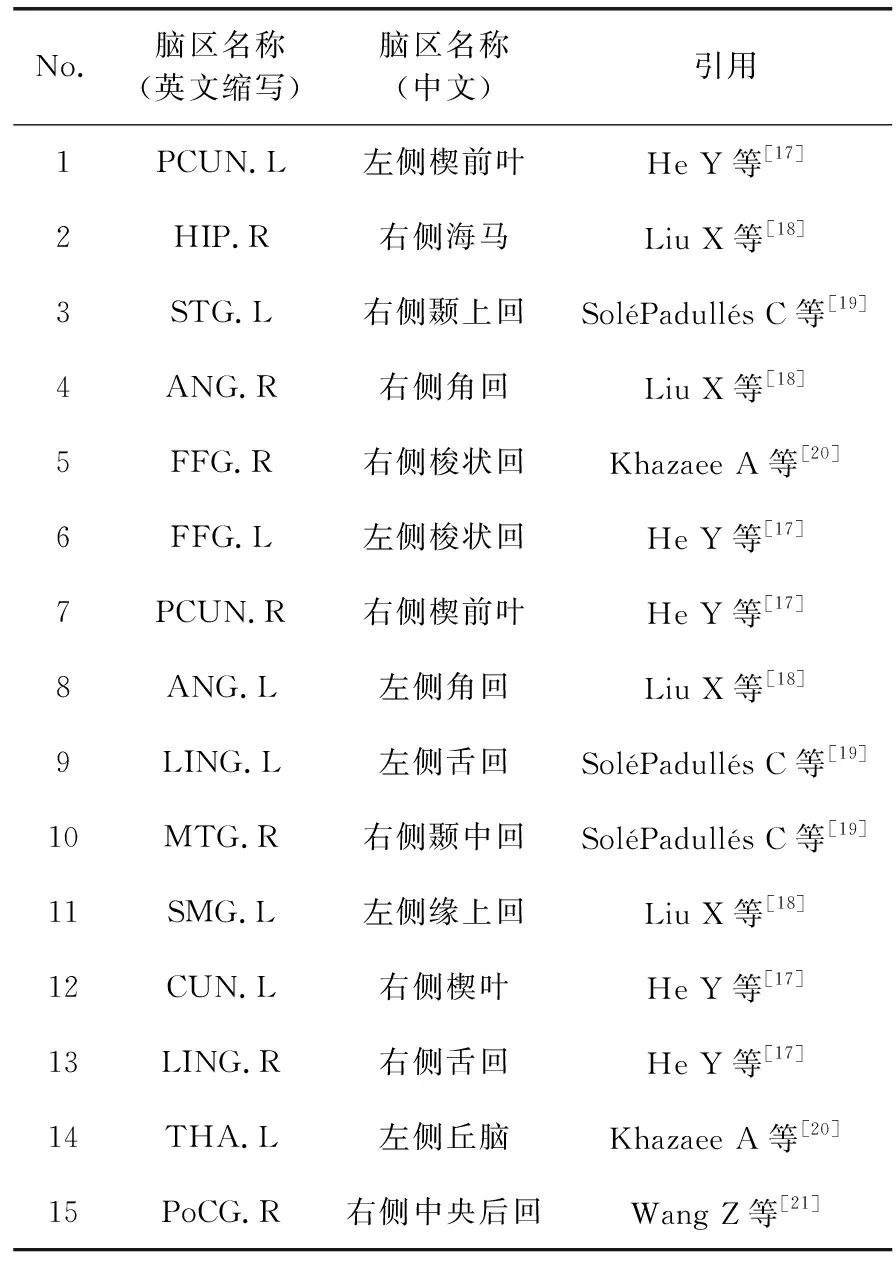
表2 TOP15异常脑区

本文采用判别子图作为特征进行分类的结果表明，涉及的异常脑区主要包括楔前叶，海马，海马旁回及颞叶部分区域等阿尔兹海默症病发的重要脑区，且实验结果与前人的研究保持一致[17-21]。

最后，将本文提出的方法与传统的方法相比，结果如表3所示。其中，Chen G等[22]采用传统的基于皮尔逊相关的方法构建脑网络，在特征提取部分，用脑区特征进行分类。而Jie B等[5]则在构建超网络的基础上，同样地，提取局部脑区特征进行分类。此外，Du J等[23]在传统网络的基础上，直接采用子图特征，并用基于图核的SVM进行分类获得的分类性能见表3。本文的方法是在构建超网络的基础上，将判别子图作为特征，采用基于图核的SVM进行分类。实验如表3所示，表3表明了本文提出的基于超网络判别子图的阿尔兹海默症分类研究方法，其分类性能相对有所提高，可以有效地用于阿尔兹海默症患者的分类。其潜在的原因在于该方法不仅反映了多个脑区之间的高阶信息，而且保证了完整的网络拓扑结构信息。

4 结束语

针对与传统的构建功能连接网络方法相比，超网络可以反应多个脑区之间的交互作用，以此来提高疾病的分类准确率。但是，目前的基于超网络的分类方法，基本是采用传统的脑区特征，然而其存在一个明显问题，即丢失连接网络中一些有用的拓扑信息。为此，本文提出了基于超网络判别子图的阿尔兹海默症分类。首先，采用稀疏线性回归模型，构建超网络；然后，将超边作为子图模式，采用HSIC方法选择判别子图；最后，采用基于图核的SVM进行分类。本文结果展示了将判别子图作为特征进行分类，从而检测到的异常脑区，与前人得出的异常脑区保持一致。此外，与传统分类方法比较，结果表明该方法的优越性。其一，考虑了多个脑区之间的交互关系，以反映脑区间的高阶交互信息。其二，将判别子图作为特征，以保证网络的拓扑结构信息的完整性。实验结果表明，在阿尔兹海默症的分类上，与传统方法做对比，该方法不仅提高了分类准确率，而且也发现了其相关的病发脑区。在本文的研究中，也有局限性。即数据集的大小，虽然本文现在使用的是较小的阿尔兹海默症的数据集。但在未来的工作中，将会用更大的数据样本来评估该方法的性能。

表3 不同特征提取分类方法的性能