基于相关向量机的锂离子电池剩余寿命预测

李 赛，庞晓琼，林慧龙，王竹晴

(中北大学 大数据学院，山西 太原 030051)

0 引 言

为了减少因电池故障带来的人身伤害以及财产损失[1-3]，准确预测电池的剩余使用寿命(remaining useful life，RUL)成为了现有研究的热点和难点[4]。

目前，将锂离子电池的RUL预测的方法主要分为基于经验的统计方法以及基于性能的方法两大类[5]。后者应用比较广泛，主要有基于物理模型方法，数据驱动方法以及融合方法[2]。然而在实际应用中，物理模型的电子系统通常复杂，因此其适用性较差。基于数据驱动方法中相关向量机算法优点是它在贝叶斯框架下构建学习机，对核函数选择没有约束，其输出结果能够反映目标值的不确定性，有很好的泛化能力，算法简单，容易实现[6]。

本文以容量作为性能参数采用相关向量机(relevance vector machine，RVM)算法对锂离子电池的剩余使用寿命进行直接预测，得到该电池的剩余寿命的预测值和预测置信区间。

1 相关向量机模型预测原理

相关向量机是Tipping基于贝叶斯框架提出来的[7]。RVM函数形式与支持向量机相同，且均是由核函数将低维非线性向高维线性问题转化，完成高维特征空间中最优分离超平面的构造，使得平面上较难分的非线性数据分离[8]。

1.1 相关向量回归描述

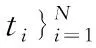
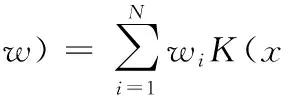
(1)

K(·)是核函数，wi表示RVR的权值N是样本数。

假定输出值独立，数据的噪声用εi表示，且εi～N(0,σ2)，则带有噪声的模型，我们定义为下式

ti=y(xi,w)+εi

(2)

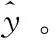
因此，相关向量回归(relevance vector regression，RVR)表达式为下式

t=φw+ε

(3)

其中，w=(w0,…,wN)T，N+1维列向量,表示RVR的权值；φ是N×M的设计矩阵且φ=(φ0，…,φN)T；φi(xi)=[1,K(xi,x1),…,K(xi,xN)]，i=1,2,…,N；K(·)是核函数。

由于前文中假设ti独立，得到训练集的似然函数是

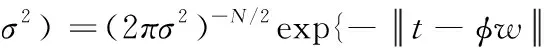
(4)

把超参数引入每一个权值中。相关向量机通过为每一个权值定义了高斯先验概率分布来约束超参数

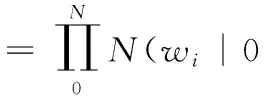
(5)

其中，α={α0,α1,…,αN}是N+1个超参数。

1.2 贝叶斯过程推理

所有未知参数有后验公式

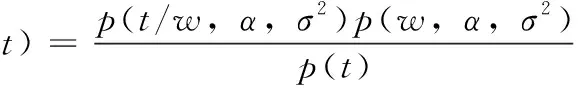
(6)

输入一个新的观测值x*，得到对应的预测目标值为

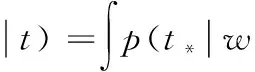
(7)

因为p(w,α,σ2/t)=p(w/α,σ2,t)p(α,σ2/t),所以

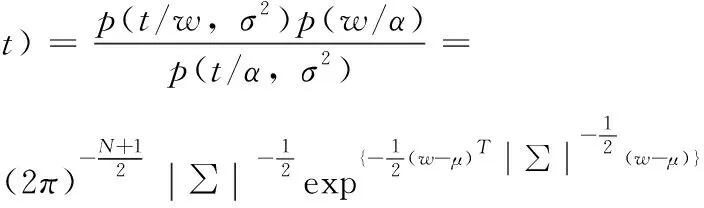
(8)

其中，权重的协方差方差∑=σ2I+ΦA-1ΦT，A=diag(α0,α1,…,αN)，均值μ=∑ΦTBt(B=σ2I)；

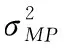
因为p(α,σ2/t)∝p(t/α,σ2)p(α)p(σ2),求出p(t/α,σ2)的最大值即可。

根据

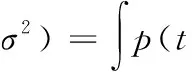
(9)

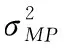
1.3 超参数的更新及RUL预测

(10)

式中:μi是第i个后验权值的均值，∑ii为后验方差矩阵的第i个对角线元素。

对式(10)求偏导得

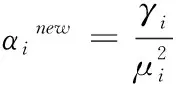
用相同的方法求出噪声方差

(11)

通过迭代计算式(10)、式(11)，很多超参数会在进行重新估计的过程中趋于无穷大，甚至无限接近于0，所以与之对应的核函数可以删除，进而达到稀疏化[10]，从而获得使α和σ2的最大解析表达式。

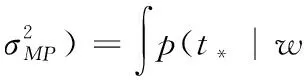
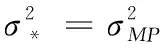
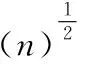
2 仿真实验设计与分析对比

2.1 仿真实验设计

实验目的：为对本文提出的锂离子电池RUL预测方法进行有效的验证，将电池的容量数据作为该实验的样本数据进行RUL 预测，从而对本文所提方法的预测能力进行评估。

实验方法：本文的实验对象选取为NASA提供的公开数据集(B5、B6、B18)，这3种电池的型号和额定参数均相同。设定预测起始时刻，用RVM预测法进行RUL预测。

实验步骤：本文选择的容量数据，前60周期用于训练模型的超参数， 从60周期开始作为预测起始时刻，经仿真实验，得到对电池容量预测的退化曲线以及预测上限和下限。当电池随充放电不断进行，容量达到寿命结束点(end of life，EOL)，即电池容量衰减达到额定容量的70%左右时，实验终止。实验时电池的失效阈值设置为1.38 Ah。由于B7电池容量未退化到 1.38Ah，故实验未采用。最后将预测结束点的循环周期数及其置信区间转化为RUL值和RUL置信区间，与真实的RUL 进行对比与分析。

2.2 实验结果分析

2.2.1 容量退化曲线

根据容量的真实值完成4个型号电池的退化曲线，如图1所示。

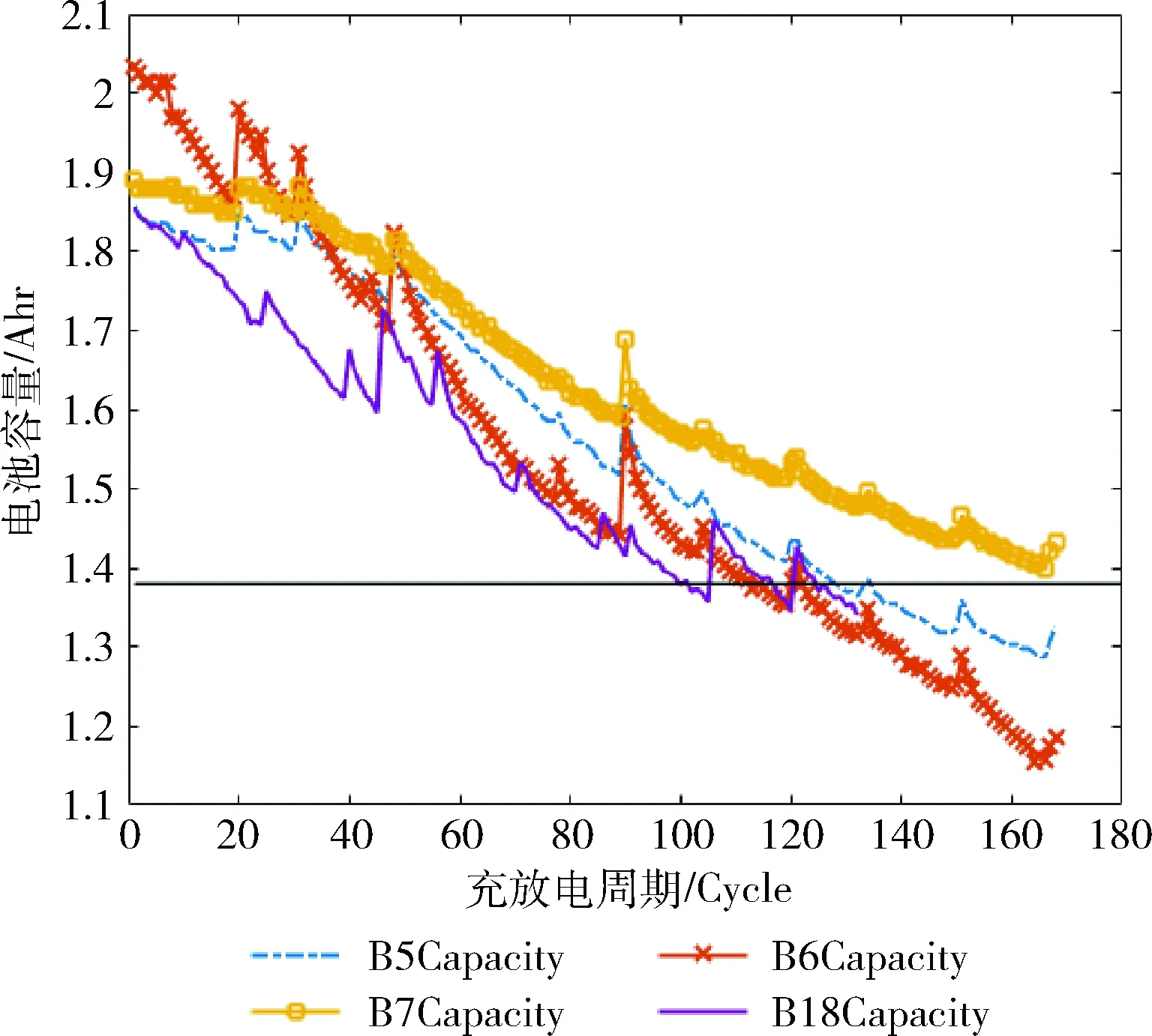
图1 电池容量退化曲线(B5、B6、B7、B18)

从图1可知，锂离子电池的容量随着充放电次数的增加而减小。其实在电池的使用过程中，导致其性能退化的原因还有很多种，如温度升高的速度加快、内阻变大等[11]。

2.2.2 RUL预测

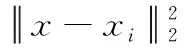
B5、B6、B18电池的预测起始时刻设为60。首先对B5电池进行实验，得到如图2所示的结果。

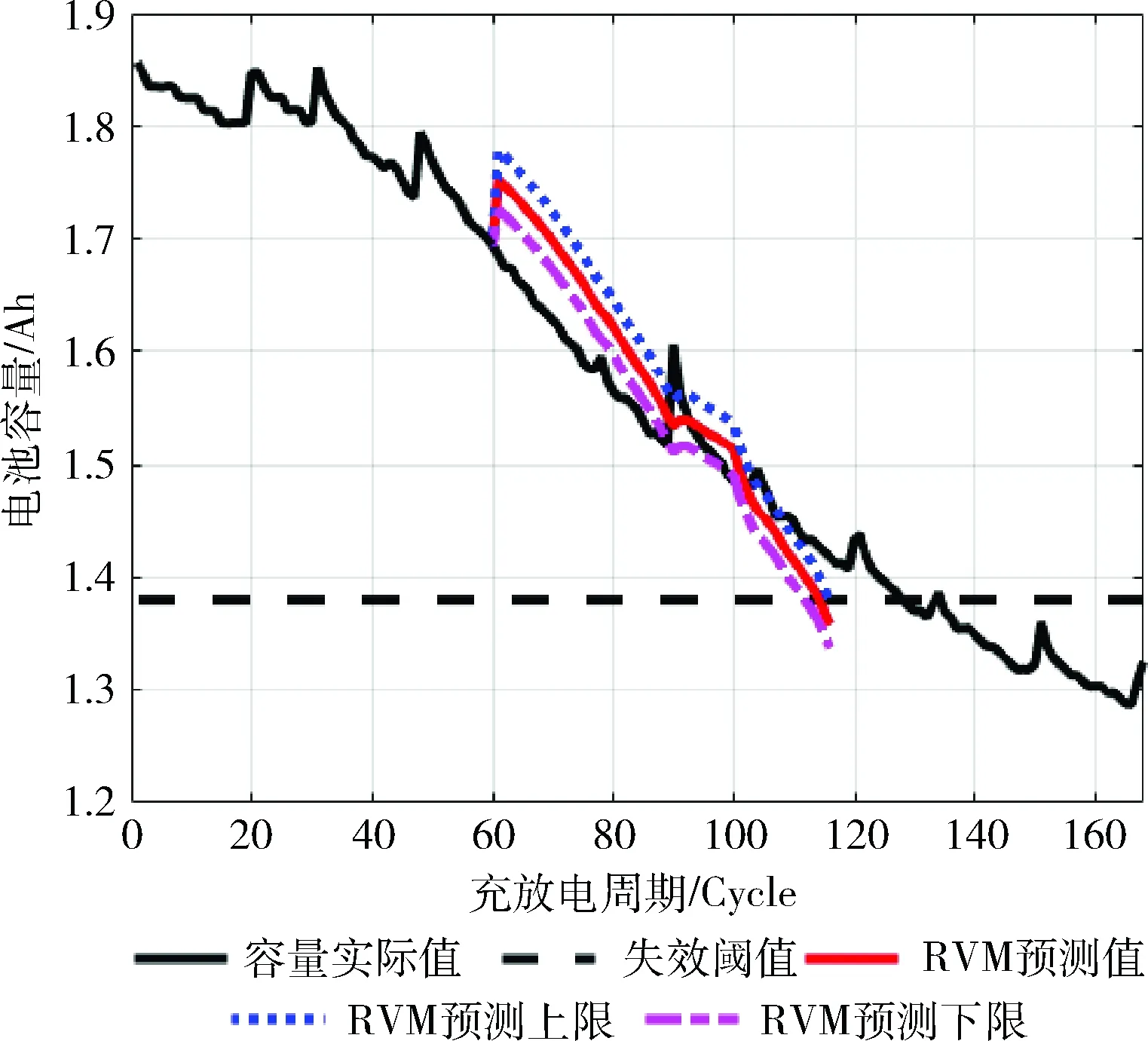
图2 RVM预测曲线(B5)

在图2中，黑色虚线代表该电池的失效阈值，黑色实线代表该电池的实验测量数据，实线曲线表示利用相关向量机的时间序列算法得到的该电池的预测值。点线和点划线分别表示RVM算法对容量的预测上限和预测下限。

为了进一步的验证该算法的有效性，我们分别B6和B18电池进行实验。

对B6电池进行实验，得到如图3所示的结果。

图3 RVM预测曲线(B6)

对B18电池进行实验，得到如图4所示的结果。

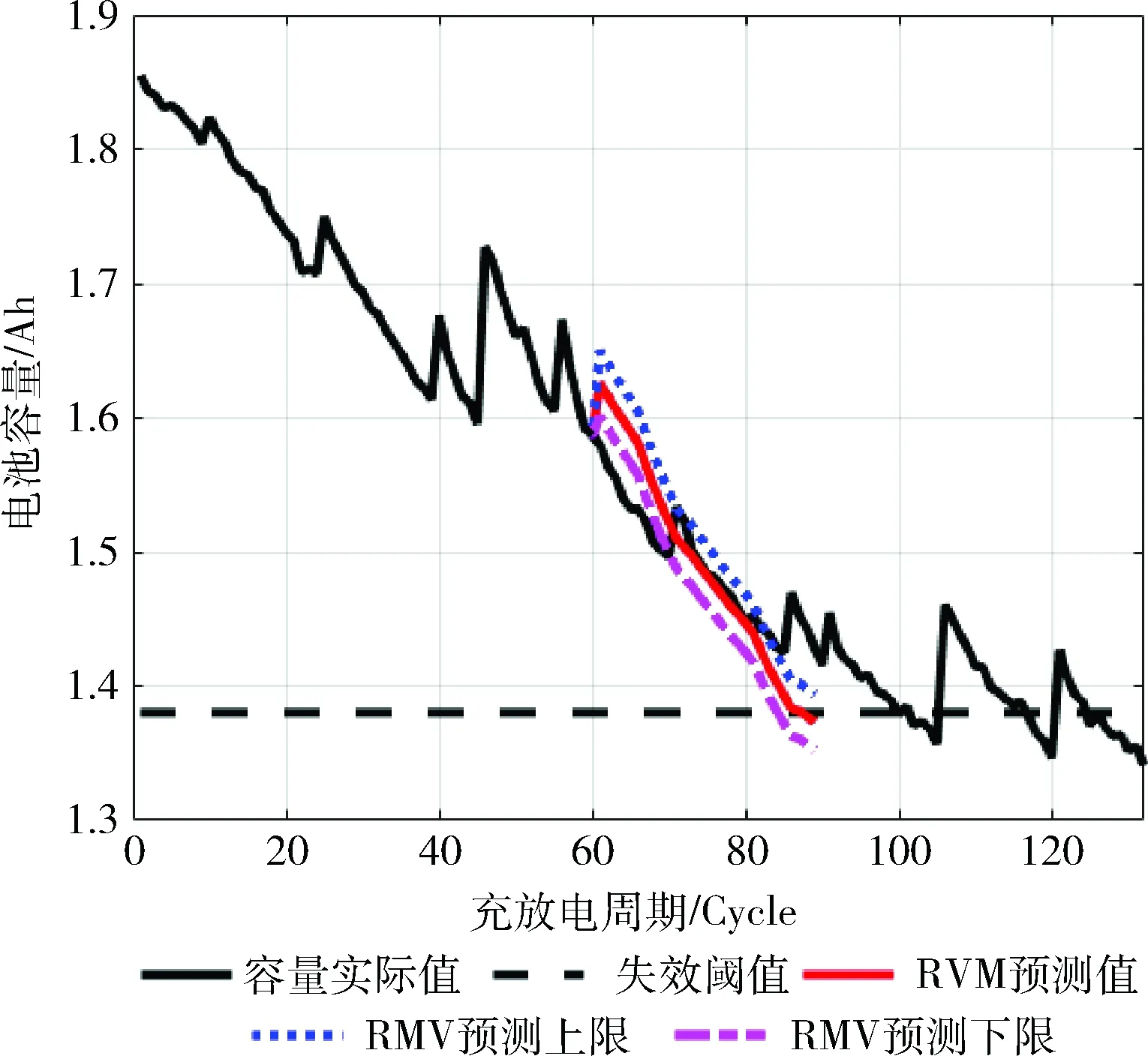
图4 RVM预测曲线(B18)

从以上3个图中，我们可以看出，B5、B6、B18电池预测起始点均为第60个周期，寿命结束点的真实值分别是129、113和100周期，预测结果分别是114、97和87周期。B5电池寿命的预测下限和上限分别是116和112周期；B6电池寿命的预测下限和上限分别是99和95周期；B18电池预测上限和下限分别是89和84周期。具体结果见表 1。

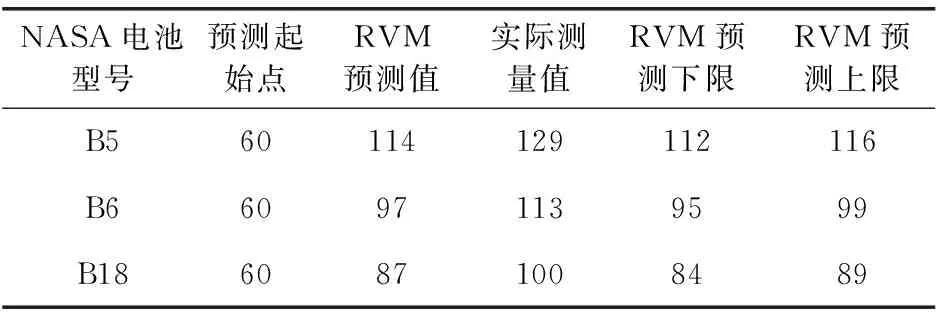
表1 RVM预测值及其预测上限和下限

2.3 实验分析

本文中RVM超参数的设置对容量的预测结果有直接的影响，比如样本数据的多少和高斯核函数中核宽度的设置决定了模型的稀疏性和精确性[12],本文分别对B5、B6、B18电池进行实验，它们的起始预测周期均为60周期，电池的真实使用寿命终点分别为129、113和100周期,并仿真出容量预测值，见表2。

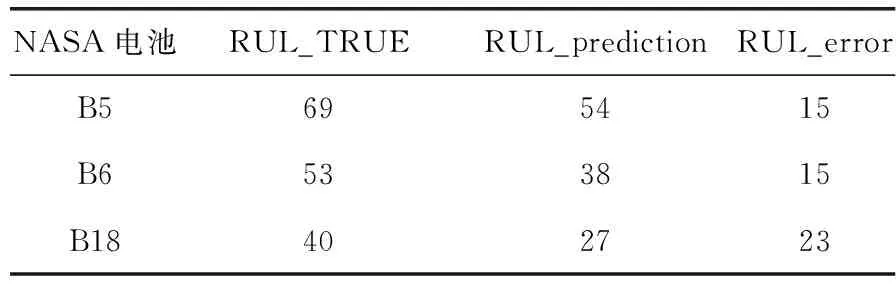
表2 采用RVM的RUL预测结果

在表2中，RUL_prediction表示利用RVM预测所得的锂离子电池的剩余循环使用寿命，RUL_error表示RUL的绝对误差值，定义为：

RUL_error=RUL_prediction-RUL_true其中，RUL_true表示设置预测起始点后电池的真实剩余循环使用寿命。

由表1得出，B5、B6、B18的RUL_true分别是129-60=69周期、113-60=53周期和100-60=40周期。采用相关向量机算法预测的剩余使用寿命分别是RUL_prediction=114-60=54个周期、RUL_prediction=97-60=37个周期和RUL_prediction=87-60=27个周期。预测的循环使用寿命误差分RUL_error=69-54=15、RUL_error=53-37=16和RUL_error=40-27=13。

2.4 相关向量机算法与扩展卡尔曼滤波算法对比实验分析

为了进一步说明相关向量机算法的有效性，现在将该算法和扩展卡尔曼滤波(extended kalman filter，EKF)的RUL预测周期和预测误差进行对比，预测周期见表3。

从表3中可以得到，B5、B6、B18号电池在相同的预测起点第60个周期时，相关向量机方法对锂离子电池的RUL预测结果分别为54、38和27个周期。扩展卡尔曼滤波方法得到的B5电池预测结果分别为49个周期，B6电池仅为24个周期，B18电池为14个周期。

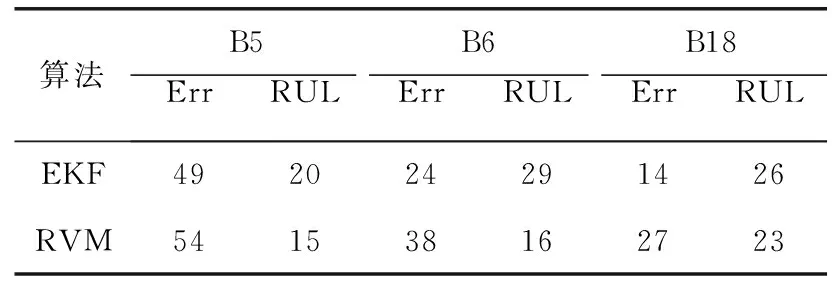
表3 两种方法的RUL预测结果及误差对比

为了较准确对两种算法分析对比，引入绝对误差均值(mean absolute error，MAE)与均方根误差(root mean square error，RMSE)。

式中:n是预测数据的长度，x_real(i)是第i次预测时的真实容量值，x_m(i)是第i次预测的容量值，该电池平均绝对误差和均方根误差见表4。

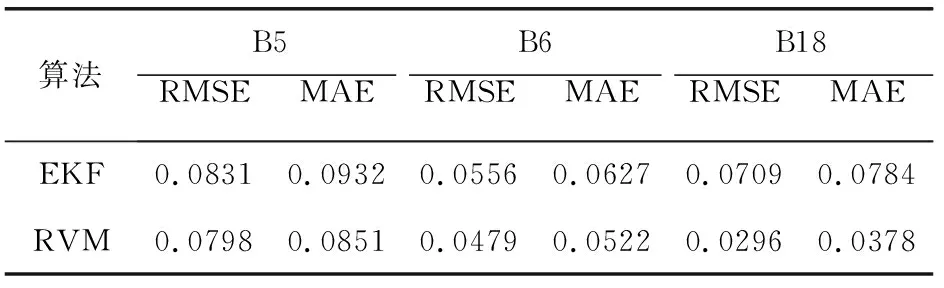
表4 两种方法的RUL预测误差

从表4中可以得到RVM算法的误差均小于EKF的误差，即RVM算法的预测精度高于EKF的预测精度。

3 结束语

锂离子电池已经被应用在生活、工业等领域，其工作性能状态的在线监测和预测性维护已成为研究热点，并已在电子系统故障预测和健康管理技术领域形成新的研究热点。

本文借鉴了时间序列多步预测的递推计算的思想，实现了锂离子电池RUL预测，并给出了电池寿命的置信区间，充分考虑了递推过程中预测不确定性的传递问题。与扩展卡尔曼滤波算法相比,本文的独特之处为该算法输出的锂离子电池的剩余寿命分布能够更加有效地反映各种不确定性和随机因素,比较符合实际情况。