基于转矩协调分配的分布式驱动电动汽车稳定性控制

张细政 郑 亮

湖南工程学院电气信息学院，湘潭，411104

0 引言

车辆稳定性控制要求汽车行驶在一理想轨迹的同时，车辆状态始终跟随理想状态。近年来，将电机置于车轮内，车轮采用独立电机作为驱动源的新型分布式驱动电动汽车（distributed-driven electric vehicle，DEV）得到了广泛关注。在分布式驱动形式下，各轮驱动/制动转矩独立可控，只需结合汽车运行状态直接对电机施加控制，便可以精确地将转矩控制分配到每个车轮［1-2］。因此，获得可物理实现的纵向力与转矩，并将其协调地分配到4个车轮上，是实现DEV操纵稳定的关键性问题。

从已有研究文献来看，DEV稳定性控制多采用层次化的结构，控制上层为横摆力矩控制器设计，下层为横摆力矩的控制分配［3-9］。横摆力矩控制器完成横摆力矩的决策和计算，根据车辆当前状态与参考值的误差计算出所需的期望横摆力矩。控制策略开始采用一些现代控制方法，如滑模控制［3-4］、模糊与神经网络控制［5-6］、模型预测［7］和最优化方法［8］等。目前，大部分DEV的稳定性控制研究集中在横摆力矩控制器设计，研究比较成熟，基本都能实现优良的控制效果。这些方案在计算期望横摆力矩时，使用的控制变量是横摆角速度和质心侧偏角，而由于横摆运动和侧偏运动间的耦合关系，控制两变量所需的横摆力矩往往相反，单独依靠直接横摆力矩控制（direct yawmoment，control，DYC）很难实现两者的有效解耦，在极限工况下两者的冲突更加突出，车辆的稳定性受到较大影响［9-10］。由此，需要设计简单可靠的横摆与侧偏运动解耦方法以提高极限工况下的车辆稳定性。

期望横摆力矩由下层控制器精确地分配到各执行器上，形成车轮的纵向力和转向角。文献［11］基于前轮转角的前馈控制和车辆状态误差的反馈控制，仅采用简单的转矩平均分配法，稳定效果不佳。文献［12］以轮胎利用率为指标进行力的优化分配，但要求所有车轮可以独立制动、独立转向。文献［13］提出将纵向力分配问题等价为带有不等式约束的非线性规划问题，但所设计的逐点二次规划算法过于复杂。文献［14］在解决了纵向合力与横摆转矩可行域的实时估计基础上，通过合力计算与优化分配，构造了内环、外环结构的车辆稳定控制系统，但忽视了车辆的转向控制能力。文献［15］采用由计算总横摆力矩的运动控制器和优化各车轮驱动转矩的控制分配器组成的分层模块化控制框架，增强了汽车的侧向横摆和侧翻稳定性能，但该方法需要进行多次在线优化，运算复杂。分配的实质是一个有约束优化问题的求解，如何充分利用协调优化的技术优势，综合考虑执行器约束和车轮滑移率等当前工作状况，设计开发更为有效的稳定性控制系统是当前DEV动力学控制研究的重要内容。

本文在八自由度车辆模型基础上构造了层次化的DEV稳定性控制系统。

1 车辆稳定控制模型

1.1 车体仿真模型

本文的车体模型假设车轮始终接触路面，侧倾轴线在汽车中心平面上，忽略汽车的俯仰及垂直运动，共有纵向、侧向、横摆和侧倾4个自由度，再加上4个车轮自身的转动，采用八自由度非线性车辆模型进行稳定性分析与设计［16］，见图1。

图1 八自由度车辆模型Fig.1 Eight degrees of freedom vehicle model

车身纵向动力学方程为

车身侧向动力学方程为

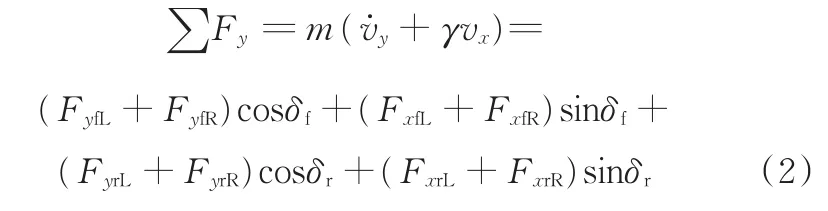
车身横摆动力学方程为

车身侧倾动力学方程为

车轮运动学方程为

由式（2）得车身侧偏动力学方程：

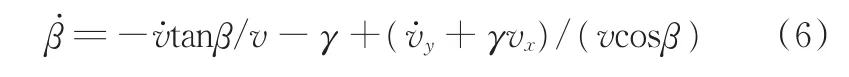
式中，v、vx、vy分别为质心、纵向和横向车速；δf、δr分别为前轮、后轮转向角；γ为横摆角速度；β为质心侧偏角；Iz、Ix分别为横摆转动惯量和侧倾转动惯量；φ为车身侧倾角；FxfL、FxfR、FxrL、FxrR、FyfL、FyfR、FyrL、FyrR分别为沿纵向、侧向的前左、前右、后左和后右轮胎力分量；下标f、r分别表示前后轮，L、R分别表示左右轮；Td，ij、Tb，ij（i=f，r；j=L，R）分别为车轮驱动力矩和制动力矩；m为整车质量；ms为悬挂质量；a、b分别为前轴、后轴与质心间的水平距离；tf、tr分别为前轮、后轮距；Bφ、Kφ分别为悬架侧倾角阻尼和单侧轮胎侧偏刚度；Jω、ωij、Rw分别为车轮滚动惯量、角速度和滚动半径；hs为簧载质量的侧倾力臂。

1.2 非线性轮胎模型

采用“魔术公式”轮胎模型模拟轮胎的非线性力学特性［16］，为简单起见，不考虑纵向力和轮胎回正力矩的作用，忽略曲线的垂直和水平方向漂移，轮胎侧向力

式中，D为峰值因子；C为曲线形状因子；α为侧偏角；E为曲率因子；B为刚度因子；系数ai（i=1,2,…，7）的值采用SAE-870421中的轮胎模型数据［17］。

轮胎附着力大小由近似摩擦圆限制，最大轮胎纵向力

式中，μ为路面附着系数。

由式（7）、式（8）知，在车辆行驶过程中，轮胎受到的垂直载荷对纵向力和侧向力有着重要影响，考虑汽车加速、减速及转向时汽车的载荷转移影响，前轴、后轴垂直载荷差为

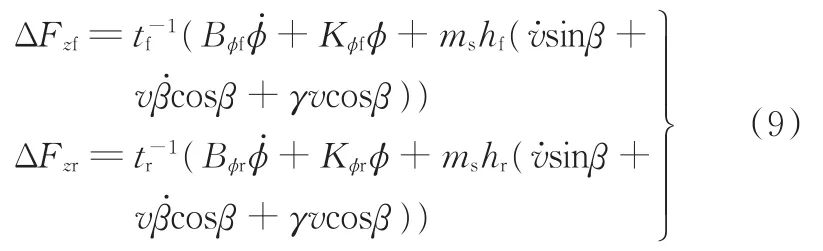
轮胎垂直载荷为

轮胎的侧偏角计算公式为

2 车辆稳定的分层控制器设计

基于分层控制思想，分三层设计控制系统：上层为横摆力矩控制器，中层为线性二次型调节器（LQR）优化分配器，下层为基于滑模变结构的滑移率控制器。

2.1 稳定性控制参考模型

为得到车辆横摆运动的期望值，本文采用二自由度车辆模型设计理想质心侧偏角βd和理想横摆角速度γd。对于质心侧偏角，应该尽量保持βd为零；而理想横摆角速度是要保证在某一车速下，驾驶员感觉其转向输入与车辆横摆角速度间成近似线性关系，以减小操纵难度。不考虑各轮轮心的纵向速度差异，参考模型的稳态响应为［17］

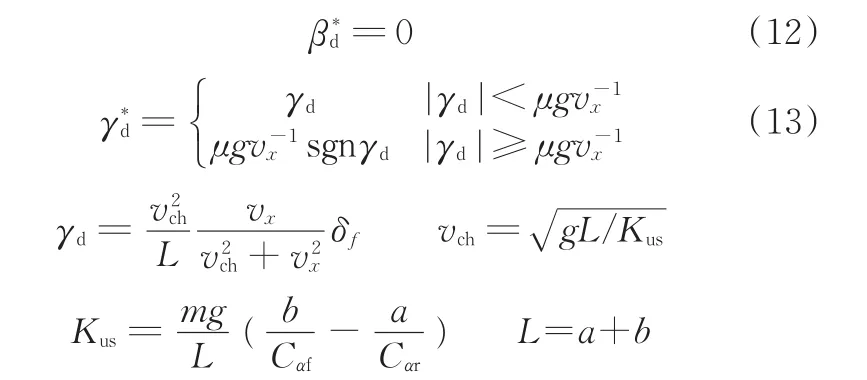
式中，vch为稳定性参数；Cαf、Cαr为前轴、后轴轮胎的侧偏刚度。

2.2 横摆力矩LQR控制器

当车辆的实际横摆角速度和质心侧偏角与理想的横摆角速度和质心侧偏角出现偏差时，上层控制器在汽车上施加一给定的附加横摆力矩来完成对车辆行驶状态的纠正，使其始终跟随参考模型所产生的理想值。考虑如下积分二自由度车辆控制模型：

采用LQR方法设计状态反馈控制律：

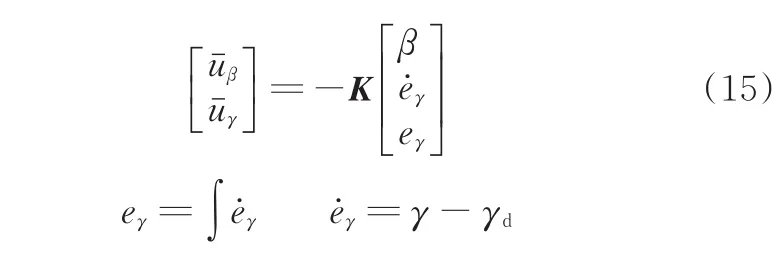
给定闭环控制系统式（14）的期望极点，利用极点配置方法，即可求出闭环反馈增益K。

不同于其他基于二自由度车辆模型的稳定性系统［1，4，7］，式（14）中控制矩阵的结构特点表明等效控制两分量已经解耦，可以独立设计；同时，式（15）的控制量设计引入了积分模型，能有效改进横摆角速度跟踪时的稳态误差。

2.3 控制分配器

计算出的等效控制量需要在轮间进行分配，即根据车辆行驶状态的识别、驾驶员转向盘的检测等，判断车辆在哪个轮上或哪几个轮上分配横摆力矩，通过控制分配器向4个轮毂电机发出驱动或制动指令，对车轮进行转矩调节，最终转化为轮胎与地面的相互作用力，以此来达到保持车辆稳定的目的。对于DEV电动汽车，车辆由4个轮毂电机进行驱动，前后轴均可独立转向，整个系统可通过多种灵活的输入组合形式来完成等效横摆力矩的轮间分配。考虑如下分配：

式中，B为控制输入矩阵；u为实际控制输入量。

本文采用前后轮独立转向、转矩独立控制的DEV，则有

式（16）中存在执行器的冗余。控制分配器的作用是在同时考虑地面附着条件限制和执行器位置/速率限制的情况下，完成各控制输入量的最优分配，其本质上是一个有约束的多变量优化问题。等式（16）的控制量分配可转化为有约束的二次优化问题，即

式中，Q为对称正定矩阵；C为线性系数矩阵；ulb,i、uub,i为执行器约束的上下界。

式（17）的优化问题既包含了车辆稳定性控制中对状态误差的要求，又体现了对独立制动产生的汽车横摆力矩的要求。观察控制矩阵B的结构，发现控制输入[δfδr]直接作用并决定了质心侧偏角和横摆角速度，具有更大的控制效果；而四轮驱动力Fx，ij仅直接作用在横摆角速度状态方程上，经由两个状态间的耦合作用来间接对质心侧偏角施加影响。这种耦合可能使优化过程中控制目标间冲突，尤其是在执行器故障的情况下，需要优先保证横摆角速度的稳定性控制。在式（16）中引入虚拟控制量τ，新的状态方程为

其中，κ为控制矩阵。虚拟输入uˉ中通过引入τ，增加了控制自由度，给定实际控制输入u，在实现横摆角速度跟踪优先控制的同时，可以放宽对质心侧偏角的等式约束，从而达到两个状态间解耦目的，因而，κ值选择时，要求γ→τ的直流增益为零。由式（18）求得输入τ对状态γ的传输函数：式中，L表示拉普拉斯变换。

由式（19）可求得：

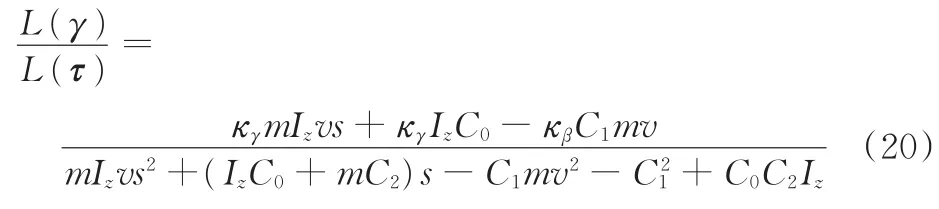
令传输函数式（20）的直流增益为零，则有κγIzC0-κβC1mv=0，求得κβ=1，则优化问题式（17）转化为如下模型

2.4 车轮滑模滑移率控制器

车轮纵向力与轮胎滑移率直接相关，在给定期望滑移率下，设计滑移率控制器（slip rate controller，SRC）来调节各车轮纵向力大小。在车辆转向和横摆运动的影响下，沿车轮坐标系的轮心纵向车速和滑移率分别计算如下：

在定侧偏角下，轮胎纵向力会随着纵向滑移率的增加而先快速增大，在临界滑移率σ∗处达到峰值，滑移率再继续增加后轮胎纵向力反而减小。

然而，在一定的垂直载荷下，由于车轮附着力的限制，当目标轮胎纵向力Fx,ij过大时，按式（24）控制车轮转矩会使得实际滑移率超出临界滑移率，从而造成车轮抱死和纵向力减小，因此，当实际滑移率较大时，需要采取滑移率控制策略来调节电机转矩，从而限制车轮滑移率。

制动工况下，构造以滑移率误差为变量的滑模函数为

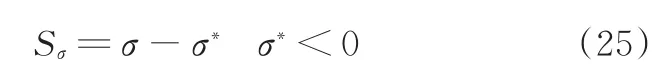
选取Lyapunov稳定性函数

轮胎纵向力可表示为线性部分和非线性增量之和，即

式中，Cσ为轮胎工作在线性区域时的纵向刚度；ΔFx,ij为非线性增量，且满足0≤ΔFx,ij≤；为非线性增量最大值。

结合车轮运动方程式（5）和式（27），可得

控制器稳定的必要条件是滑动模态到达条件需要得到满足，即

将式（28）代入式（29），有

当车辆制动行驶时，设计车轮转矩控制量

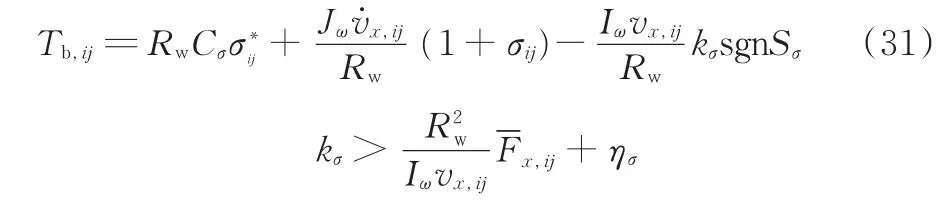
式中，kσ滑模增益。由式（30）和式（31）知，当Sσ≠ 0时，V̇＜ 0，而V 正定，则此时整个滑移率误差动态是一致渐近稳定的，零点是系统的一个稳定点。

同上，加速工况下，设计车轮转矩控制量

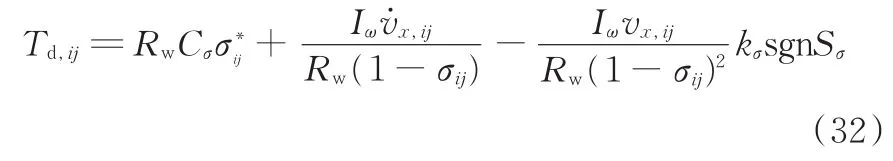
设计的滑模滑移率控制器的工作原理见图2。

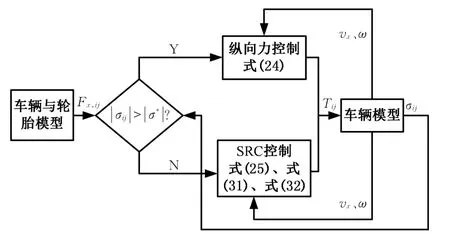
图2 滑模滑移率控制器工作原理Fig.2 Principle of sliding mode slip controller

3 仿真结果与分析

在MATLAB/Simulink软件环境下构造车体和轮胎模型，并对控制系统进行仿真。选取DEV轿车参数为：a=1.013m，b=1.702m，Tf=1.554m，Tr=1.534m，m=1.401kg，Ix=550.2 kg ·m2，Iy=2 587.1kg ·m2，Iz=2 677.2 kg ·m2，hs=0.582 2m，hf=hr=0.127m，Kφf=4 297.2N·m/rad，Kφr=3 724.2N·m/rad，Bφf=900N ·m ·s/rad，Bφr=850N ·m ·s/rad，Cαf=113.2kN·m/rad，Cαr=90.2kN·m/rad。

闭环系统期望极点设置为［-7 -2+5i-2-5i］，求得反馈增益K=［0.466 7 -0.926 8-0.008 3 0.042 8 3.993 7 29.000 3］。分层控制系统见图3。

图3 分层控制系统框图Fig.3 Hierarchical control system block diagram

分别在转向角阶跃输入、正弦输入和转向器故障3种工况下进行仿真分析。为便于比较，仿真时给出了本文设计的优化分配（O）、DYC控制（DYC）和无控制（w/o）下的稳定性能曲线。

3.1 阶跃转向工况

图4～图8所示为车速80 km/h、路面摩擦因数0.8，转向盘阶跃输入（转角2π/3）时的仿真结果。仿真结果显示，无控制时车辆的横摆角速度γw/o和质心侧偏角βw/o很快达到危险的临界值，表明此时车辆已经接近失控，需要采取相应的控制策略才能保证车辆的期望转向。

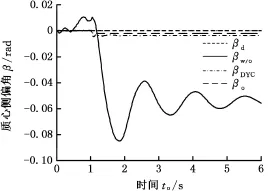
图4 质心侧偏角响应曲线（阶跃转向工况）Fig.4 The responses of centroid side-angle（step steering）

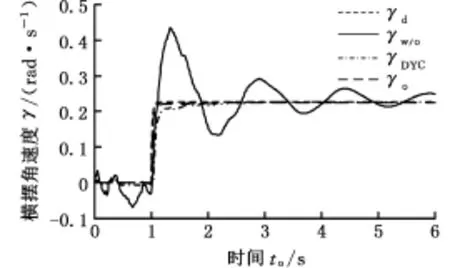
图5 横摆角速度响应曲线（阶跃转向工况）Fig.5 The yaw rate responses（step steering）

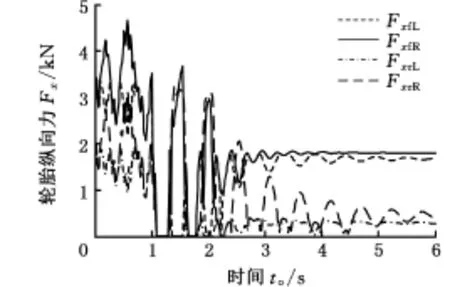
图6 四轮轮胎纵向力（阶跃转向工况）Fig.6 Four-wheel tire longitudinal forces（step steering）

图7 四轮轮胎滑移率（阶跃转向工况）Fig.7 Four-wheel tire slip rates（step steering）

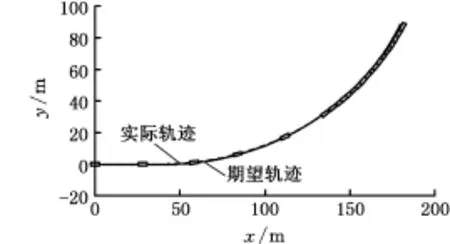
图8 车辆行驶轨迹（阶跃转向工况）Fig.8 The vehicle desired and actual rajectories（step steering）

从图4、图5中可以看出，在采取DYC控制和优化分配后，两种控制器的横摆角速度和质心侧偏角都能较好地跟踪理想模型，使车辆稳定转向。相较于DYC控制，本文设计的优化分配方法通过在四轮施加适当的制动力矩，车辆的横摆角速度响应γo能更好地跟踪理想横摆角速度γd，并稳定在0.226 rad/s左右；同时车辆质心侧偏角βo也得到很好的抑制，并稳定在理想的零侧偏角范围内，表明该控制系统有很好的稳定性。图6给出了四轮轮胎的纵向力。图7为四轮滑移率绝对值，在转向开始后，滑移率开始上升，但在滑移率控制器的作用下始终小于0.2；同时，由图可见四轮中左后轮滑移率相对较大，而右前轮的滑移率相对较小，反映了车辆左转时车速不变情况下左后轮轮速较小、右前轮轮速较大的实际情况。图8给出了本文优化分配方法下车辆质心的期望轨迹、实际轨迹和航向，可见车辆能很好地跟踪理想行驶轨迹。

3.2 正弦转向工况

图9～图13所示为车速80 km/h、路面摩擦因数0.8，转向盘正弦输入（转角±π/2，频率0.25 Hz）时的仿真结果。结果显示，无控制时车辆的横摆角速度γw/o已不能跟踪理想单移线行驶，质心侧偏角βw/o则很快达到极危险的临界值，车辆此时已经失控，需要进行必要控制才能保证车辆的单移线变道行驶。

图9 质心侧偏角响应曲线（正弦转向工况）Fig.9 The centroid lateral responses（sinusoidal steering）

图10 横摆角速度响应曲线（正弦转向工况）Fig.10 The yaw rate responses（sinusoidal steering）

图11 四轮轮胎纵向力（正弦转向工况）Fig.11 Four-wheel tire longitudinal forces（sinusoidal steering）

图12 四轮轮胎滑移率（正弦转向工况）Fig.12 Four-wheel tire slip rates（sinusoidal steering）

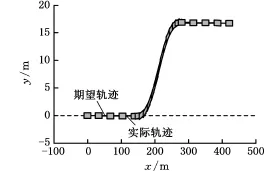
图13 车辆行驶轨迹（正弦转向工况）Fig.13 The vehicle desired and actual rajectories（sinusoidal steering）

从图9、图10中可以看出，在采取DYC控制和优化分配后，两种控制器的横摆角速度和质心侧偏角都能较好地跟踪理想模型。相较于DYC控制，本文优化分配下的车辆横摆角速度响应γo能更好地跟踪理想横摆角速度γd，车辆质心侧偏角βo也得到了很好抑制，显著小于DYC控制质心侧偏角βDYC，车辆能够很好地稳定变道。图11给出了四轮轮胎纵向力。图12为轮胎滑移率，开始变道后，滑移率迅速上升，但在滑移率控制器的作用下始终小于0.2。图13给出了车辆质心的期望轨迹、实际轨迹和航向，表明车辆能按理想轨迹完成变道行驶。

3.3 转向故障工况

图14 质心侧偏角响应曲线（转向故障工况）Fig.14 The centroid angle response（steering failure）

图15 横摆角速度响应曲线（转向故障工况）Fig.15 The yaw rate response（steering failure）

图16 前轮、后轮转向角曲线（转向故障工况）Fig.16 Front and rear wheel steering angles（steering failure）

图17 车辆行驶轨迹（转向故障工况）Fig.17 The vehicle desired and actual rajectories（steering failure）

正弦工况的仿真过程中，4s≤to＜5 s时设置前轮转向失效，5 s≤to≤6 s时后轮发生转向失效。图14～图17给出了转向故障工况的仿真结果。由图14可以看出，在转向失效的时间段，虽然质心侧偏角有较大波动但小于10°；图15中横摆角速度有一定的波动，但仍在车辆可控范围内。事实上在转向器发生故障后，控制策略需要在余下可用的执行器中重新计算并分配控制量，以适应新的控制环境。图16给出了前轮、后轮转向角，在图中的故障时段内，转向角调节失效并锁定。图17给出了车辆行驶轨迹。

3种工况下的仿真结果表明，所设计的控制系统能够很好地跟踪理想模型，保持车辆在高速转向、变道和转向故障等情况下的操纵稳定性，且系统响应迅速，具有很好的控制效果。

4 结论

本文建立了DEV车辆稳定性模型，根据各车轮转矩可以直接控制的特点，以质心侧偏角和横摆角速度为控制变量，设计了基于转矩协调的分层车辆稳定性控制方案。采用引入横摆角后的积分二自由度控制模型来计算期望横摆力矩，实现两控制变量的解耦，减小稳态跟踪误差；基于LQR方法进行控制量的优化分配，引入虚拟控制量，在不影响横摆角速度跟踪的情况下，放宽对质心侧偏角的约束。设计滑模滑移率控制器，实现定滑移率的车轮转矩控制。对汽车在高速转向和移线行驶的不同工况进行了仿真，结果表明控制系统能很好地跟踪横摆角速度的期望值，并保持质心侧偏角最小；当转向机构出现故障时，系统能有效重构并实现控制量再分配。该系统充分发挥了DEV的优点，有效地改善了汽车行驶的稳定性，提高了车辆安全性。