时间测度链上带有积分边界条件的二阶边值问题对称正解的存在性

王 静

（兰州文理学院 教育学院，甘肃 兰州 730000）

Hilger[1]首次提出了时间测度链上的分析理论,将看起来不相关联的连续分析和离散分析进行了高度统一.之后,测度链上动力方程的新理论在生物种群模型、神经网络、自动控制、医学动力学模型、经济学和社会科学领域中都有非常重要的应用[2].与此同时,测度链上的几类典型的动力方程边值问题的研究引起了学术界的广泛兴趣和高度关注,并得到了一些很好的结果[3-8].

本文考虑时间测度链上三点边值问题

其中,T表示对称时间测度链，α,β＞0,非负函数h1,h2∈L1([2,b])且在[a,b]上对称；f∈C([a,b]×[0,∞)×R→[0,∞)).

为了后面推理的需要，做如下记号：

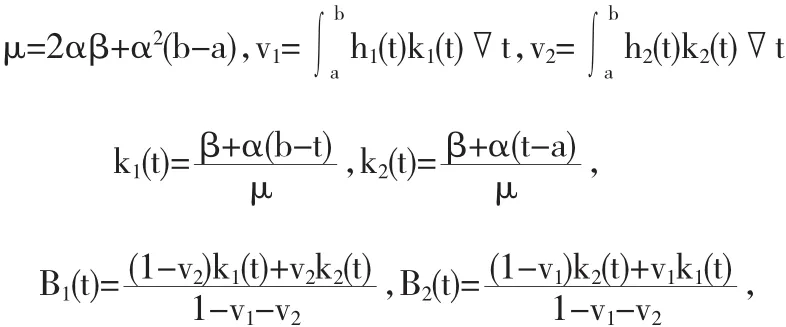
1 预备知识

定义1 对称时间测度链：∀t∈T，[a,b]⊂T，若b+a-t∈T，则称T为对称时间测度链.

定义2 时间测度链上对称函数：∀t∈T，若函数u:T→R且u(t)=u(b+a-t)，则称u为时间测度链[a,b]⊂T上的对称函数.

全文做如下假设：

(H1)α,β＞0；

(H2)非负函数 h1,h2∈L1([a,b])且在[a,b]上对称,1-v1-v2＜0；

(H3)f:[a,b]×[0,∞)×R→[0,∞)连续,f(·,u,v)在[a,b]上对称且 f(t,u,v)=f(t,u,-v)，(t,u,v)∈[a,b]×[0,∞)×R；

(H4)f(t,·,v)，f(t,u,·)为非减函数，(t,u,v)∈[a,b]×[0,∞)×R.

为了得到本文的主要结果,需要以下几个重要引理.

引理 1 设(H1)(H2)成立,μ≠0,p∈C([a,b]),方程

在边界条件(2)(3)情况下有唯一解，

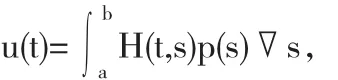
其中

证明 设u(t)是方程(4)的解.对(4)式进行积分,可得

再次积分,有

由边界条件，可得

因此,

且

即有

从而，可知

其中G(t,s)如式(6)所示.

考虑

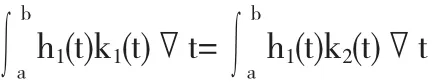
令h1(t)与式(7)相乘，并对其进行积分处理，可得

其中

类似,令h2(t)与式(7)相乘，并对其进行积分处理，可得

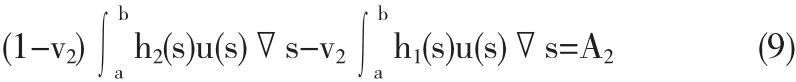
其中

由式(8)和(9),可得

即有

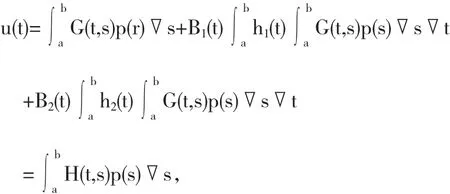
其中H(t,s)如式(5)给出.引理得证.

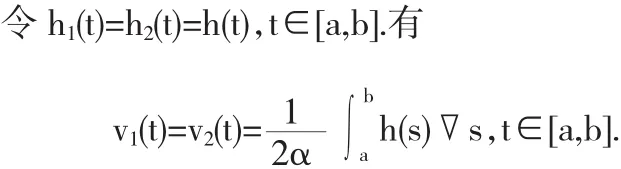
因此，(H2)可表述为：

(H2)h∈L1([a,b])非负，且在[a,b]上对称

在h1=h2=h情形下唯一解u(t)可表示为

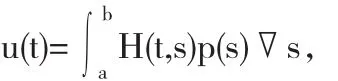
其中，

引理2 设(H1)(H2)成立，则有

证明 (i)显然成立.下证(ii)和(iii).

证明 (ii)设 t≤s，则 b+a-t≥b+a-s由式(7),可得

类似的,可证 G(b+a-t,b+a-s)=G(t,s)，s≤t.这样,有

由式(5),对 s,t∈[a,b],有

得证.

证明 (iii)若 t≤s，由式(7)和(H2),有

类似的,容易证得

再由式(6),可知

另外,当 s,t∈[a,b]，有

从而

因此,对当 s,t∈[a,b]，有

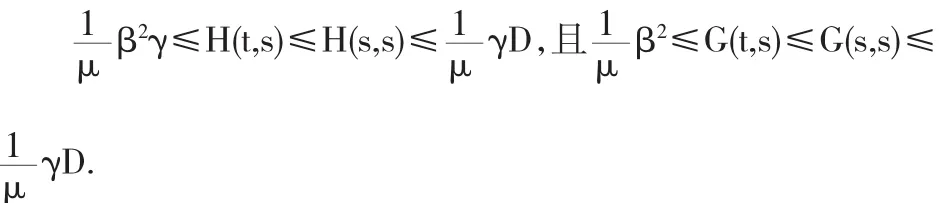
得证.

设 Banach 空间 E=C[a,b]且其范数为 ||u||=max{||u||∞,||uΔ||∞},其中定义锥 P⊂E,且 P={u∈E:u(t)≥0，u 是对称凸函数}.对于u∈P,S:P→E,定义

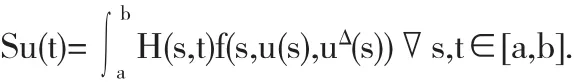
引理3 设(H1)(H2)成立，则S:P→P是全连续的且为非减函数.

2 主要结果

本文的主要结果及证明.

定理 1 设(H1)-(H4)成立.若存在两个正数a1,c且a1＜c使得

且

则问题(1)-(3)有唯一解w*∈P,且满足

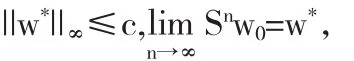
证明 分三步来证明.令Pc={w∈P:||w||≤c}.

第一步证明SPc⊆Pc.设w∈Pc,则有

由式(10)、(11)、(12)及引理 2 可知,

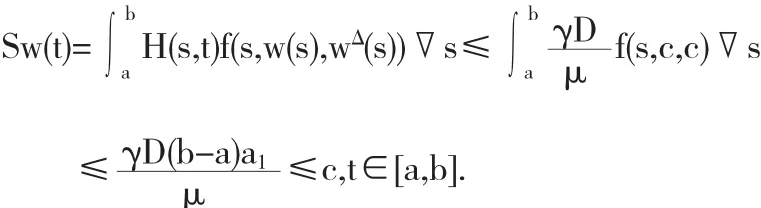
另外,由式(5),(6),(10),(11)及(12)可知,对于 t∈[a,b],有

因此可得 ||Sw||≤c,即

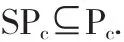
第二步证明 ||w0Δ||∞≤c，w0(t)∈Pc.设 w0(t)=(b-a)a1G(t,t)+，t∈[a,b],由式(11)和引理 2,易得 ||w0Δ||∞≤c.再由G(t,s)，可知

分两种情况讨论：

由式(13),(14)和(15),可得

第三步证明 Sw*=w*.设 w1(t)=Sw0(t),w1(t)∈Pc,wn+1=Swn=Sn+1w0,(n=0,1,2,…).由 SPc⊆Pc,可得 wn∈Pc,(n=1,2,3,…).由引理3,可知 S 是紧的.另设有收敛子列1,且存在 w*∈Pc,使得 wnk→w*.从而，由 S 的定义、引理 2 及式(10),可得

因此,有 w1(t)≤w0(t),t∈[a,b].从而,据引理 3,可知 Sw1(t)≤Sw0(t),t∈[a,b]，即 w2(t)≤w1(t),t∈[a,b].从而得

即得wn→w*.由 连续,可得

得证.