匀质三角薄板转动惯量的计算

叶 松，许明坤，张自锋

（巢湖学院 机械与电子工程学院，安徽 合肥 238000）

转动惯量是研究刚体运动所必需的基本物理量之一.匀质三角薄板是重要的平面结构，它可以和弓形等结构构成工程中常用的复杂刚体结构[1,2].由于转动惯量的可叠加性，讨论匀质三角薄板的转动惯量对分析复杂刚体结构的转动惯量非常有用.文献[3]给出匀质三角薄板对经过质心的任意转轴的转动惯量，但计算过程繁琐.文献[4-7]推导了三角形框刚体的转动惯量，但是该结论不能直接推广到匀质三角薄板刚体.在工程实践中平面刚体定轴转动的Z转轴一般都是垂直刚体平面，因此得到适用匀质三角薄板质心的转动惯量的简洁公式是有必要的.本文基于平行轴定理和垂直轴定理简捷地推导出匀质三角薄板刚体的质心转动惯量公式.

1 匀质三角薄板对坐标轴的转动惯量

已知垂直轴定理对给定Z轴的转动惯量与在薄刚体平面的X轴和Y轴选取无关.因此为了使讨论过程简洁，设匀质三角薄板底边AB在X轴，高OC在Y轴，顶点A、B和C的坐标如图1所示.

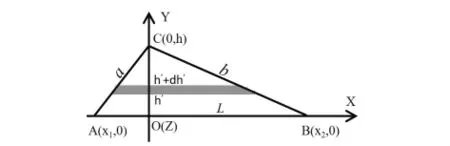
图1 计算匀质三角薄板对X轴转动惯量时的质量微元示意

首先讨论匀质三角薄板对X轴的转动惯量.取细杆微元位于[h',h'+dh']，长为L'，其对X轴的转动惯量微元是：

(1)式中σ是匀质三角薄板的面密度，其中：

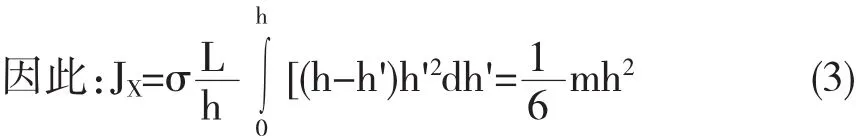
式(2)和(3)中L和h是AB和OC的长度.

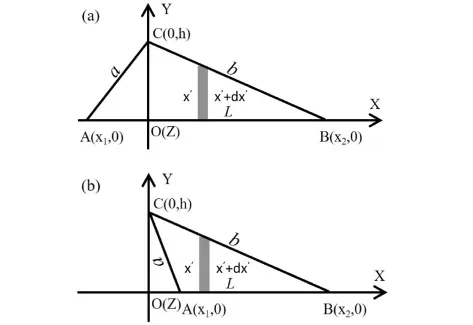
图2 计算匀质三角薄板对Y轴转动惯量时的质量微元示意

其次讨论匀质三角薄板对Y轴的转动惯量.如图2所示是匀质三角薄板的A、B顶点X轴坐标值满足x1x2≤0和x1x2＞0的两类情形.匀质三角薄板对Y轴的转动惯量，对图2(a)所示情形，等于△AOC和△BOC对Y轴的转动惯量之和；对图2(b)所示情形，等于△BOC和△AOC对Y轴的转动惯量之差.由公式（3）得到图2(a)和2(b)的转动惯量均为：

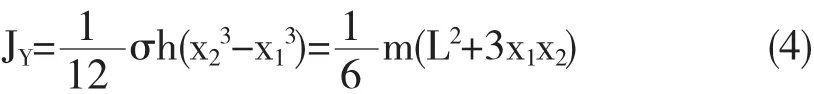
最后由垂直轴定理可以得到匀质三角薄板对Y轴的转动惯量：

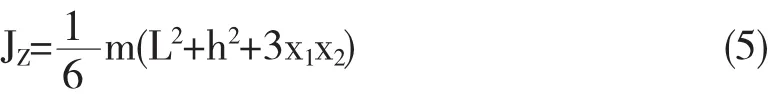
2 匀质三角薄板对质心的转动惯量

匀质三角薄板对质心的转动惯量可以运用平行轴定理计算.如图3所示，G是匀质三角薄板的质心，其坐标为和 GZ'是匀质三角薄板质心G的主轴，分别平行X轴、Y轴和Z轴.

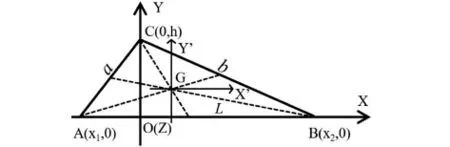
图3 计算匀质三角薄板过质心定轴转动惯量的示意

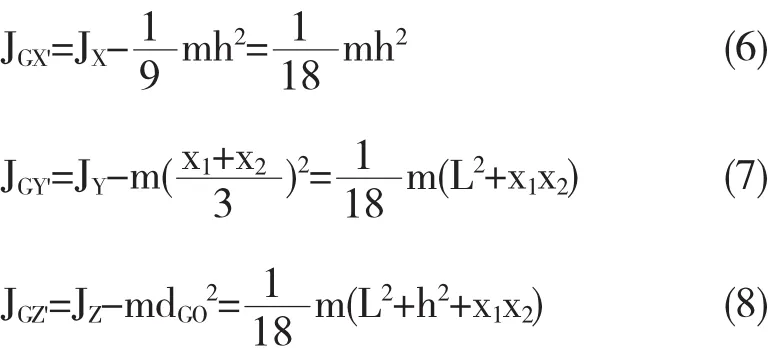
（8）式中是质心到坐标原点的距离.

在工程实践中，三角形刚体的边长是易于测量的，因此得到用边长表示的转动惯量是有必要的.记三角形边长分别为a、b、L，(6)-(8)式可以表示为：

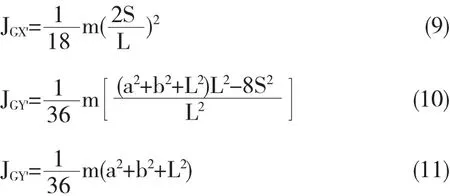
(9)式中

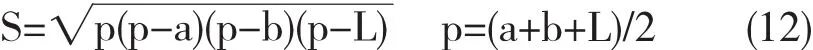
（11）式与文献[3]的推论一致.

3 结论

通过求解特定坐标系中匀质三角薄板对边长的转动惯量，结合平行轴定理和垂直轴定理，推导了匀质三角薄板对质心转动轴的转动惯量公式.求解思路清晰，过程简捷，有助于提高学生对平行轴定理和转动轴定理的理解和应用，对拓宽学生计算刚体转动惯量的数理思路有一定引导作用.