Origin软件在数学建模教学中的应用

李玉叶

（赤峰学院 数学与统计学院，内蒙古 赤峰 024000）

1 引言

数学建模是把数学知识与客观实际问题联系起来的纽带，是数学走向应用的必经之路,是培养学生综合素质特别是数学应用能力的重要途径[1,2].而《数学建模》这门课程是培养学生利用数学知识，基本理论和方法去分析、解决实际问题的能力.在解决问题的过程中，除了用到数学推理以外，通常还要处理大量数据，进行大量计算，这需要借助计算机，特别是在现代社会，要真正解决一个实际问题，离了计算机几乎是不行的.因此，《数学建模》课的教学中，计算机软件辅助教学是必不可少的，他们也起着越来越重要的作用.

在《数学建模》课的教学过程中，常用的计算机软件有Mathematica,Maple和Matlab等等，这些软件功能强大，可满足科技工作中的许多需要，但使用这些软件需要一定的计算机编程知识和矩阵知识，并熟悉其中大量的函数和命令，对于数学建模初学者存在较大难度.此外，这些软件所占内存大，移动起来比较困难.而Origin除轻便高巧，安装操作容易简单，安装包小，占用内存小等优点之外，使用Origin就像使用Excel和Word那样简单，只需点击鼠标，选择菜单命令就可以满足一般用户的需求，也可以满足高级用户数据分析、函数拟合的需要，是目前最为流行的数据分析软件之一.因此，开发Origin软件中的一些功能，将其应用于数学建模课堂教学，显得尤为重要.通过Origin的简便操作，使同学们快速掌握数学建模过程中一些函数、数据的图形化处理，使所考虑的问题生动，形象，直观地呈现出来，进而加深同学们对建模问题的理解.

2 Origin软件在教学中的使用

本文以Origin软件在《数学建模》教学中使用的几个教学实例.使用数学建模教材为姜启源等编的《数学模型》第四版[3]，以下都简称“教材”.

2.1 Origin软件在数学建模结果图形化中的应用

根据题意，求得λ=0.1386和μ=0.1155，进而得到肠胃中的药量x(t)和血液系统中的药量y(t)随时间的变化方程为：

孩子2小时候送到医院，若使用口服活性炭来吸附药物进行施救，即排放率μ增加为原来的2倍，即μ=0.2310，此时血液中的药量记为z(t)，可得随时间变化的方程为：

若采用体外血液透析的办法施救，药物的排除率μ可增加到原来的6倍即0.6930，此时血液系统中的药量即为g(t)，可得随时间变化的方程为

如果我们不借助软件使函数x(t)、y(t)、z(t)和g(t)可视化，同学们不易理解血液中药量的变化以及口服活性炭和采取血液体外透析之后血液中药量的变化.现使用Origin软件对(3)-(6)式作图，打开 Origin 软件，在工作栏“book”有两列，首先在空白处，点击右键“add new column”加列，使工作栏“book”中有五列，分别为 A、B、C、D、E 列，其次选中“A 列”，点击右键，再点击“set column value”在对话框里输入“i*0.1-0.1”,对话框里的“row”选择从 1 到 250，点击“OK”，这样我们就建立了从0到25，间隔0.1的时间序列t，如图1所示.再次，我们分别对B、C、D、E列建立关于时间t的函数x(t)、y(t)、z(t)和 g(t)，这里以 x(t)为例说明，选中 B 列，点击右键，再点击“set column value”在对话框里输入“1100*exp(-0.1386*A)”，点击“OK”，得到关于时间 t的函数 x(t)，如图2 所示.最后，点击菜单键“plot”选“line”，出现 plot setup 窗口，然后选A列作为x轴，B列作为y轴（如图3所示），再顺序点击“add”和“OK”，得到肠胃中的药量x(t)与时间t的函数图，如图4所示.其他的函数y(t)、z(t)和g(t)关于时间的t得序列图也是类似操作，函数 x(t)、y(t)、z(t)和 g(t)关于时间 t总图，如图5所示.

图5可知，孩子在到达医院时已经出现严重中毒，即血液中的药量y(t),在约2h达到200mg，若不及时施救，约在5h后出现致命情况，即药量y(t)将在约5h达到400mg.就医后，若采用口服活性炭的方法施救，在到达医院约3h后，药

图1 建立时间t序列

图2 建立x(t)序列

图3 选取t序列为X轴，x(t)序列为Y轴

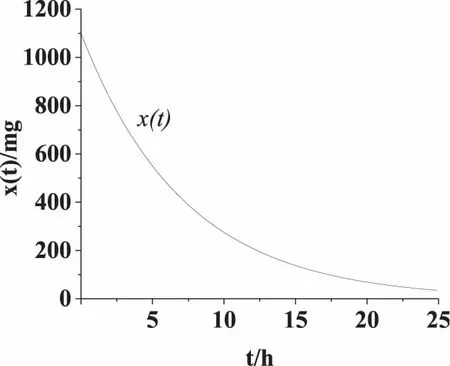
图4 肠胃中的药量x(t)与时间t的关系图

图5 函数 x(t)、y(t)、z(t)和 g(t)时间 t的关系图

现对1970年到2000年的美国人口（如表1所示）使用Origin进行分析和预测.

为了估计指数增长模型（7）或（8）中的参数r和x0，需将（8）式取对数，得

以美国人口数据为例（见表1），通过(9)式用1790年至1900年的数据（美国人口的部分数据），进行Origin拟合，首先打开Origin软件，然后把美国数据分别按年和人口数建量z(t)达到最大，低于400mg，即脱离致命情况；若采用体外血液透析的方法施救，在施救后g(t)（t≥2）立即下降，病人不仅脱离了危险而且很快得到缓解.对于没有学过任何软件的同学，经过讲解都很容易上手，另外操作过程是直观化的进一步加深了对问题的理解.

2.2 Origin软件在数学建模数据分析与拟合中的应用

表1 美国人口[3]

图6 对1790年至1900年的美国人口进行线性拟合

图7 对1790年至1900年的美国人口进行线性拟合结果

图8 对1790年至2000年的美国人口进行线性拟合结果

从图7可以得出：斜率为0.2743，即得到r= 0.2743/(10 年)，截距为 1.43233，即 a=1.43233，从而 x0=lna=4.1884，因此得到拟合直线为y=0.2743t+ 1.43233；同样的方法可对全部数据进行拟合，得到拟合结果，如图8所示，斜率为0.2019，可得r=0.2019/（10年），截距为1.79923，x0=lna=0.587358，拟合直线为y=0.2019t+0.587358.然后对部分数据和全部数分别画散点图对拟合直线画函数图（Origin作图与图3类似），分别如图9(a)和9(b)所示.

通过图9(a)和9(b)展示同学们很容易理解：指数增长模型，用它作短期人口预测可以得到较好的结果，如图9(a)所示；但是从长期来看，指数模型不能描述也不能预测较长时期的人口演变过程（图9(b)所示），这是因为任何地区的人口都不可能无限增长的，与现实相符.对于数学拟合这块比较难于理解，通过Origin软件的简易操作即作图展示，加深了同学们的指数增长模型的理解.

图9 散点图和拟合曲线

3 结束语

在《数学建模》课上应用Origin软件辅助教学给学生带来了浅显、直观的视觉效果是显而易见的.在数据暴增的信息时代，对于用数学建模解决实际问题的我们，不但需要掌握所建模问题的知识背景，更需要综合数据分析软件的支持.在数学建模的科研和教学过程中，本文阐述Origin软件在数学建模中的具体应用，不仅能够提升建模的效率，而且能够丰富其手段和方式，并推进了Origin软件的深化推广和应用.今后可根据Origin软件有内置的数据传递功能，进一步开发Origin数据处理的在《数学建模》的教学中应用，可以采取联合使用软件，实现MATLAB数据处理与Origin科技绘图的优势互补和内部融合，在满足现有教学条件的基础上，针对学生的实际状况，深度挖掘数学建模课的内涵与外延，通过Origin数据处理的应用，并与其他软件的融合，进一步提升对数学建模课的认识.