基于贪婪算法的拍照定价问题的计量分析

王 婷，朱 磊，张月蕾，贡杨泰

（1.安徽财经大学 金融学院；2.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030）

“拍照赚钱”是移动互联网下的一种自助式服务模式.这种基于移动互联网的自助式劳务众包平台，为企业提供各种商业检查和信息搜集，相比传统的市场调查方式可以大大节省调查成本，而且有效地保证了调查数据真实性，缩短了调查的周期.App成为该平台运行的核心，而App中的任务定价又是其核心要素.因此本文主要通过贪婪算法模型，对原来定价进行修正后并制定新的定价方案，为任务发布者以及实行者提供合理的参考依据.

1 数据来源与模型假设

本文做出以下模型的假设：⑴假设会员在执行任务时，选择任务时是理性的，优先选择离自己近的，价格高的任务.⑵假设会员的定位是会员自身的位置定位，而不是居住的IP定位.⑶假设会员获得任务的渠道是一致的，不存在时间上的延迟.

2 任务未完成原因分析

2.1 研究思路

首先将地图无忧所收集已结束项目的任务位置数据在地图上可视化，通过观察地图上任务完成分布情况，结合会员信息分布情况，然后将任务完成分布情况分成四类，找到聚类中心点[2]，在不同类中将已完成任务与任务标价进行相关性进行分析，进行分区，找出定价规律.最后通过经纬度转换找出分布情况，通过分析任务完成情况所在位置，结合任务定价和会员属性，分析得出任务未被完成的原因.

2.2 研究方法

将已结束项目的任务位置信息利用R语言可视化，将完成任务和未完成任务和会员聚集情况[3]同时将任务定位导入到地图无忧中，分别得到图1、2.

结合图1、2进行分析，得到如下现象：大部分会员聚集的地方，任务完成度较高，但是仍存在会员很少但任务却完成；会员离任务很近，但任务却未被完成；某一区会员众多，却存在任务未被完成的情况.因此可能存在定价问题.针对所挖掘的信息，建立出聚类分析模型，研究定价规律和未完成的原因.

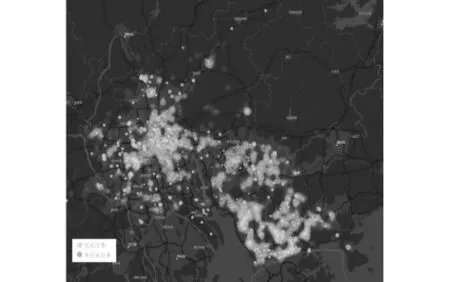
图1 任务完成情况热力图

图2 任务在地图上可视化

2.3 结果分析

对任务的位置进行聚类分析，观察图2，可以发现任务完成情况存在明显的分区现象.因此选择软件进行K-mean将其分为四类将任务经纬度数据导入MATLAB中进行处理得到四个中心点位置分别为:(23.014861,113.184759）；（22.663103,114.046420）；(23.278157,113.326456)；（22.956052,113.749090）.

利用EXCEL表对全部任务经纬度进行转换成距离.为进一步求解出任务完成度和会员的关系，利用转换出的距离本文等分成大小相同的正方形，将数据置于网格化量化得到图3.

图3 会员信息网格化

图例说明格网颜色代表会员人数，红色越深代表人数越少，越偏向黑色代表人数越多，格网的数字右下角黄色标签表示该网内会员数，左下角绿色代表完成任务人数，左上角白色标签代表未完成的任务的人数.根据图中所反应的信息，虽然会员分布在较多黑格子中，但是任务完成度并不乐观，白色标签未完成的任务大部分分布在灰色盒子中.任务未被完成的原因可能由于定价偏低，影响会员积极性.

结合图1、2、3行比较分析，发现不同区任务完成分布不同，同时不同区域的定价和中心点的距离，存在不同的变化关系.因此必须进行分区计算定价和距离的相关系数，分析两者之间的相关关系.

令对已完成项目任务数据中各区相关系数分别为：ρ1；ρ2；ρ3；ρ4.

通过分区进行相关性分析，不同区的相关性还是存在明显差异，这与其经济发展情况密切相关，由于不同地区经济发展情况不同，会员对任务定价接受程度不同，可能即使存在任务，也不愿接单.

2.3.1 任务定价规律：针对不同区，任务定价存在差异，从图中可以看出，部分偏离中心点很远处，定价比较高.可能是为了鼓励更多人注册会员；在会员集中的地方，任务定价偏低；但是由于存在限制单数的情况，因此在集中的区域也会有未完成的任务；由于经济环境的差异，商家所给出的价格并不能满足参与者所接受的价格，因此可能存在任务无法完成的情况.

2.3.2 任务未完成的原因:任务与会员距离太远，成本太高；部分地区会员数太少，不能与任务达到供需平衡；任务所给出的定价，不能满足参与者的需求；预定任务开始时间的间断性，使得部分任务无法完成；会员预定任务限额，使会员集中区也可能存在任务无法完成的情况.

3 任务定价方案

3.1 研究思路

对项目设计新的定价方案，分3个步骤，第一步根据会员信息中的每个会员的信誉值估计出他们完成任务的质量；第二步根据那些区域附近已完成任务的定价估计会员完成任务所需的成本和每个会员预定任务的限额，对任务进行定价；第三步根据会员完成任务的质量（对信誉值处理）进行降序排序，采用贪婪算法[4]进行任务分配，再通过类比推理得出定价范围.

3.2 研究方法

发布者通过自助式劳务众包平台发布任务，并进行定价.但影响定价的因素有很多，在这里主要考虑会员本身因素[5]（完成任务的质量、成本、最大完成任务数量）、会员密度、任务密度、区域经济发展水平.根据已完成项目任务的经度、纬度数据，得出任务分布在4个地级市，具体到区（或者县级市、县）共有25个区域.经过EXCEL筛选得到不同区域任务完成度（见表1）.

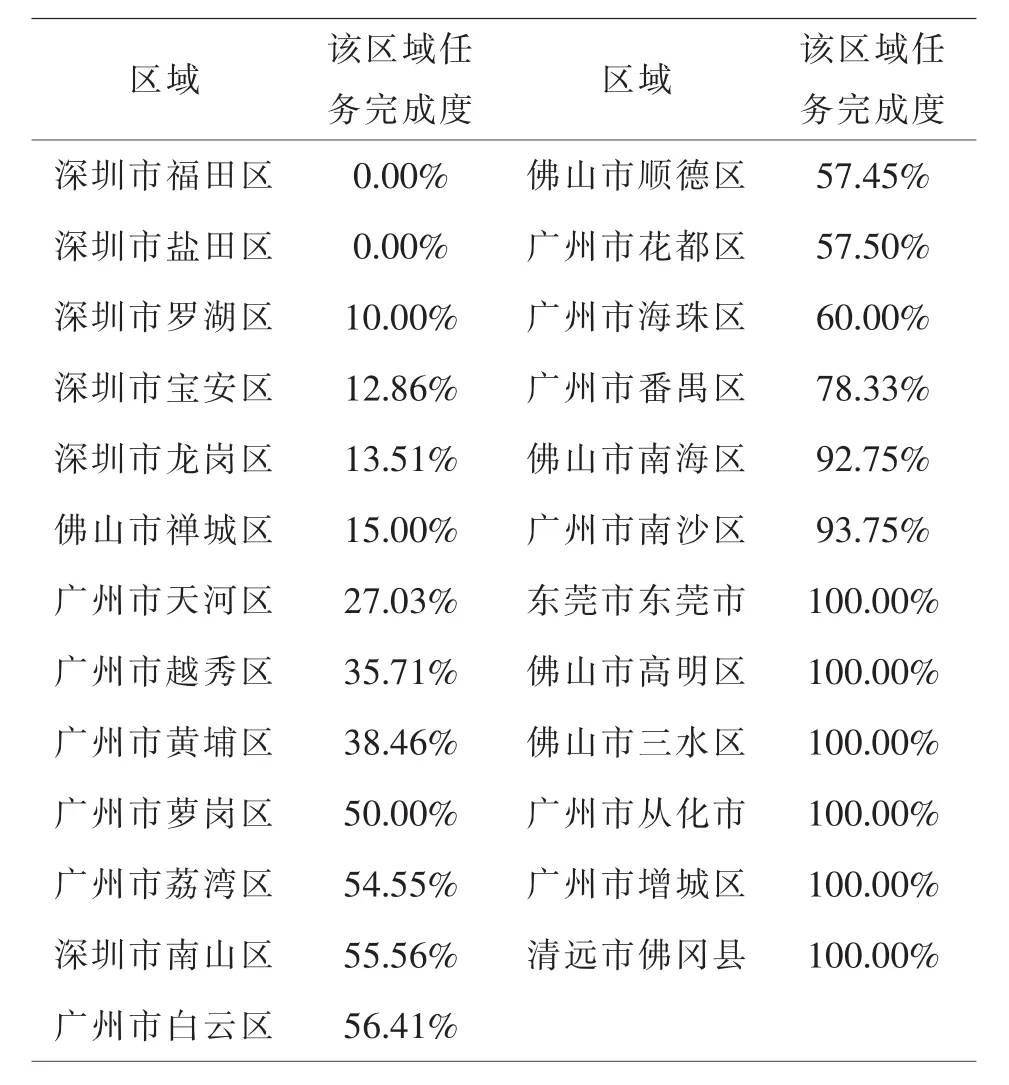
表1 不同区域任务完成度

佛山市南海区、广州市南沙区、东莞市东莞市、佛山市高明区、佛山市三水区、广州市从化市、广州市增城市、清远市佛冈县任务完成情况均达到92%以上，说明这些地区定价结构比较合理，只需考虑其他地区的定价方案即可.

有界贪婪算法[6]:

（1）选取区域内部分会员，取得“任务预算（即某个会员能够完成的最大任务个数及位置范围）”Bp=εB，设置t=1（2）在情况下重复以下步骤.（3）给会员分配任务.（4）.（5）结束当前步骤.（6）结束当前循环.（7）对会员按照ci进行升序排序.（8）在最后一轮中，重复以下步骤.（9）判断剩余“任务预算”BP＜minci.（10）如果成立跳出循环.（11）否则，选择剩余会员中符合条件的会员.（12）BP=BP-ci.（13）结束当前步骤.（14）结束当前循环.（15）对会员进行完成任务质量估值：多次探索取平均值的方法.（16）根据上一步骤得出的结果，得出函数：μi=f(ci).（17）利用函数得到剩余会员的任务质量估值.（18）算法结束.

通过C++贪婪算法编程，求得区域会员与任务的一种对应关系.

深圳市福田区任务完成度0%，由表2知，该区域的任务标价较低，然而该区域内会员数量较多，因此应合理地提高任务价格.同理也可以分析得出：广州增城区、南沙区和佛山市三水区的任务定价均较高，但是这些区域任务位置离会员平均距离较远，因此对定价也有影响.

综上知，以深圳市福田区、广州市天河区等17个区（除佛山市南海区、广州市南沙区、东莞市东莞市、佛山市高明区、佛山市三水区、广州市从化市、广州市增城区、清远市佛冈县之外），应适当提高定价，在考虑其他地区会员位置与任务位置的关系后，觉得将这些地区的任务定价范围确定在70～75.

4 基于距离范围确定的完成度模型

4.1 研究思路

把任务联合在一起打包发布[7]，对任务点进行筛选后，再对会员的经纬度聚类分析.最后以贪婪算法定价模型为基础进行扩展得出任务分配及其完成情况的变化，并且分析任务完成率的高低变化情况.

4.2 研究方法

首先筛选出信誉度较高且任务限额大于10的会员，得出符合要求的会员共有252个；接着根据市场的供求关系，并且结合图1和图3分析任务与会员的大致位置后，将任务位置通过MATLAB聚类分析得到252个“联合任务”的位置.

任务发布者往往追求任务能够全部完成，因此本文将“联合任务”与会员一一对应，以期望得到任务完成度最大，但现实情况中有些任务离会员较远，对已完成项目任务的数据进行处理，计算出原始数据中的任务完成情况，通过统计完成任务个数与总任务个数对比得到任务的完成率：

其中q为任务完成情况，Xi表示任务完成的个数，Xn表示为总的任务个数.

对于打包分布情况下数据处理——经纬度转化为距离，根据欧氏距离公式：

考虑到任务个数和会员个数较多，将两组数据导入Excel软件中，选择出所有中的最短距离.

4.3 结果分析

通过App软件数据分析可以得到，一般在距离在3000米以内的任务几乎都被实行，在3000米之外除了现实中一些偶然因素，一般情况下任务都没有得得到完成.这恰好与图表中的呈现的会员与任务点集聚分布相似相符.根据所搜集到的数据，统计出任务点与会员点之间的距离在3000米以内的个数为200，因此方案的完成率为P=200/252=79.365%

通过对于打包分布情况下任务完成率与不打包分布的情况下的任务完成率对比可以发现，在对任务进行打包后得到的任务完成率有所提高，减少了由于用户互相选择出现了任务无人选择的情况.

5 分区拟合回归模型

5.1 研究思路

本文选取已完成任务的定价价格、经度、纬度会员密度、会员信誉度作为指标，进行回归拟合[8].

5.2 研究方法

将新项目任务数据导入到地图进行可视化分析，得到图4.

图4 任务分布位置图

可以观察到待处理数据大部分分布在广州市，还有零散的点分布在深圳市及附近.因此分区进行处理.由于前面的分析结论，得知虽然深圳市会员密度高，但是会员活跃度不高.由于经济发展水平不同，导致定价水平存在差异.因此本文首先对广州市进行回归拟合分析，然后将深圳市及附近的数据通过类比前面已建立的模型，进行定价.由于并没有搜集到会员所完成的具体任务，因此将会员信誉度作为虚拟变量引入.

经过几个函数的拟合优度、模型显著性进行对比，本文选取拟合优度最好，模型通过显著性检验的数据.通过Stata进行回归拟合，Y代表任务定价、C代表经度，V代表纬度、M代表会员密度、ξ代表随机干扰项得到如下模型：

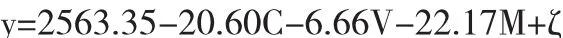
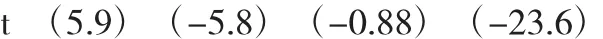
各个t值所对应的p值均小于0.05，拒绝原假设，各变量显著.同时F(3,125)=13.45，模型显著.R2=0.875，模型拟合优度较高.

将广州区已经完成的任务，利用EXCEL将数据带入回归方程，通过计算预测值和实际定价的差值，用STATA做出误差散点图，如图5所示.

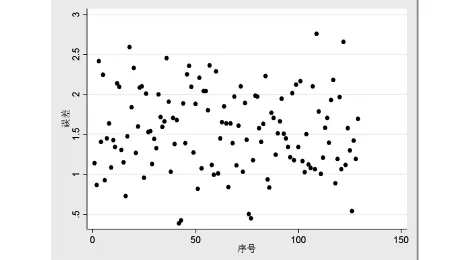
图5 误差散点图

根据图5可以看出误差大部分分布在0-3中，误差范围并不大，在实际情况实行中，误差可能来自会员信誉度，可以根据任务发布点，会员信誉情况引入虚拟变量Di,根据会员信息中的信誉值，将信誉值进行分段：

极差=Max信誉-Min信誉，采用等距分组，将区间分为：

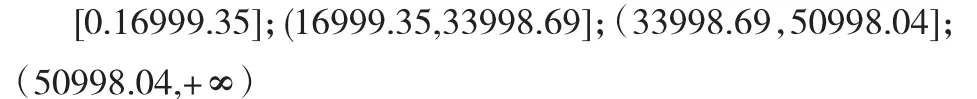
将虚拟变量赋值为0.75；1.5；2.25；3，并且引入回归函数中，其中bi表示接受任务会员的信誉水平：

经过广州市已完成任务误差散点图分析，证明模型可行性较好，加入有关会员信誉的虚拟变量，回归函数针对位于广州市地区的任务做出了较为准确的定价方案.根据新方案中所给的经纬度信息，将所处广州市的经度、纬度、会员密度一一对应，便可求出所求定价.

5.3 结果分析

已经看到深圳任务完成度在15%以下，但是在地图上深圳所在地区会员数量并不低.针对此现象，本文将数据利用R语言进行可视化，得到会员与完成任务的叠加图如图6，会员与未完成任务叠加图如图7所示.

结合图6针对深圳市宝安区，即图6中深圳市左下角处，黄色点较小，完成任务的定价处于[65,67]，因此进行定价，同时为了调动会员的积极性，可以对价格进行正方向的微调.同时在深圳市右上方红色集中区，对比之前会员完成图注：黄色点代表未完成的会员叠加，红色点代表完成任务，点越大标价越高，格网代表会员数，红色人少，黑灰色人多.情况定价，黄色点较大，价格普遍在[76,80]之间.

图6 任务完成叠加图

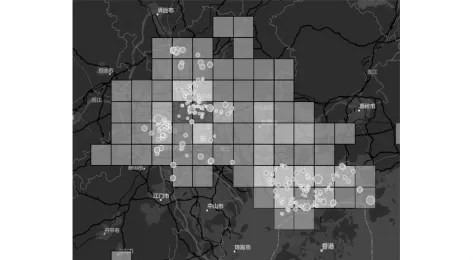
图7 未完成任务叠加图

6 结束语

本文的特色是运用R语言强大的视图功能，结合多种统计软件，使复杂的问题借助图形得到较为准确和完整的结果,以深圳市福田区、广州市天河区等17个区价格作为参考依据，在考虑其他地区会员位置与任务位置的关系后，觉得将这些地区的任务定价范围确定在70～75.