关于图与线图的距离指标关系问题研究

朱 娜盛兴平

（1.安徽理工大学 数学与大数据学院，安徽 淮南 232001；2.阜阳师范学院 数学与统计学院，安徽 阜阳 236037）

0 引言

本文中所有的图都是有限的,简单的,无向的.对于一个图G，分别用V（G）和E（G）表示它的顶点集和边集。G的一条途径是指一个有限非空序列W＝v0e1v1e2v2…ekvk（0≤i≤k），它的项交替地为顶点和边，ei的端点是vi-1和vi，称W是从v0到vk的一条途径，，v0和vk分别称为W的起点和终点。若途径W的边e1，e2，…，ek互不相同，则W称为迹。又若途径W的顶点v0，v1，…vk也不相同，则W称为路。路Pn=v0，v1，…vn表示顶点分别为v0，v1，…vn的路.如果迹的起点和终点相同，则称为闭迹。若一条闭迹的起点和内部顶点互不相同，则称它为圈。[1]一个长为n的圈记作Cn。如果V(H)U V(G)，E(H)U E(G)，并且ΦH是ΦG在E（H）上的限制，就称H是G的子图。假设V'是V的一个非空子集，以V'为顶点集，以两端点均在V'中的边的全体为边集所组成的子图，称为G的由V'导出的子图。

给定一个图G，它的线图L（G）满足：V（L（G））＝E（ G），e1e2∈E（ L（ G）），当且仅当e1与e2在G中有公共点。对于v∈V（G），记dG（v）是v在G中的度，简记为d（v）。用δ（GV）表示G的顶点的最小度。对于v，u∈V（G），dG（u，v）（或者用d（u，v）） 表示在G中u和v之间最短路的长度。对于e1e2∈E（G），定义dG（e1，e2）＝dL（G）（e1，e2）。W（G）指数是一个描述分子结构的不变量，是化学图论中最经典的分子拓扑指数之一，它可以用于设计具有理想性质的分子[2]。A.A.Dobrynin等人在2001年给出了树的W（G）指数[3].A.A.Dobrynin等人在2002年给出了W（G）指数关于六角形系统的结果[4]。近些年，很多人对图的W（G）指数和其线图的W（L（G））指数的关系非常感兴趣，尤其对于一个什么样的图满足W（G）＝W（L（G））做了很多研究。Nathann Cohen等人在2009年给出了对于每一个非负整数g0存在g＞g0，当图G的围长为g时，有很多图G满足W（G）＝W（L（G））[5]。罗宇等人在2014年定义了一类具有圈数为r，围长为n的平面图Gr，s，t，n并证明了对于满足特定条件的正整数r，s，t，n，存在无穷个这样的图Gr，s，t，n满足性质W（ Gr，s，t，n）＝W（ L（Gr，s，t，n））[6]。关于W（ G ）指数的详细内容和结果参见[7-12]。本文中的S（G）是W（G）在定义上的简单推广。记S（G）为图G的所有顶点对之间的距离的平方和，即S（G）＝本文主要研究路，圈以及最小度数为2的图G和其线图的L（G）顶点对之间的距离的平方和的大小关系。

1 路和圈的结论

本部分首先研究路Pn和圈Cn与其对应的线图L（Pn）和L（Cn）的顶点对之间的距离平方和的大小关系。

定理1：对于任意一条路Pn，则有S（ L（Pn））

证明：用数学归纳法证明。对于n＝2，等式左边等于S（ L（ Pn））＝ 0，等式右边等于S（ Pn）－＝12-1＝0，左边等于右边，所以这个公式在n＝2时成立。

考虑完路的情况，下面我们再考虑圈，由于对任意 Cn，Cn与L（Cn）同构，故显然有以下定理。

定理2：对于圈Cn，则有S（L（ Cn））＝S（Cn）。

对于双圈图的S（G）和S（L（G））的大小关系，没有一般性的结论，下面举例说明.双圈图G1，G2，G3如图1～图3所示，有S（ G1）＝ 204，S（ L（ G1））＝ 173，S（ G2）＝ 60，S（ L（ G2））＝ 60，S（ G3）＝ 22，S（ L（ G3））＝ 35 则S（ G1）＞S（ L（ G1）），S（ G2）＝S（ L（ G2）），S（ G3）＜S（ L（ G3））。

由上面的例子可以看出双圈图中有S（G）＞S（L（G）），S（G）＝S（L（G））和S（G）＜S（L（G））。

图1 G1

图2 G2

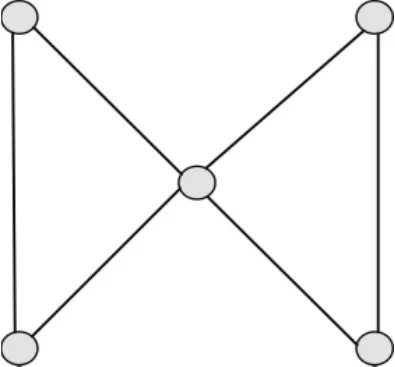
图3 G3

2 最小度至少为2的图的结论

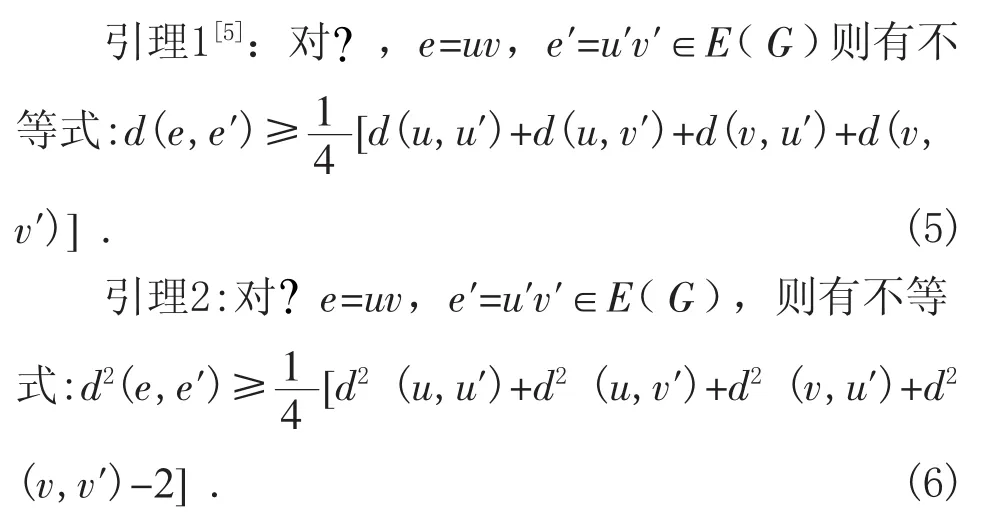
证明:假定d(v,v')=min{d(u,u')，d(u,v')，d(v,u')，d(v,v')}，可以得到

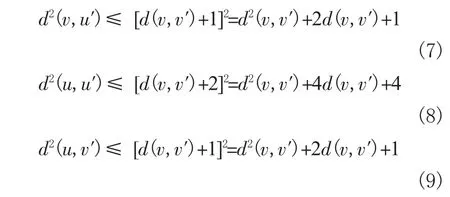
因此由(7)，(8)和(9)得到

定理3:G是连通图且δ(G)≥ 2，S(G)＜S(L(G))，当G是圈时等式成立.证明:如果G是圈，根据定理2等号成立.

因此，我们可以假定G至少有一个顶点的度至少3.通过引理2，我们有

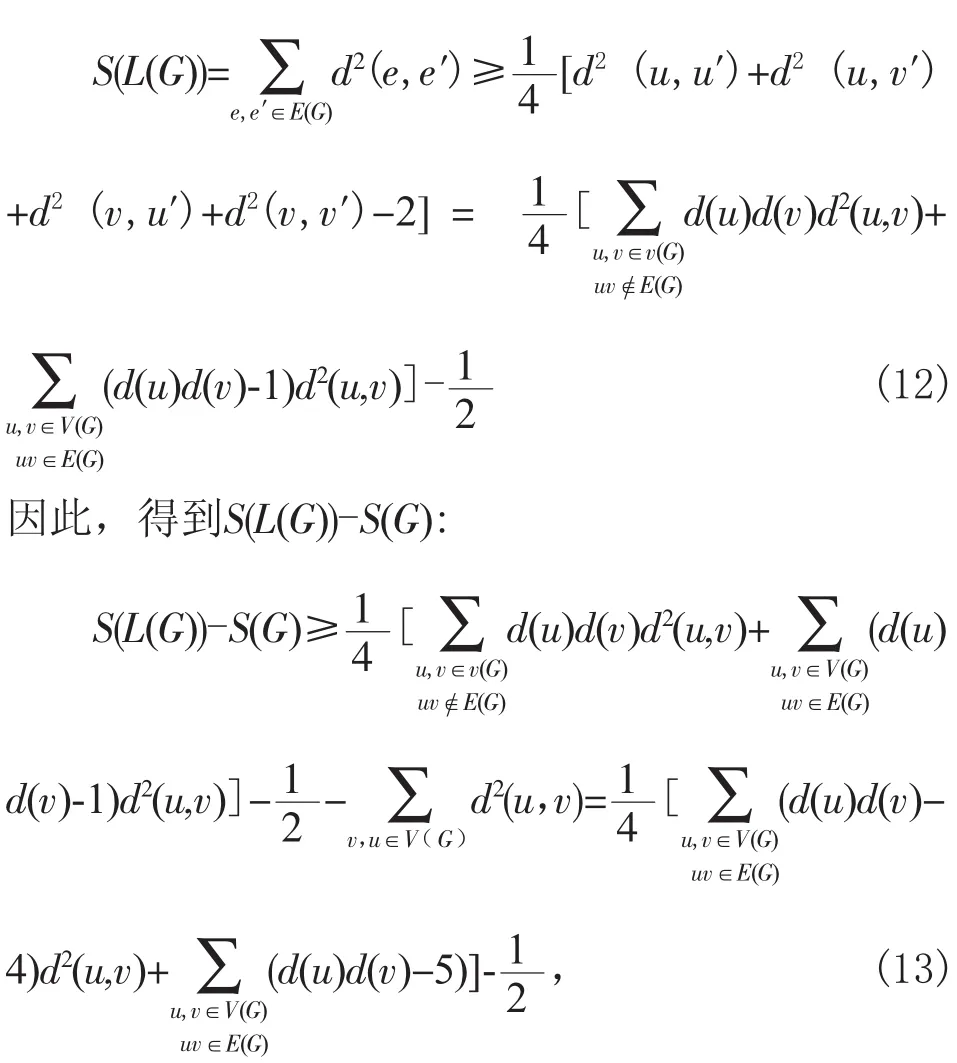
令G2为G中二度顶点的导出子图

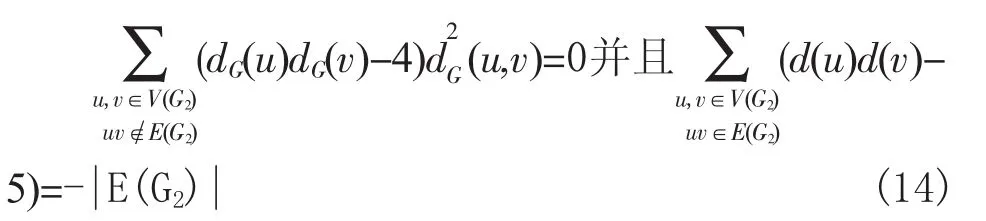
由(13)和(14)得到