基于递进复合式组合预测模型的软岩隧道大变形预测研究

赵淑敏

(陕西铁路工程职业技术学院， 陕西 渭南 714000)

0 引言

随着我国公路建设的快速发展，隧道大变形已成为常见的施工灾害[1]，对安全施工造成了较大的隐患。对其变形预测，能有效指导现场的变形预警和施工优化，研究意义明显。隧道大变形是由多种因素共同作用造成的，内因和外因都不可或缺[2]。在大变形的研究方面： 骆文学[3]采用有限差分的数值模拟对隧道大变形特征进行分析，得到软弱破碎带地质环境大变形规律，为该地质条件下的支护设计提供了参考。在隧道的变形预测方面： 李晓龙等[4-5]利用最小二乘法优化的支持向量机模型进行预测，得出最小二乘法对支持向量机的参数优化效果较为明显，提高了支持向量机的预测性能，预测效果较好； 黄志波等[6]将BP神经网络引入到大断面隧道的变形预测中，通过实例验证该方法的预测精度能满足工程需要，对现场施工能进行有效的指导； 谢齐等[7]和赖祖龙等[8]将灰色模型和BP神经网络进行结合建模，得出的预测结果与实测值间的差异较小，预测精度较高，适用性较强。但以上多是采用单一模型进行预测，且缺少在隧道大变形方面的预测研究； 同时，变质岩隧道具有其特有的地质条件，也缺少相应的变形预测研究。该文以支持向量机、灰色模型为基础，采用最小二乘法对2种方法进行参数优化，确定2种单项预测模型； 其次，以误差平方和为评价指标，确定组合权值，实现组合预测，并利用BP神经网络修正组合预测误差，以进一步提高预测精度。该文旨在通过2阶段递进预测，构建隧道大变形的二阶复合式预测模型，以期提高预测精度，并结合实例来探讨该模型的适用性和有效性。

1 基本原理

基于LS-SVM、优化GM(1,1)和BP神经网络的二阶复合组合预测模型的预测流程如图1所示。该模型的基本思路是： 充分发挥各参与模型的优势，将预测风险最小化，以增加预测模型的精度及稳定性，即首先利用LS-SVM和优化GM(1,1)模型对隧道变形监测数据进行预测，并采用误差平方和倒数法将两者的预测结果进行组合； 再进一步利用BP神经网络对两者的组合结果进行误差修正，以进一步提高预测精度，进而综合建立变质岩隧道的二阶复合式组合预测模型。

图1 二阶复合组合预测模型

结合本文工程实例，二阶复合式组合预测模型的预测步骤分述如下。

1)利用LS-SVM和优化GM(1,1)模型对隧道的拱顶沉降变形进行预测，并对比优化前后预测结果的差异，以探讨优化方法的有效性； 同时，以误差平方和为评价指标，确定组合权值，对两预测模型的预测结果进行组合。误差平方和及权值计算公式如式(1)和式(2)所示。

(1)

(2)

式中：wi为第i种方法的组合权值； SSEi为第i种方法的误差平方和；m为单项预测方法的个数。

2)利用BP神经网络对前者预测结果进行误差修正，以进一步提高预测精度，达到综合预测的目的，进而得到隧道拱顶沉降的变形预测值。

3)将本文预测模型再应用到隧道的周边收敛变形预测中，以检验本文预测模型的有效性，且通过对比隧道拱顶及周边的预测结果，对隧道后期的变形趋势进行分析，为现场施工提供依据。

1.1 支持向量机模型

支持向量机的学习方法及识别模式均是由统计学理论发展而来，采用结构风险最小化的原则，具有很好的泛化能力，对小样本也能实现很好的非线性预测[9-11]。

若隧道变形的样本表示为{xi,yi}，通过非线性映射将x映射到高维空间，进而构建出线性回归函数

f(x)=ωφ(x)+b。

(3)

式中：f(x)为回归表达式；φ(x)为非线性映射函数；ω为权重惯量；b为偏置量。

基于风险最小化原则，在超出ε条件下，引入松弛变量ξi、ξi*(ξi≥0、ξi*≥0)，则可将上述回归映射问题转变为：

(4)

(5)

式(4)和式(5)中：L(x)为Lagrange函数；b为偏置量；l为训练样本数；ω为权重惯量；ε为不敏感损失函数(将其设定为0.6)；C为惩罚因子。

根据对偶理论，将式(4)的优化问题转变为二次规划问题对偶问题，即：

(6)

(7)

式中：αi、αi*为拉格朗乘子；K(xi,yj)为核函数。

通过对式(6)的最终求解，可以得到回归函数

(8)

式中： 偏置量由KTT条件求得，且αi-αi*≠0为对应xi的支持向量。

核函数、核参数及正则化参数对支持向量机模型的预测性能具有较大影响，而上述参数又是由模型设计者设定，具有较大的主观性，对使用者的经验要求较高。因此，本文引入最小二乘法对支持向量机的参数进行优化，实现原模型由不等式约束到等式约束的转变，进而降低求解难度。结合实例特点，将优化过程分述如下。

1)支持向量机的核函数有3种，即径向基核函数、多项式核函数及线性核函数，其中，径向基核函数的非线性预测能力相对更强[12]，能有效解决复杂的非线性问题，故将其作为本文支持向量机模型的核函数。

2)通过网格化划分，对核参数及正则化参数进行网格取值，并利用最小二乘法采用交叉验证的手段筛选出最优参数组合。通过最小二乘法对参数的优化能有效避免多解性问题，得到最优的互偶解，且将两参数的优化区间均设定为[0,1010]，网格点数为1010×1010，步长均为1。

3)将最小二乘法优化得到参数带入到支持向量机模型中，建立优化支持向量机模型。在寻优之初，将核参数及正则化参数分别初始设定为0和1，经过寻优，得到最优核参数为51，最优正则化参数为 4 152 637。

1.2 灰色模型

灰色模型是基于模糊理论发展而来的，通过对少量或不完全信息的收集达到对事物发展规律进行长期预测的目的，对小样本数据的预测能力较强，已被广泛地应用和研究[13-14]。若隧道变形的初始样本为x(0)，即

x(0)(k)={x(0)(1),x(0)(2),…,x(0)(n)}。

(9)

式中k=1,2,…,n(n为样本个数)。

由于隧道原始监测样本具有波动性和随机性，采用一阶累加进行处理，处理后序列为x(1)，即

x(1)(k)={x(1)(1),x(1)(2),…,x(1)(n)}。

(10)

其中，式(10)对应节点的求解过程为

(11)

而一阶累加序列应满足阶微分方程

dx(1)(t)/dt+ax(1)(t)=b。

(12)

式中：a、b参数与初始序列相关，且满足最小二乘法估计，即

(13)

通过对上述微分方程的求解，其特解即可反推出各节点的预测值，即

x＾(0)(k+1)=x＾(1)(k+1)-x＾(1)(k)(k=1,2,…,n)。

(14)

由于传统灰色模型受输入序列随机性的扰动较大，易导致预测过程中的稳定性及系统误差缺陷。为避免上述问题对预测精度的影响，本文再次将最小二乘法引入到灰色模型的优化过程中。在优化过程中，主要是考虑一阶累加序列的初始值具有一定的不合理性，且随着序列累加阶次的增加，初始值与预测值间的相关性会进一步减弱，进而影响预测模型的精度。因此，本文采用最小二乘法确定初始值，先设定

(15)

式(15)中只要求得c值即可得到初始值的最优估计值，结合最小二乘法原理，式(15)应满足

(16)

通过式(16)对c的求导，即可得到

(17)

通过上述计算，最终确定一阶累加序列的初始值，以达到增加灰色模型稳定性的目的。经优化处理，得到a为2.41，b为4.18。

1.3 BP神经网络

BP神经网络是前馈神经网络，具有多层结构，一般可分为3层(见图2)，分别为输入层、隐含层和输出层，其中各层的节点可根据实例进行设定，且各层间的节点由对应权值进行连接。BP神经网络的传播过程包含了正向传播和反向传播，其中，正向传播指的是输入信息由输入层传至隐含层，再传至输出层，并对比期望结果。若不满足要求，则进入反向传播，对各节点权值进行修正，直到输出结果满足期望要求。

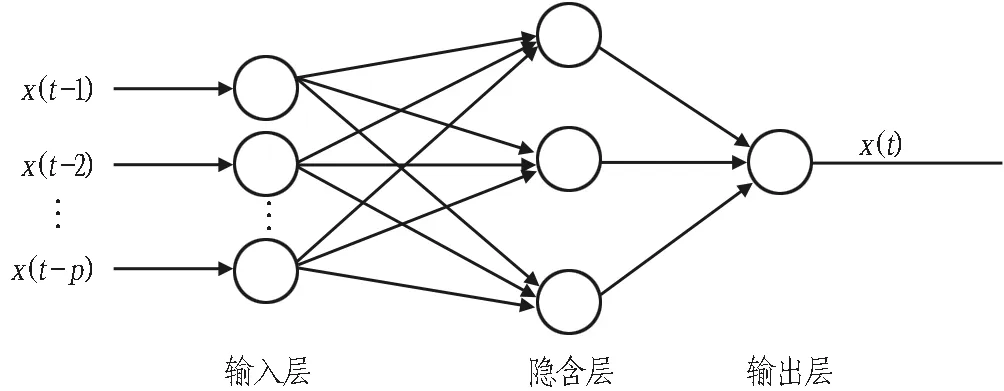
图2 BP神经网络结构图

根据BP神经网络信息传播过程，将其预测过程分述如下。

1)BP神经网络的结构为递推型结构，将输入层节点数设定为6，输出层节点数为1，即以1—6周期预测第7周期； 以2—7周期预测第8周期，以此类推。同时，对模型参数进行设定，如将训练函数设置为train()函数、仿真函数设置为sim()函数、建立函数设置为newff()函数、隐层节点数为10、初始阈值范围为[0,1]等。

2)根据隧道变形的样本信息，将训练样本输入输入层Pk，并正向训练传播至输出层Tk，得到网络训练的输出值Tk*。

3)采用梯度法对各层间的连接权值进行修正，并将输出值与期望值之间的误差表示为

(18)

而权值调整由修正函数确定，即

ωij=ωij+Δωij=ωij+ηδqiγqi。

(19)

式中：δqi为误差修正系数；η为学习因子；i为隐层或输出层节点；q为第q个学习样本。

4)若训练误差达到期望的收敛误差，则停止训练；若训练误差未达到收敛误差，则进入误差反向传播阶段，即重复进入第3步，直到输出结果达到期望要求。

2 实例分析

2.1 实例概况

为验证本文预测模型的有效性，以通省隧道为实例来源[15]，对其变形进行预测。该隧道轴向为235°，属变质岩隧道，围岩为武当群片岩，片理化发育程度较高，是目前国内最长的变质岩隧道，对其变形进行研究具有重要的意义； 同时，围岩的变形具有明显的时间效应特征，大变形时有发生，如右洞YK110+510～+519区间在2012年5月26日出现局部掉块，并引发了施工问题，故对该大变形区间的变形预测具有重要的意义。典型断面YK110+515的监测数据如图3所示。

图3 YK110+515断面变形曲线

由图3可以看出： 1)拱顶及水平变形均具有“S”曲线的特征，在12—22周期的变形均相对较平缓，但在后期变形出现了明显的增加，这与下台阶施工扰动相关； 2)对比拱顶与水平变形的特征，水平变形量均不同程度地大于拱顶沉降量，得出隧道变形以水平收敛为主，分析其原因主要是由隧道下台阶未施工，造成初期支护未封闭引起的。

为进一步分析隧道大变形特征，再对其变形速率进行统计。大变形变形速率特征如表1所示，YK110+515断面变形速率曲线如图4所示。

表1 大变形变形速率特征表

图4 YK110+515断面变形速率曲线

由表1和图4可以看出： 1)拱顶沉降和水平收敛变形速率均具有较大的波动性，且在前期以水平收敛的波动性相对更强，在后期则以拱顶沉降的波动性相对更强，说明在隧道大变形的发展过程中，隧道围岩的应力分布出现了变化； 2)对比拱顶和水平变形的特征参数，得出水平收敛变形较拱顶沉降变形具有相对更小波动性，稳定性相对更好，且拱顶沉降的变异系数为1.03，水平收敛的变异系数为0.8，也进一步说明水平收敛变形的游离性更弱。

2.2 变形预测

采用支持向量机和灰色模型对拱顶沉降进行变形预测，其中，支持向量机也采用递进预测结构，输入节点数仍为6，输出层节点数仍为1； 而灰色模型采用全样本预测，预测结果如表2所示。可以看出： 1)对比各模型的预测精度，具有一定的差异，从侧面可证明本文通过二阶复合结构增加预测模型稳定性的必要性； 2)对比2种模型在优化前后的预测结果，得出通过参数优化，均不同程度地提高了预测精度，说明最小二乘法对2种模型的优化达到了预期目的。

对表2中各模型预测结果的相对误差平均值和方差进行统计，结果如表3所示； 并对预测误差进行对比统计，结果如图5所示。由表3和图5可以看出： 1)对比各模型预测结果相对误差的均值，得出LS-SVM模型的效果最优，均值为1.63%，其次是优化GM(1,1)模型、GM(1,1)模型和SVM模型，且最小二乘法对2种基础模型的预测精度均有一定的提高，但支持向量机模型要优于灰色模型的优化效果，前者提高0.78%的预测精度，而后者提高了0.42%，说明通过最小二乘法能有效地优化预测模型参数，达到提高预测精度的目的； 2)对比各预测模型预测结果的方差，可以得出灰色模型较支持向量机预测结果的稳定性更好，其中，优化GM(1,1)模型的稳定性最佳，方差值为0.151 9，其次是GM(1,1)模型、优化SVM模型和SVM模型； 3)对比各预测模型的预测误差，得出各模型预测结果的差异性较明显，在相同节点具有相反的预测误差值。因此，综合得出优化支持向量机模型具有较高的预测精度，但预测结果的稳定性较弱，而优化灰色模型具有相反的特点，进而本文采用组合方法，将2种优化模型的结果进行组合，组合权值是以误差平方和为指标，分别为0.584 1和0.415 9。

表3拱顶变形预测特征参数统计

Table 3 Statistics of characteristic parameters of crown top deformation prediction

预测方法平均值/%方差SVM2.410.536 5LS-SVM1.630.346 6GM(1,1)2.300.177 5优化GM(1,1)1.880.151 9

通过上述基础预测，再利用BP神经网络对上述预测结果进行修正预测，结果如表4所示。可以看出： 1)通过组合权值的综合，得到组合后预测结果的相对误差均值为0.75%，方差值为0.581 6，得出通过组合预测能较好地提高预测精度，但对预测结果的稳定性提高不大，而通过误差修正的相对误差均值为 0.38%，方差值为 0.167 6，相对前者，预测精度提高了1.97倍，预测结果的稳定性则提高了3.47倍，说明通过误差修正，能较为明显地提高预测精度及稳定性，验证了本文修正模型的有效性； 2)通过对31—34周期的变形预测，得到隧道拱顶后4个周期的变形呈增长趋势，且变形速率相对较大。

图5 拱顶变形预测误差对比

Fig. 5 Comparison between prediction errors of crown top deformation

表4 误差修正预测

2.3 有效性检验

为进一步验证本文预测模型的有效性，本文再以该断面的周边变形收敛数据为基础，采用本文模型进行预测分析，结果如表5所示。可以看出： 1)通过周边变形预测，得到前期预测结果的最大相对误差为1.67%，相对误差平均值为1.34%，方差值为 0.160 2，而误差修正后的最大相对误差为1.32%，相对误差平均值为0.72%，方差值为0.128 0； 2)对比误差修正前后的预测结果，得出修正后提高预测精度和方差分别为1.86倍和1.25倍； 3)对后4个周期的变形预测，得出周边变形仍是呈增长趋势，且增长速率均保持在10 mm/周期之上，34周期的最大变形量已达446.19 mm。

表5周边收敛变形预测统计

Table 5 prediction and statistics of surrounding convergence defor-mation

监测周期周边收敛/mm前期预测结果预测值/mm预测误差/mm相对误差/%BP神经网络预测修正误差/mm预测值/mm相对误差/%25270.99267.393.601.332.14269.530.5426299.22294.294.931.652.03296.320.9727323.19328.49-5.30-1.64-3.19325.30-0.6528349.76352.18-2.42-0.69-3.82348.360.4029377.34371.046.301.671.32372.361.3230402.44398.244.201.042.43400.670.4431413.591.04414.6332425.710.79426.5033438.95-1.42437.5334446.192.84449.03

统计该断面拱顶及周边的变形预测误差，结果如图6所示。可以看出： 1)周边变形预测结果的误差值相对更大，且波动性更强，进而拱顶预测的效果相对更优； 2)分析后4个周期的变形预测结果，综合得出该断面在后期仍具有持续变形的特征，围岩稳定性将进一步减弱，围岩塌方的可能性较大，应采取措施，避免引发的工程施工问题。

图6 拱顶与周边收敛变形预测误差对比

Fig. 6 Comparison of prediction error of convergence deformation between crown top and surrounding

3 结论与讨论

1)通过最小二乘法对支持向量机和灰色模型的优化，构建了两者的优化模型，增强了预测模型参数的准确性，提升了预测模型的预测能力。

2)通过实例验证，得出最小二乘法对支持向量机的优化效果要优于对灰色模型的优化效果，但在预测结果的稳定性方面，优化的灰色模型则具有更高的稳定性，说明不同模型之间的预测结果间具有互补性。

3)在拱顶变形预测的误差修正中，预测精度提高了1.97倍，稳定性提高了3.47倍； 而在周边变形预测的误差修正中，预测精度提高了1.86，方差提高了1.25倍。对比而言，前者的误差修正效果相对更优。

4)综合实例分析的结果，得出本文预测模型具有较高的预测精度及稳定性，且通过了有效性检验，进一步得出本文模型的适用性较广，值得广泛推广和深入研究，但该文预测模型在其他岩土领域中的适用性仍需进一步研究。