基坑土层等效m值反演分析
曹 净, 杨泽帅, 胡 睿, 刘海明
(昆明理工大学建筑工程学院, 云南 昆明 650500)
0 引言
目前,基坑支护结构的设计方法有弹性地基梁法、等值梁法和有限元法等[1]。由于弹性地基梁法考虑了支护结构与土体的变形协调,并且计算模式明确、过程简单[2],在实际工程中得到广泛的应用。但是,目前,工程勘察报告尚不能正确提供各类土层的水平向基床系数[3],而大量工程实践和计算分析均表明,基坑土层水平反力系数的比例系数m值对支护结构的变形和内力影响较大, 甚至影响着基坑支护方案的选择[4]。在具体设计过程中,设计单位通过查阅地勘报告获得m值;若地勘报告中未给出m值,则参考规程和工程经验确定m值。但大多数规程给出的取值范围较大,且每个地区的土体性质存在差异,因此,m值的选取存在很大的随意性[5]。m值的重要性及其难以确定性组成了一个共存且矛盾的问题,是工程设计人员面临的一项难题。
近些年来,国内外许多学者对土层水平反力系数的比例系数m值进行了反演分析研究。文献[6]将光纤测试技术引入基坑监测系统中,得到了施工动态位移反分析技术;文献[7-8]提出基于非参数回归的土层参数反分析算法,利用均匀试验和非参数回归方法构建响应面,并结合可变容差法对土层参数进行反演;文献[9]通过有限元软件进行二次开发得出空间m法,并结合空间m法及位移反分析算法得出围护结构变形性状及开挖的空间效应;文献[10]由单纯形法反演得到的优化位移与实测位移基本接近,验证了反分析法的可靠性。文献[6,9,10]在进行m值反演分析时,直接描述土体力学参数和位移之间的非线性关系,没有考虑土体的物理本构关系,导致缺乏对现象的物理解释。
本文综合上述研究成果,分析提出一个综合考虑土体重度、基坑开挖深度、水平土层反力系数和抗剪强度指标的基坑土层等效m值计算公式,并利用水平位移实测数据和非参数回归方法反演确定系数Δ1、Δ2,以修正所提的等效m值计算公式,最后以昆明某工程实例验证该方法的可行性。
1 基本假设
为获得合理且计算较为方便的基坑土层等效m值公式,作如下假设:
1)假设支护结构底端嵌入坑底土体足够深,当基坑处于弹性抗力状态时,近似地认为支护结构底端的位移量为0,土压力分布大小接近于静止土压力强度;当基坑处于被动极限状态时,支护结构底端产生微小位移。
2)假设嵌固段内土体为同一层土,基坑开挖面附近支护结构的水平位移量为s0。
2 基坑土层等效m 值分析
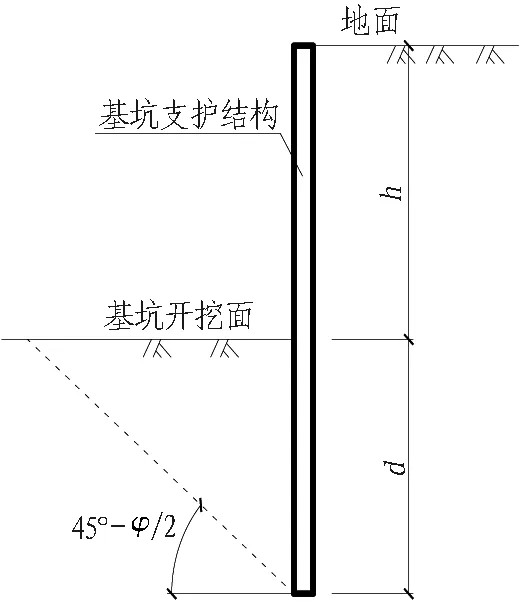
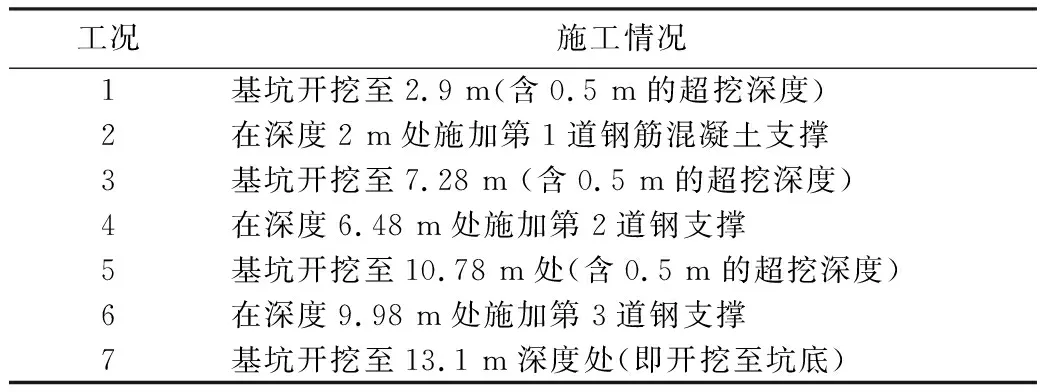
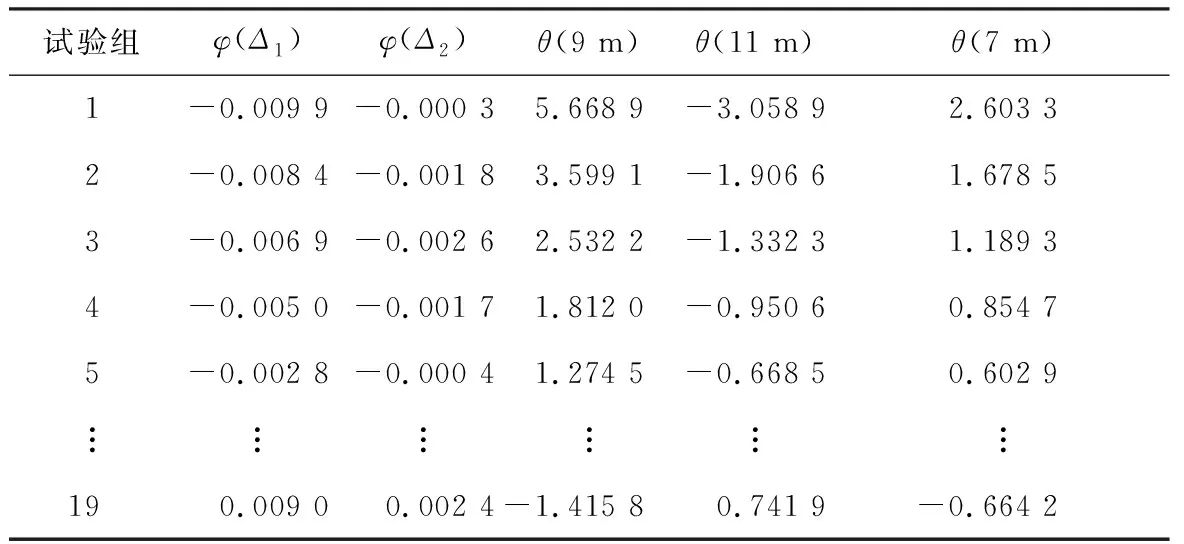
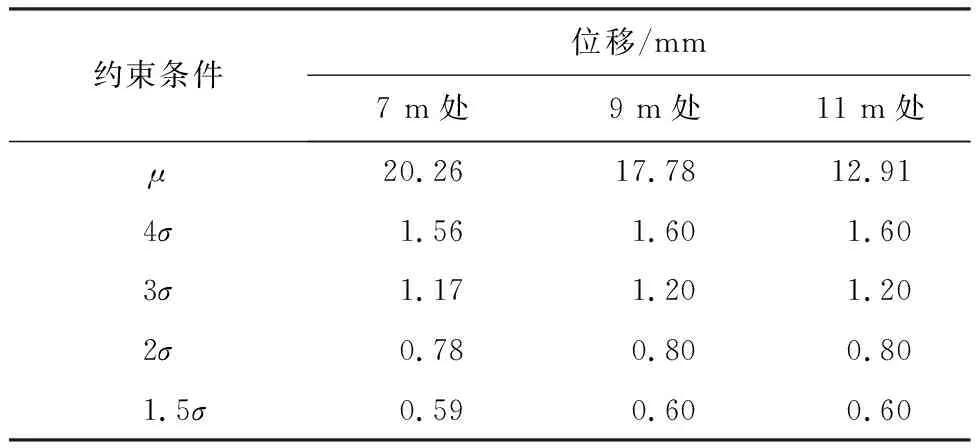
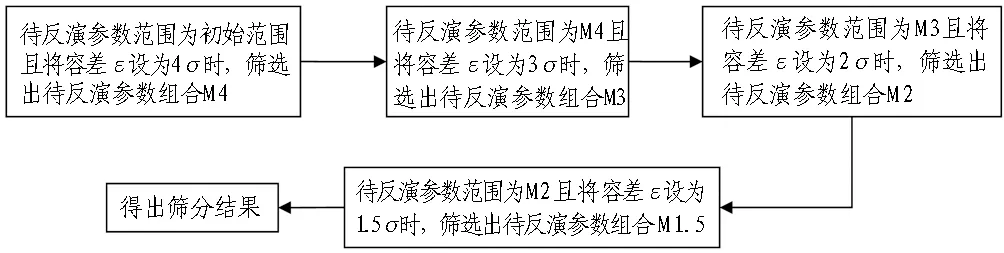
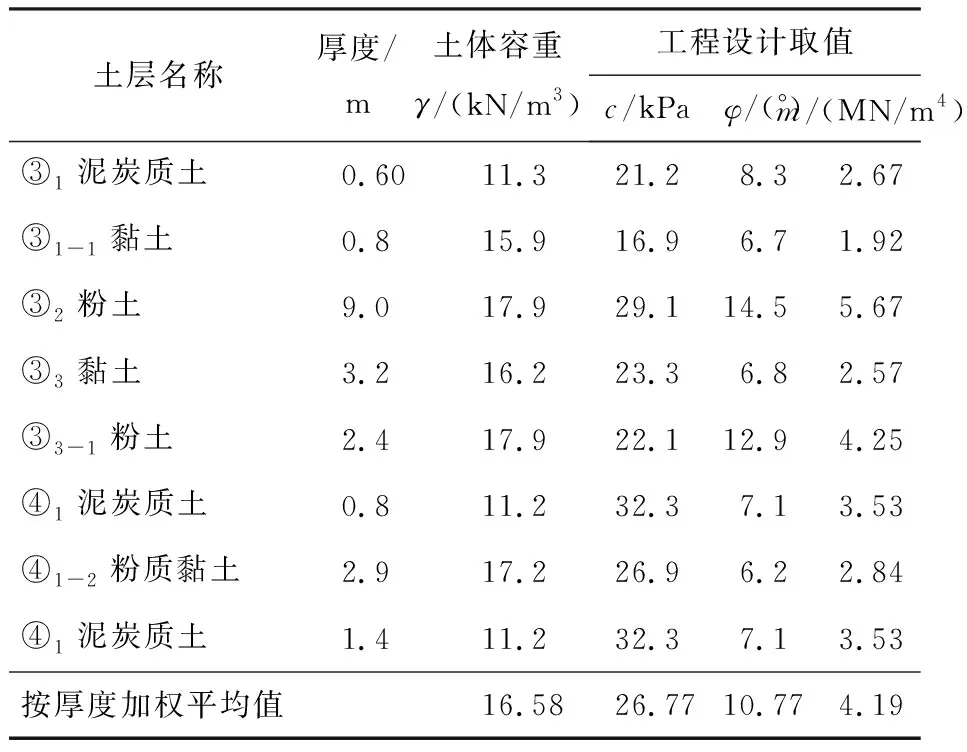
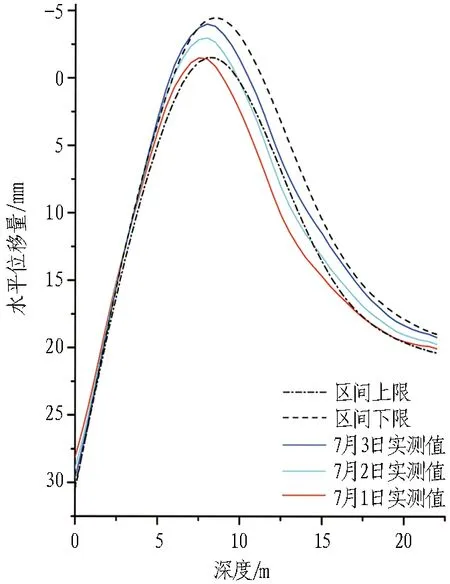
在基坑设计和施工过程中,对支护结构的位移有严格的控制要求,基坑被动区的土体是不允许达到被动极限状态的,其受力状态实际上处于弹性抗力状态。随着基坑的开挖,由于上部土体的卸荷作用,基坑开挖面附近的土体已处于超固结状态,故基坑开挖面的初始土反力系数A0≠0,但由于位移限制的要求,基坑开挖面土体没能达到被动极限状态,即0 A0=2ctan(45°+φ/2)Δ1/s0。 (1) 式中:A0为初始土反力系数,kN/m3;Δ1为水平反力系数的折减系数,0<Δ1<1;s0为开挖面附近支护结构的水平位移量,m;c为被动区土体黏聚力,kPa;φ为内摩擦角。 根据m法,基坑被动区土层水平反力系数 ks=mz+A0=mz+2ctan(45°+φ/2)Δ1/s0。 (2) 式中:m为基坑被动区土层水平反力系数的比例系数,kN/m4;z为基坑开挖面以下某计算点至开挖面的垂直距离,m。 基坑被动区土层水平反力系数的分布如图1所示,其中,基坑开挖深度为h,嵌固段深度为d。 图1 被动区土层水平反力系数分布 Fig. 1 Distribution of horizontal counter-force coefficient in passive zone 当基坑被动区土层处于弹性抗力状态时,σx为由静止土压力和位移引起的挤压应力组成的水平应力(即土反力), σx=k0γz+[mz+2ctan(45°+φ/2)Δ1/s0]δ(z)。 (3) 式中:δ(z)为弹性状态时,计算深度z所对应的支护结构水平位移量,m;γ为土的容重,kN/m3;k0为静止土压力系数,可依据经验公式取k0=1-sinφ′(式中φ′为有效内摩擦角)。 式(3)在基坑嵌固段深度范围内满足: 当z=0时,基坑开挖面的土反力σx=2ctan(45°+φ/2)Δ1;当z=d时,支护结构底端土反力σx=k0γd。 文献[11-12]基于位移土压力的概念,提出被动区土体反力系数为极限被动土压力和静止土压力之差与极限被动土压力引起的支护结构水平位移量之比。若被动区土体达到极限被动状态时, σp=k0σz+ksδp(z)。 (4) 式中:δp(z)为被动极限状态时,计算深度z所对应的支护结构水平位移量,m;σp为被动土压力强度,kPa;σz为计算深度z处的竖向有效自重力,kPa。 水平反力系数 (5) 由朗肯土压力理论得到 (6) 并由此得到被动区水平方向土反力 (7) 将式(7)化简得 (8) 与式(3)进行对比,两式在形式上较为一致,说明由假设得到的式(3)有一定的理论依据。因m法的特点是将被动区土层水平反力系数ks视为随深度呈线性增加的分布模式。式(6)是以基坑嵌固段内土体达到被动极限状态时的位移量相同为前提,若满足条件,说明此时基坑支护结构是经过整体平移达到了被动极限状态,但显然实际工程中很难满足此条件。由式(3)和式(7)对比可知: 基坑土层m值的取值与土体重度、内摩擦角、土层水平反力系数和被动极限状态时的位移相关;被动区土层水平反力系数ks除了与上述几个参数相关,还与土体黏聚力相关。但式(5)的前提是基坑达到被动极限状态,且m法中m值表示的是ks随深度线性增加的斜率。若知道z=d时所对应的δp(z=d),则可进一步确定: (9) 实际基坑因位移控制要求处于弹性抗力状态,故需要在式(9)不等号右侧乘以小于1的水平反力系数的折减系数,得到 (10) 式(10)的m值计算公式量纲是一一对应的,这也说明由假设及分析所得m值计算公式是合理的。 基坑开挖卸荷是一个动态的过程,随着开挖深度的增加,土体抵抗变形的能力将有所降低。通过文献[4,6]对基坑土层m值的反演结果进行分析,表明:m值在基坑开挖过程中并非是固定的,而是随着基坑开挖深度的增加逐渐减小,即基坑被动区土层m值与基坑开挖深度有关。为此,假设支护结构底端z=d时达到被动极限状态,则位移量 δp(z=d)=Δ2h。 (11) 式中:h为基坑开挖深度,m;Δ2是一个远小于1的经验系数。 假设基坑达到被动极限状态模式时(如图2所示),基坑开挖面附近的土体最先受到挤压,先达到被动极限状态。随着转角增大,自上而下各点土体依次进入被动极限状态[13],而此时基坑支护结构底端的水平位移量较小[14],可考虑其趋近于0但不为0。 由文献[15]中被动极限状态时的位移经验公式可大致确定Δ2∈(0,0.01),基坑被动区土层等效m值为 (12) 式中k0为静止土压力系数,k0=1-sinφ′(式中φ′为土体有效内摩擦角,无条件试验时φ′=φ+c[16])。 图2 基坑内侧土体达到被动极限状态模式示意 Fig. 2 Illustration of inner surface of foundation pit in passive limit state 式(12)表明随着基坑开挖深度的增加,基坑土层等效m值相应地降低。实际使用中需将式(12)相关的土层参数按厚度进行加权平均,而公式中系数Δ1、Δ2则需要经过反演分析确定。确定了系数Δ1、Δ2后,可根据基坑开挖深度计算出相应工况的基坑土层等效m值。因此,在建立基坑支护结构的力学计算模型时,被动区土层水平反力系数 (13) 故所建立的基坑支护力学计算模型中包含了与被动区土层水平反力系数ks有关的系数Δ1、Δ2,并将其视为待反演参数,通过直接反演确定其值。 均匀试验是在试验参数范围内通过均匀散布试验样本点的方式,以较少的试验次数获得更多的试验信息,其最大的特点是试验水平相同的条件下,使用均匀试验方法的试验次数比使用正交试验方法的试验次数更少[7]。对于有k个因素X1,X2,…,Xk的试验,采用均匀试验的步骤如下: 1)确定k个因素中每个参数可能的最小、最大值,例如Ximin,Ximax分别为第i个因素的最小值和最大值,i=1,2,…,n,进而确定其范围[Ximin,Ximax]。 2)将每个参数分为k个水平,一般为等分,即 (14) 式中:i为因素序号(i=1,2,…,n);j为水平序号(j=1,2,…,k)。 3)根据因素个数n和所划分的水平数目k选择均匀表Un(kn),再由均匀表确定试验组配。 获得输入数据样本及其对应的输出样本后,需要建立两者之间的响应面关系。本文采用ACE(alternating conditional expectation)拟合技术对其进行回归分析,先不设定响应面函数的形式,而是寻找输入数据x1,x2,…,xn的映射值φ1(x1),φ2(x2),…,φn(xn)和输出数据y的映射值θ(y),使其满足 (15) 式中:i=(1,2,…,n);ε′为反映拟合精度的拟合误差。 从而可以确定响应面函数 y=θ-1[φ1(x1)+φ2(x2)+…+φn(xn)]+ε′。 (16) 式中θ-1[·]为θ[·]的逆函数。 如果确定了φ1(x1),φ2(x2),…,φn(xn)和θ(y),响应面函数关系也就确定了。利用统计数学软件S-Plus中提供的ACE数据包,直接获得各输入数据与输出数据的映射值,从而完成输入数据样本与输出样本之间的响应面关系。 通过式(15)得到所有数据的映射值,再逐一拟合映射值进一步求解θ-1[·],从而建立响应面关系得到式(16)的显式函数形式。若由均匀试验得到的输入因素X1,X2,…,Xk中,每个因素在其计算区间内均有n个计算点,并且是均匀分布的,就可以生成比较密的插值点。对于在计算区间内的任意输入参数xi, 通过响应面关系进行插值运算即可得到其输出的映射值yi。 φi(xi)=interp(Xi,φi(Xi),xi) (i=1,2,3,…,k), (17) (18) 其输出映射值yi=interp(θ(Y),Y,θ(yi))。 (19) 式(17)—(19)中:φi(xi)为与该试验向量相应的变换值; interp(A,B,a)表示a关于向量组(A,B)的插值结果;Xi=[xi1,xi2,…,xin]是由均匀试验确定变量xi的各个水平组成的试验向量;φi(Xi)=[φi(xi1,xi2,…,xin)];Y为试验输出结果向量;θ(y)为其映射值。 在待反演参数可能的取值范围内,通过Monte Carlo模拟枚举出大量样本组合,利用已建立的高效响应面,将计算出的变形值与实测变形值进行对比,筛选出与实测值差异在一定范围内的计算变形值所对应的待反演参数组合。例如,以某工况下的实测水平位移监测数据s为依据,设定一定的容差ε,使位移监测范围为[s-ε,s+ε]作为约束条件(筛子),通过逐步缩小容差ε对比计算变形值和实测变形值,筛选出满足约束条件的计算变形值所对应的待反演参数组合。 昆明市某浅埋公路隧道工程隧道段采用水中围堰明挖法施工,基坑围护结构宽32.9 m,基坑开挖深度最深达14.32 m。 所选剖面基坑深度为13.1 m,采用φ850 mm@600 mm的SMW工法桩,支护桩长29.9 m,型钢为700 mm×300 mm×13 mm×24 mm H型钢。支撑形式为3排对撑,第1排为钢筋混凝土支撑,其水平间距为9 m;第2、3排为钢管支撑,水平间距为3 m,对应施加预应力分别为1 425、1 124 kN。基坑土层力学参数和施工工况分别见表1和表2,基坑支护剖面如图3所示。 表1 基坑土层力学参数表 表2 基坑施工工况 图3 基坑支护剖面 (单位: mm) 因基坑开挖工况的施工用时较短,且测点附近的支护桩变形易受邻近节段土方开挖的影响,支护桩的变形速率并不稳定;而支撑工况的施工是在开挖工况完成后24 h内,且需要间隔一定的时间段才开始下一开挖工况,在此期间,支护桩受外界影响较小,变形速率基本趋于稳定。因此,以基坑支护桩变形数据较稳定的支撑工况(工况4)的监测数据为依据,进行反演分析,工况6则作为验证工况。 本文中待反演参数为Δ1和Δ2,首先对每个待反演参数的区间范围进行假定,详见表3。将上述基坑中每个参数分为20个水平,采用MATLAB自编程序得到均匀表U20(202),进而得到20组参数的输入样本。 表3 待反演参数Δ1、Δ2 的初始范围 本文采用MATLAB软件,基于平面杆系结构的弹性支点法编制基坑支护结构力学计算程序,其中,主动区土体荷载根据《建筑基坑支护技术规程》[17]中相关规定计算,被动区土层反力系数按式(13)计算。由文献[4,8]得出,坑底以下1倍基坑开挖深度范围内的反演结果相对有效,故分别将不同输入样本组代入基坑力学计算模型中,计算出7、9、11 m深度处的水平位移值,并将其作为输出样本,输入和输出数据样本见表4。 表4 输入和输出数据样本 获得了输入和输出数据样本后,利用统计学软件S-Plus中ACE回归的数据包,得出输入样本和9、11、7 m处水平位移值之间的高效响应面。因第1组输入数据Δ1偏小,为了避免对结果产生影响,将其剔除。对剩余19组试验逐一进行回归,其拟合系数均高达0.99,见表5。 表5 映射值 根据已经建立的响应面进行插值运算,利用Monte Carlo模拟技术枚举出10 000个参数样本进行筛选,并计算出10 000个参数样本的支护桩桩身变形值。 在基坑工况4条件下,以支护桩桩顶以下7、9、11 m处的水平位移监测结果作为约束条件,筛选出满足约束条件的计算水平位移值所对应的Δ1和Δ2的组合。其中,约束条件的取值区间为[μ-ε,μ+ε],μ为实测水平位移的均值;ε为容差范围,分别取4σ、3σ、2σ和1.5σ,具体数值见表6。通过不断地缩小容差范围对待反演参数进行筛选,筛分原理见图4。 表6特征点处基坑水平位移的均值与标准差 Table 6 Means and standard deviations of horizontal displacement of foundation pit 约束条件位移/mm7 m处9 m处11 m处μ20.2617.7812.914σ1.561.601.603σ1.171.201.202σ0.780.800.80 1.5σ0.590.600.60 图4 筛分原理 随着容差ε由4σ缩小到1.5σ,得出的筛分结果区间总体趋势在逐渐缩小,反演结果逐渐相对稳定,见表7。因此,将容差1.5σ作为筛分的最终结果。 基坑达到被动极限状态时,被动区深度范围内各点土体所需的位移量并不相等,在开挖面附近的土体受到挤压最先达到屈服强度。随着转角增大,自上而下各点土体依次进入被动极限状态,到支护桩底端时位移量为0.28‰h~0.32‰h(h为基坑开挖深度)。将直接反演得到的Δ1、Δ2取值范围代入式(12),得到该基坑工况4基坑土层等效m值范围为[1.91,2.46] MN/m4(其中土体容重γ、内摩擦角φ和土体水平反力系数k0按厚度取加权平均值)。依据土体抗剪强度指标的标准值,通过《建筑基坑支护技术规程》[17]中4.1.6条的公式计算得到该项目中每层土的m值工程设计值,见表8。而基坑土层等效m值是将基坑被动区等效为同一层土,并且考虑了开挖面附近的初始土反力系数A0,为验证本文的反演结果,将反演得到的Δ1、Δ2参数代入工况6的力学模型中进行分析。 表7 不同容差的反演筛分结果 注: 表中所列数据为参数区间。 表8 基坑土层参数工程设计值 通过工况4反演确定系数Δ1、Δ2后,根据工况6的基坑开挖深度,利用式(12)计算出工况6的等效m值为[1.29,1.66] MN/m4(其中土体容重γ,内摩擦角φ和土体水平反力系数k0同样按厚度取加权平均值),将其代入基坑工况6的力学计算模型中,得到基坑支护桩计算水平位移曲线,并与实测水平位移曲线进行对比,如图5所示。其中,水平位移曲线尾部表示的并非支护桩底部的水平位移,而是测斜管水平位移,支护桩底部比测斜管底长约8 m。通过对比发现,基坑工况6条件下计算变形曲线和实测变形曲线比较接近,证明了本文所述反分析方法的可行性。 工况6的验证结果表明: 基坑被动区土层等效m值直接与支护结构位移相关,经反演分析确定系数Δ1∈[0.252,0.284],系数Δ2∈[0.28‰,0.32‰]。在地质条件相近及周边环境相似的实际工程中,结合地区经验确定取其下限值或上限值,然后根据式(1)和式(12)计算出基坑开挖面处的初始土反力系数A0和基坑土层等效m值并进行分析。对于基坑开挖面处的水平位移s0,为了限制基坑施工中不产生过大变形可取s0=10 mm。 图5 基坑工况6计算变形曲线和实测变形曲线对比图 Fig. 5 Comparison between calculated deformations according to condition 6 and measured ones 本文以现场实测数据为依据,利用均匀试验和ACE非参数回归相结合的方法对系数Δ1和Δ2进行回归分析,以修正所推导的基坑土层等效m值计算公式,并利用该计算公式对基坑工况6进行验证分析,提出了基坑土层m值取值的新方法。 1)本文在假定和简化的基础上,对平面杆系结构弹性支点法中的m值进行了分析,提出了一个综合考虑土体容重γ,基坑开挖深度h,土体水平反力系数k0和抗剪强度指标的等效m值计算公式。随着基坑开挖深度h的增加,m值相应的降低,较为符合基坑的实际受力变形特点,为m值的取值提供了一条新途径。 2)因基坑开挖是一个卸荷过程,本文考虑了因基坑开挖的卸荷作用,开挖面处产生的初始土反力系数A0反演成果更符合实际情况。 3)反演成果缩小了规程及指南给定的m值取值区间,计算精度也相应地提高。所得到的等效m值计算公式考虑了基坑开挖深度的影响,可根据基坑开挖深度不断地修正基坑土层等效m值以实现基坑动态控制。 本文基坑土层m值的计算公式前提是嵌固段为同一土层,当基坑支护结构嵌固段土层竖向分布且性质差异较大时,则需要进一步考虑多层土的等效m值。文中对等效m值公式的推导及反演分析仅限于基坑工程,在其他工程如边坡工程、桩基工程设计中,m值也是一个不可忽视的设计参数,应该对其进行理论及反演分析研究,积累更多经验以便得到一个考虑更为周全的m值计算公式。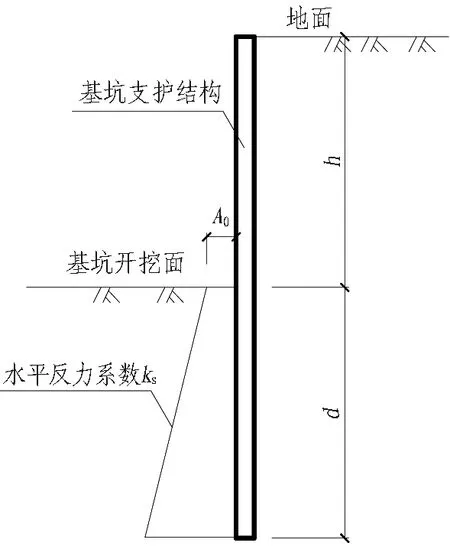
3 反演分析模型的建立
3.1 均匀试验
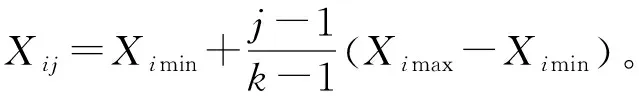
3.2 非参数回归分析
3.3 插值计算

3.4 约束条件
4 算例





5 反演参数的验证
6 结论与讨论

