等比数列在物理解题中的应用例析

浙江 项蔷媛 潘春芳

物理中有一类涉及过程重复发生的问题，即重复发生着几个本质上相同的物理过程。这类问题中不少涉及数列思想方法,考试说明指出，高中物理在考查知识的同时也注重考查学生应用数学解决物理问题的能力,所以涉及数列思想方法的问题自然受到命题者的青睐,在近几年的高考中时有出现,并常作为高考压轴题。为此,有必要对此进行研究,以期引起广大师生的重视，提高解决问题的能力。

从某些个别物理现象或特殊的物理过程出发，可以推论出具有普遍意义的一般性结论，这种从个别到一般，从特殊到普遍的逻辑推理方式叫归纳法。从某个具有普遍意义的一般性原理出发，也可以推论出某一个别的物理现象或特殊的物理过程，这种从一般到个别，从普遍到特殊的推理方式叫演绎法。归纳法和演绎法的交叉应用，是我们解决问题的常见思维方式。过程重复发生的问题,由于重复发生的过程在本质上都是相同的,因而各次过程遵循的物理规律也基本相通,用第一个过程(或对象)的公式和方法一般都可以经过微小的修正后用于第二、第三个过程中。那么,依次列出各个过程所求物理量的表达式,根据归纳法，就可以求得待求物理量的通项公式，从而得以解答问题的目的。

下面主要以典型试题为例介绍求通项公式的方法:归纳法和演绎法，不妥之处，敬请雅正。

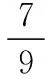
【解析】每碰撞一次后小球做竖直上抛运动，可分为上升和回落两个阶段，这两段所用时间和位移大小相等。

小球原来离地面高度为4.9 m，用h0表示，下落到地面时的速度v0应为：

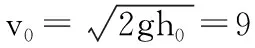
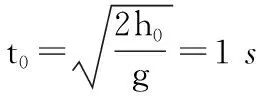
接下来用演绎法：

小球第一次和地面碰撞后的速率：

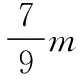
第一次与地面碰撞后上升、回落需用时间：

小球第二次和地面碰撞后的速率：

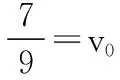
第二次与地面碰撞后上升、回落需用时间：

再用归纳法：

所以小球从开始到下落n次碰撞后静止所用总时间为：

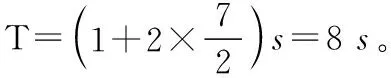
【点评】此题中小球与地面碰撞无数次，试图求出每一次的时间将是无止境的，很是考验学生的心智。关键利用演绎法和归纳法找出小球第n次碰撞后在空中运动的时间tn的表达式，看看tn的表达式有何规律(此题中tn符合等比数列规律)，然后利用有关数学等比数列知识求得最后结果。

【拓展变式】试求小球从开始下落到停止运动所经过的路程。

【参考答案】19.91 m

【例2】一个质量为m、带有电荷-q的小物体(可视为质点)，可在水平轨道Ox上运动，O端有一与轨道垂直的固定墙、轨道处于匀强电场中，其场强大小为E，方向沿Ox轴正方向，如图1所示。小物体以初速度v0从x0点沿Ox轨道运动，运动时受到大小不变的摩擦力f作用，且f﹤qE；设小物体与墙碰撞时不损失机械能，且电荷量保持不变，求它在停止运动前所通过的总路程s。

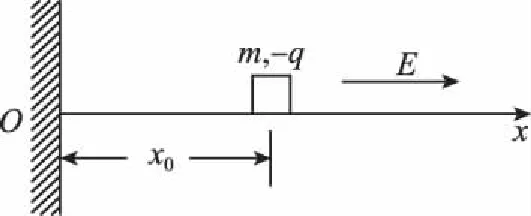
图1

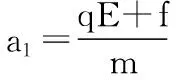
解法一：等比数列法

首先用演绎法：

再用归纳法：

依此类推，小物体第n次与墙碰后的速率：

所以小物体在停止运动前所通过的总路程：

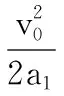
解法二：动能定理法

注意到本题由于摩擦力总是做负功，物体机械能不断损失，所以物体通过同一位置时的速度将不断减小，直到最后停止运动。物体停止时，所受合外力必定为零，因此物体只能停在O点。

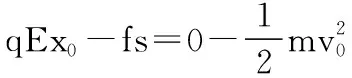
解法三：能量守恒法

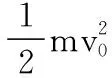
【点评】本试题解题策略开放，问题本身存在不止一种解法，它能通过灵活应用物理知识、运用不同物理思维方法解答物理问题，考查学生思维的灵活性。

【例3】某仪器用电场和磁场来控制电子在材料表面上方的运动，如图2所示，材料表面上方矩形区域PP′N′N充满竖直向下的匀强电场，宽为d；矩形区域NN′M′M充满垂直纸面向里的匀强磁场，磁感应强度为B，长为3s，宽为s；NN′为磁场与电场之间的薄隔离层。一个电荷量为e、质量为m、初速为零的电子，从P点开始被电场加速经隔离层垂直进入磁场，电子每次穿越隔离层，时间极短，运动方向不变，其动能损失是每次穿越前动能的10%，最后电子仅能从磁场边界M′N′飞出。不计电子所受重力。

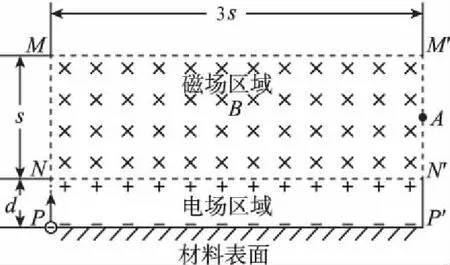
图2

(1)求电子第二次与第一次圆周运动半径之比；

(2)求电场强度的取值范围；

(3)A是M′N′的中点，若要使电子在A、M′间垂直于A、M′飞出，求电子在磁场区域中运动的时间。

【解析】(1)设圆周运动的半径分别为R1、R2、…、Rn、Rn+1…，第一和第二次圆周运动速率分别为v1和v2，动能分别为Ek1和Ek2，则：

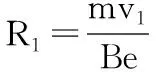
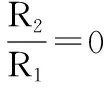
(2)设电场强度为E，第一次到达隔离层前的速率为v′,则：

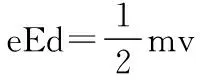
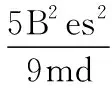
又由(限于篇幅，演绎法和归纳法具体不再展开)：

Rn=0.9n-1R1

2R1(1+0.9+0.92+…+0.9n+…)=3s

(3)设电子在匀强磁场中，圆周运动的周期为T，运动的半圆周个数为n，运动总时间为t，由题意，有：

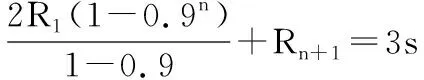
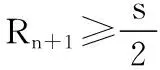
得：n=2

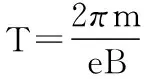
【拓展变式1】改变设问的角度：

(1)控制电子在材料表面上方运动，最大的电场强度是多少；

(2)若电子以上述最大电场加速，经多长时间将第三次穿越隔离层？

【拓展变式2】可改变控制电子运动的区域方位及磁场的方向(具体步骤略)。

【改编题】为了控制和调节材料表面逸出的电子在材料表面附近的运动，小明在材料表面右侧分别设置了长为l、宽为d的矩形均匀电场和均匀磁场区域，如图3所示。电场方向水平向左，大小为E；磁场方向垂直纸面向外，在磁场与电场之间有一薄隔离层。一个电荷量为e、质量为m、初速为零的电子，从P点开始被电场加速经隔离层垂直进入磁场，电子每次穿越隔离层，时间极短，运动方向不变，其动能损失是每次穿越前动能的20%，通过调节磁感应强度，控制电子最后仅能从垂直磁场上边界QN(Q为MN的中点)区间飞出。已知l=3.816d，不计电子所受重力。求：

图3

(1)电子从P点第一次到达电场右边界时的速度v0；

(2)磁感应强度B；

(3)电子在电场区间运动的时间tE。

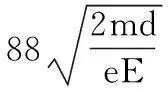
【点评】对此例可以看出：

(1)模型典型：本题涉及的物理问题代表了一类问题，带电粒子在复合场中(分列电场和磁场)的运动。该类模型涉及两个典型问题：粒子在电场中的运动和在磁场中的运动，通过该题的学习，就能加深理解和掌握这一类问题，提高复习效率；

(2)知识厚重：本题涉及的物理知识相对较多，有力学、电磁学、能量等，所以知识相对厚重；

(3)过程丰富：先在匀强电场中做匀加速直线运动，紧接着穿越隔离层有能量损失，进入磁场中做匀速圆周运动，经过一段时间后到达隔离层再穿越隔离层能量又损失，进入电场中做匀减速运动，直到速度减为零，之后反向重复前一过程，体现运动的周期性特征，非常考验学生的分析能力；

(4)难度梯度适当：入口浅，设问逐步深入，学生比较容易上手，但还是很考验学生应用数学知识解决物理问题的能力；

(5)方法基本：本题主要运用匀变速运动规律，匀速圆周运动规律，以及利用数学知识解决物理问题的能力。