拨开云雾见日出——一道橡皮筋问题的进阶学习

安徽 王 云 牛 丽 周有顺

遵从胡克定律的弹簧、弹性绳、橡皮筋是力学中常见的模型，无论是平衡问题还是非平衡问题均涉及。此类模型的解题过程往往能够体现化静态为动态、化单向为多向的思维方式，考查了综合应用数学方法解决物理问题的科学探究能力，且解题方法较为灵活，隐形条件较难发现。下面以一道涉及橡皮筋的动态平衡问题为切入点进行分层学习的探讨，希望能给读者带来启示。

【例题1】如图1所示,一根遵从胡克定律的橡皮筋,其一端系于O点,另一端系一物块,橡皮筋的原长为OA,竖直时物块对地面有压力,在水平拉力作用下物块缓慢地向右沿直线运动，则在运动过程中

( )

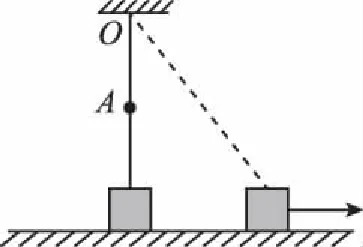
图1

A．地面对物块的支持力保持不变

B．地面对物块的支持力减小

C．地面对物块的摩擦力增大

D．地面对物块的摩擦力减小

【解析】物块在水平拉力作用下缓慢地向右沿直线运动时处于动态平衡状态，合外力等于零。如图2所示，以O点为圆心，以橡皮筋原长OA为半径作圆弧与OD相交于C点，CD为橡皮筋的伸长量，另做CE垂直BD并交于E点;如图3，对物块进行受力分析。

图2

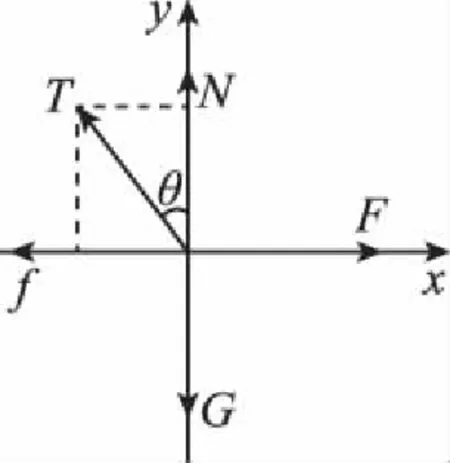
图3

构建共点力平衡方程得

F-f-kxCDsinθ=0,N+kxCDcosθ-G=0

物块与地面间的弹力为

N=G-kxCDcosθ=G-kxCE

物块与水平地面间的滑动摩擦力为

f=μN=μ(G-kxCDcosθ)=μ(G-kxCE)

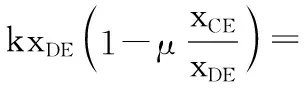
选项BD正确。

【反思】动态平衡问题的核心思想是“以不变应万变”，分析过程中务必明确哪些物理量不变，哪些物理量变化且动态源怎样变化，合理采用数学工具进行定量分析更加有利于科学思维的建立。本题的难点是橡皮筋绕O点转动，通过几何方法确定伸长量为CD，并通过共点力平衡条件进行定量推导，同时随着物块向右运动，物块与地面间弹力逐渐减小，物块可能离开地面。所以本题为了严谨性，需要补充条件“物块缓慢地向右直线运动一小段距离”。

【变式1】如图4所示，若在靠近A点右侧的位置固定一枚光滑钉子，则在水平拉力作用下，物块缓慢地向右沿直线运动，则在运动的过程中

( )

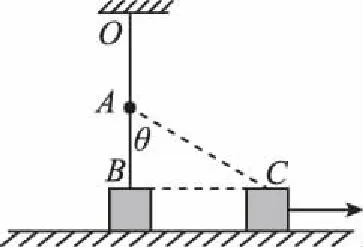
图4

A．地面对物块的支持力保持不变

B．地面对物块的支持力减小

C．地面对物块的摩擦力增大

D．水平拉力保持不变

【解析】此情形受力情况与图3类似，利用共点力平衡可以推导。

物块与地面间的弹力N=G-kxACcosθ=G-kxAB

物块与水平地面间的滑动摩擦力f=μN=μ(G-kxAB)

水平外力F=μ(G-kxAB)+kxACsinθ=μ(G-kxAB)+kxBC

选项A正确。

【反思】此变式最大特点为条件“靠近A点右侧固定一枚光滑钉子”，则AC段为橡皮筋的伸长量，所以弹力在竖直方向的分力保持不变，物块与地面间弹力则不变，滑动摩擦力保持不变，橡皮筋伸长量在水平方向的分量逐渐增大，则水平方向的分力逐渐增大，水平外力逐渐增大。

【变式2】如图5所示，若在A点上方有一点M，靠近M点右侧固定一枚光滑钉子，在水平拉力作用下物块缓慢地向右沿直线运动，则运动的过程中

( )

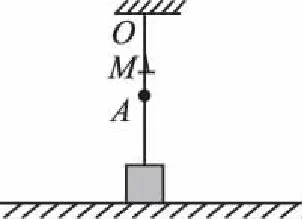
图5

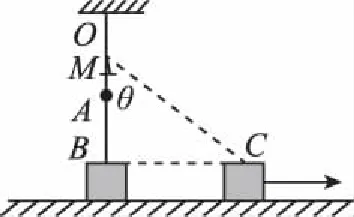
图6

A．地面对物块的支持力保持不变

B．地面对物块的支持力减小

C．地面对物块的摩擦力增大

D．水平拉力保持不变

【解析】此情形如图6所示，其受力情况与图3类似，利用共点力平衡可以推导。

物块与地面间的弹力为

N=G-k(xMC-xMA)cosθ=G-kxMB+kxMAcosθ

物块与水平地面间的滑动摩擦力为

f=μN=μ(G-kxMB+kxMAcosθ)

水平外力F=μG+k(xMC-xMA)sinθ(1-μcotθ)

选项B正确。

【反思】此变式最大的特点是“在A点上方靠近M点右侧固定一枚光滑钉子”，xMC并非为橡皮筋的伸长量，所以在计算过程需要利用(xMC-xMA)代表伸长量。

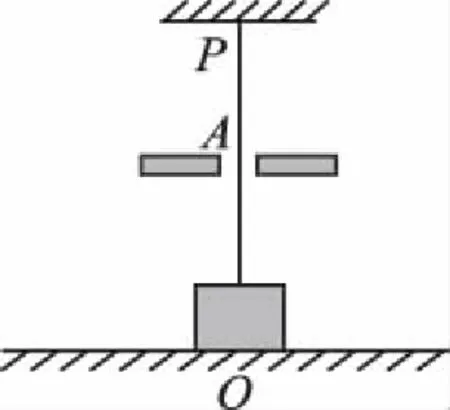
图7

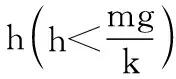
【解析】假设物块在C点摩擦力恰好为最大静摩擦力，根据共点力平衡可以求解。则滑块处在以O点为圆心，以r为半径的圆内如图9所示，都可以保持静止。

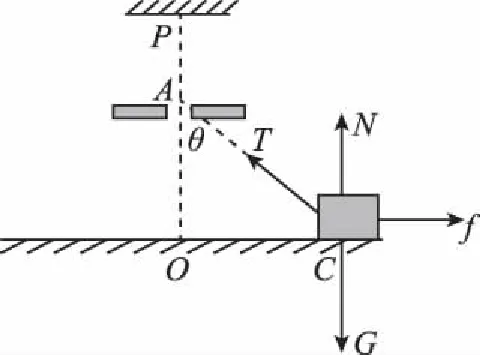
图8

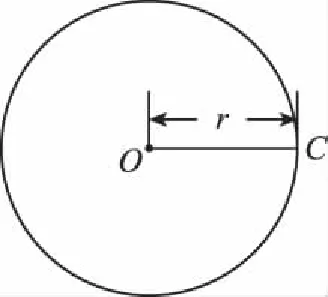
图9

受力分析如图8所示，由平衡方程有

fm-kxACsinθ=0

N+kxACcosθ-G=0

fm=μN

且r=xACsinθ,h=xACcosθ

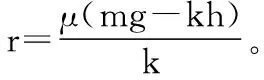
【反思】物理情境从二维平面进化到三维立体，运动区域从直线进化到二维平面，利用降维思想便于学生思维的建立，解题关键是AC段为伸长量。

【例题2】如图10所示，用橡皮筋将一小球悬挂在小车的架子上，系统处于平衡状态。现使小车从静止开始向左加速，加速度从零开始逐渐增大到某一值，然后保持此值，小球稳定后偏离竖直方向某一角度(橡皮筋在弹性限度内)。与稳定在竖直位置时相比，小球高度

( )

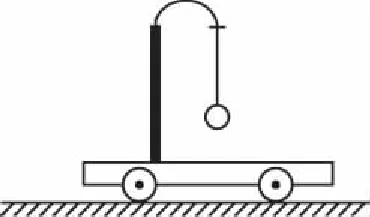
图10

A.一定升高

B.一定降低

C.保持不变

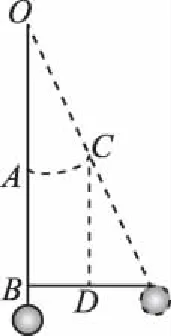
图11

D.升高或降低由橡皮筋的劲度系数决定

【解析】如图11所示，以悬点O点为圆心，以橡皮筋原长OA为半径作弧，与倾斜后的橡皮筋相交于C点，小球在竖直方向保持平衡，所以橡皮筋的伸长量在竖直方向的投影和AB相等，显然小球稳定后小球的高度会升高。选项 A正确。

【反思】与例题1的平衡问题分析具有异曲同工之妙，从平衡进化到非平衡是思维一次质的飞跃，两者之间有区别也有共同点，学习的精髓在于通过发散、比较、归纳等方法寻找具有普遍性的规律。

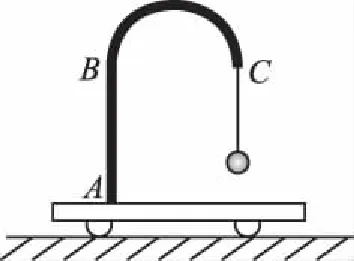
图12

【变式】如图12所示，AB为一固定在小车上的竖直杆，BC为一光滑弯曲管道，橡皮筋一端固定在支架上的B点，穿过管道的另一端悬挂一个小球，系统平衡时，BC弧长恰好为橡皮筋的原长，现使小车向左做匀加速运动，小球稳定地偏离竖直方向某一角度(橡皮筋在弹性限度内)。与稳定在竖直位置时相比，小球的高度

( )

A．一定升高

B．一定降低

C．保持不变

D．升高或降低由橡皮筋的劲度系数决定

【解析】此变式的特点“BC为一光滑弯曲管道，且BC弧长恰好为橡皮筋的原长”，所以C点以下部分恰好为橡皮筋的伸长量，小车向左做匀加速运动，但小球竖直方向保持平衡，橡皮筋的伸长量在竖直方向的投影保持不变，所以小球的高度保持不变。

选项C正确。

【反思】例题2及其变式也可以设置小球做圆锥摆运动，运动轨迹从直线变化为曲线，研究小球的高度随角速度的增加会发生怎样的变化。