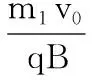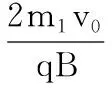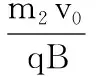粒子收集问题分类透析

浙江 刘 伟

利用探测器收集到粒子是获取粒子之间、粒子与物质之间相互作用信息的先决条件，在微观研究领域有着广泛的应用。基于粒子收集为背景的高考题不胜枚举，浙江省实施新高考以来，五次选考中连续考查三次就已突显了重要性。

就考查动向而言，该类问题侧重于解决收集板收集时，粒子出现的位置、范围、比例、时间和作用力等问题。如图1为从粒子源发射粒子到探测器收集粒子过程中的一些要素关系的分析。

图1 匀强磁场中粒子收集问题的要素关系

我们知道，点状粒子源各向均匀地向外发射粒子时，粒子沿收集板的分布是不均匀的，反之亦然，有时粒子源也会存在沿确定方向直线发射粒子的情形。考虑到收集的实际情况，一般会控制粒子速度矢量(大小、方向)、磁感应强度大小和粒子比荷等变量、初始方位、收集板长度和磁场范围等空间约束条件，由此粒子的收集情形呈现多维化和复杂性的特征，从而使得该类问题能有效地区分不同思维层次和问题解决能力的学生的水平。

考虑到发射状态、收集情形的形式多样，约束因素众多，本文以发射状态和收集情形为基本线索，依据空间和物理变量的约束条件，参照常见题境进行梳理辨析。

一、粒子由粒子源均匀发射确定收集的时间、区域和比例等问题

1.源板对称——无约束变量，即收集板关于粒子源与收集板的垂线对称放置

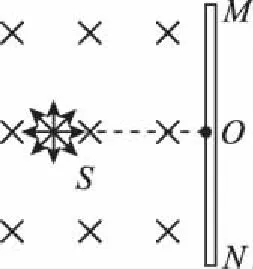
图2

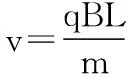
【问题1】确定粒子到达收集板的时间极值及时间差。

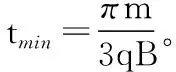
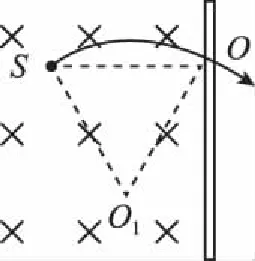
图3

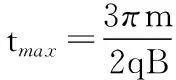
图4

【评注】磁场确定时，粒子轨迹所对的圆心角越大，运动时间就越长。对于弦长则存在两种情况：轨迹为劣弧时，弦长越长，圆心角越大，优弧则相反。因此，我们可以把粒子源到收集板的垂线作为击中的最短弦长，对应着最短时间；比较粒子轨迹与收集板两端的相切情况，由圆心角来确定最长时间。

【问题2】确定粒子出现在收集板上的区域范围。

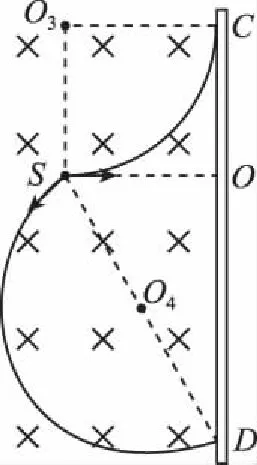
图5

【评注】出现在足够长收集板的区域范围一般是一端轨迹与收集板的相切点，另一端是以粒子源为圆心，以粒子在磁场中运动的直径为半径所作的圆与收集板的交点，这两个点位就是粒子出现在收集板上的极值位置。如果只改变粒子电性或磁场方向，则粒子将做顺时针转动，此时击中两端点的情形互换，但总长度仍不变。

【问题3】确定收集板上粒子重复出现的区域范围。

【分析】以S→O为正方向，粒子速度方向按逆时针与正方向间的夹角设为θ。如图6所示。

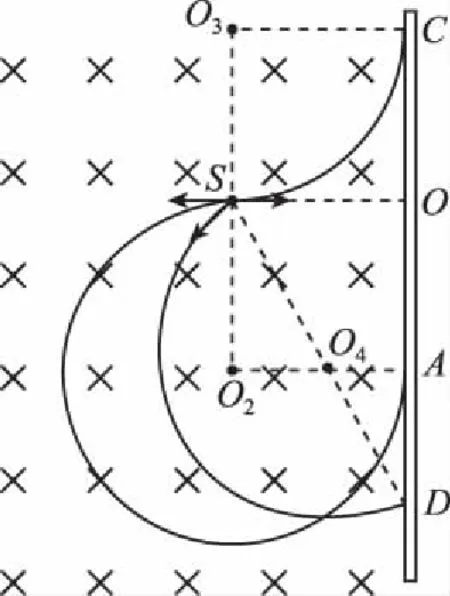
图6

(1)当θ=180°时，以O2为圆心的圆弧，首先击中收集板下端的A点。

(2)当θ逐渐减小时，轨迹与收集板的交点逐渐单调下移。

(3)当θ=150°时，以O4为圆心的圆弧，击中收集板的最下端D点。

(4)当θ继续减小时，轨迹与收集板的交点将一直单调上移。

(5)当θ=0°时，以O3为圆心的圆弧，击中收集板的最上端C点。

【评注】随着速度方向的渐次变化，粒子往往先从一端相切击中收集板为起始，再从另一端相切离开收集板。就击中位置而言，其取向不是单调而是有往复的，重复区域为其中一相切点与击中最远点的间距。

【问题4】确定粒子收集比例及其与源板间距满足的关系。

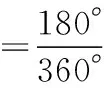
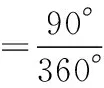
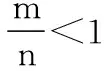
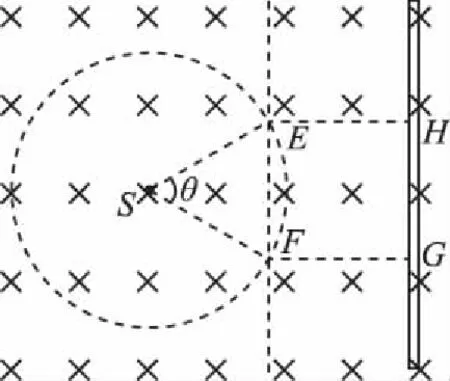
图7

【评注】粒子轨迹与收集板的两端相切点，分别对应着粒子源发射粒子击中板的临界状态，其角度范围内的全部粒子均能击中收集板，是击中板的粒子数范围，区别于击中板的长度区域范围，通过角度范围可以确定击中的粒子数比例，以及给定比例下的收集板位置等。

2.源板对称——空间约束

空间的约束主要来源于有界的磁场或有限的板长，导致不是所有的粒子都会偏转或偏转后的粒子将掠过收集板的两端，因而要比较无约束情况下的粒子轨迹确定收集情形。

若磁场有界，如图8所示，粒子处于有界磁场的竖直左边界上，例1中的其他条件均不变，则到达收集板的最短时间不变，最长时间所对应的圆心角为90°，此时到达收集板区域的最高点仍相切，最低点对应着沿磁场边界向下发射的粒子轨迹；而沿磁场边界向下的速度方向若顺时针转动，粒子将射出磁场，因此收集板上将不再出现粒子重叠区域。

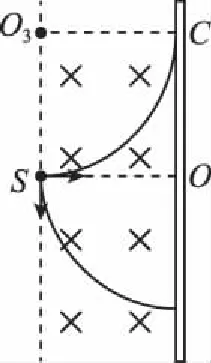
图8

若板长有限，如图9所示，收集板长为2L，例1中的其他条件均不变，则粒子到达收集板的时间差不变，此时到达收集板区域的最高点仍相切，最低点对应着下端相切的粒子轨迹；由于粒子可能的重叠区域都在板长之外，因此也不会出现粒子重叠的情况。

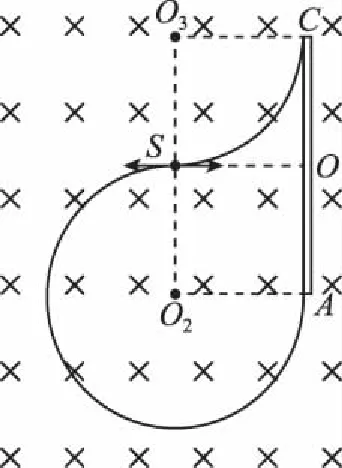
图9

二、粒子在收集板上均匀分布确定收集的数量、比例、板受力情况等问题

粒子源发射粒子是非均匀的，而在收集板上粒子分布是均匀的。这种情形粒子偏转轨迹比较清晰，往往通过粒子比荷、磁感应强度大小和速度大小等变量的设置来改变轨迹的半径，通过速度方向来控制收集板上粒子出现的范围。就粒子源与收集板的空间方位来看，一般是两者共线的情况。

1.源板共线——变量约束求收集范围、比例，即粒子源与收集板在同一直线上

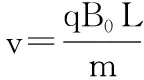
图10

【问题5】速度方向改变，确定收集范围。

【分析】如图11所示，关于y轴对称的左边界和右边界粒子击中收集板的同一位置，θ越大击中点离发射点O越近。

选取速度的右边界，由几何关系知

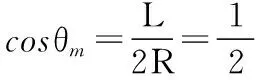
此时所有粒子均被收集，θm=60°是最大的速度偏移方向。

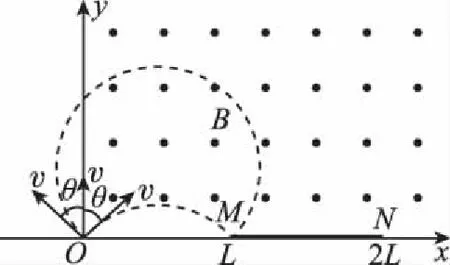
图11

【评注】速度方向的约束制约了收集范围。对称的速度方向将击中收集板的同一点，速度方向的偏移范围决定了出现在收集板上的距离的极值问题，且θ值与粒子出现的最近点位置一一对应。

【问题6】磁感应强度大小改变，确定收集比例。

若粒子到达x轴时沿x轴均匀分布。当θ=37°，在磁感应强度B取不同值时，求单位时间内收集到的粒子数比例η与磁感应强度B之间的关系。

【分析】根据磁感应强度B的大小，可以把收集比例分成三种情况即全部收集、部分收集和不收集，对应着五个收集区域。由题意知B=B0时，粒子出现的最远点恰好在N处。

(1)若最近点在M处,2R1cosθ=L,B01=1.6B0,B0≤B≤1.6B0,粒子全部收集,即η=100%。

(2)若最远点在M处，2R2=L，B02=2B0，则B>2B0，粒子全部不收集，即η=0。

(3)若最近点在N处，2R3cosθ=2L，B03=0.8B0，B<0.8B0粒子全部不收集，即η=0。

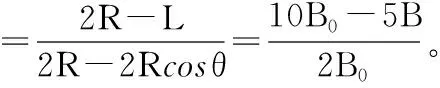
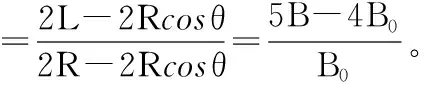
【评注】由于粒子运动半径随着磁感应强度大小而变化，从而确定了收集比例的问题。粒子收集存在着四个临界：运动到达的最近、最远点和被收集的最左、最右两端点。可以先通过临界比较确定收集比例的极值情况，再从收集板的左端到右端，有序给出部分粒子收集的比例关系。

2.源板共线——变量约束求受力

【问题7】速度大小变化，确定板的受力情况。

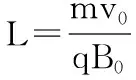
【分析】先确定单位时间在收集板上的粒子数目N：

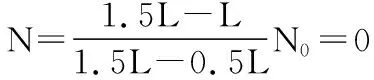
根据动量定理，有

吸收的粒子受到收集板的作用力大小为

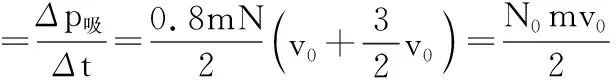
反弹的粒子受到收集板的作用力大小为

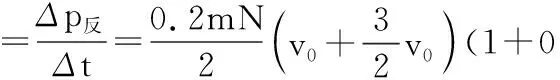
根据牛顿第三定律，收集板受到的作用力大小为

【评注】如果粒子在收集板上均匀分布且沿板方向速度与粒子源间距线性变化，则在应用动量定理时，其初末动量分别等于收集板两端点动量的算术平均值。

【问题8】比荷变化，确定叠加区域。

在例2中，正粒子源沿y轴正方向发射不同比荷的两种粒子甲和乙，甲、乙的质量分别为m1、m2(m10)，速率均在v0≤v≤2v0范围内变化。其他条件不变，求甲、乙粒子在x轴上的叠加区域。