直觉模糊推理的三I约束算法

井 美，惠小静，王 蓉

延安大学 数学与计算机科学学院，陕西 延安 716000

1 引言

1965年，Zadeh提出了模糊集[1]。针对模糊集理论，诸多学者进行大量地研究，并已将模糊集理论广泛运用到模式识别、医疗诊断、模糊控制等领域[2-3]。模糊推理是模糊集理论研究的重要方面，它的核心问题是以下形式的FMP、FMT：

（1）规则 A→B （2）规则 A→B

输入 A∗输入 B∗

输出 B∗输出 A∗

这里的A,A∗是论域X上的模糊集，B,B∗是Y论域上的模糊集。1973年，Zadeh提出了著名的CRI算法[4]，但是由于它缺乏严格的逻辑基础且不具有还原性，于是，王国俊教授提出了全蕴涵三I算法[5]，有效地弥补了CRI算法的不足，并将其纳入模糊逻辑系统之中。

直觉模糊集[6]是由Atanassov提出的，它是模糊集的推广，而且能更好地反映日常事物的模糊性和不确定性。有关直觉模糊集的理论已经广泛应用到聚类分析、模式识别、群决策等领域[7-9]，但是直觉模糊集在模糊推理方面却没有得以迅速的发展。主要由于直觉模糊蕴涵算子比模糊蕴涵算子复杂得多，从而使它的理论体系并不完善。首先文献[10-11]对直觉模糊蕴涵算子的相关理论进行了初步的研究，文献[12]对直觉模糊推理作了深入研究，文献[13]提出了剩余型直觉蕴涵算子，从而为直觉模糊集与模糊推理之间建立了内在联系，在此基础上，文献[14-15]研究了剩余型直觉模糊推理的三I算法。

目前，将直觉模糊集与其他推理方法相结合的研究甚少，为此，本文将直觉模糊集与文献[16]提出的三I约束算法结合起来，研究了直觉模糊推理三I约束算法，当然对于模糊集上的FMP、FMT问题也同样推广到直觉模糊集上，称之为IFMP、IFMT问题，进一步讨论了IFMP、IFMT问题的直觉模糊推理三I约束算法解的表达形式和分解形式。直觉模糊集是模糊集的推广，所以说直觉模糊推理三I约束算法也是模糊推理三I约束算法的推广，本文也给予了论证。

2 预备知识

定义2.1[6]设X是论域，x∈X，X上的直觉模糊集 A是指函数μA(x)、νA(x)、π(x)满足下列条件的三元组：

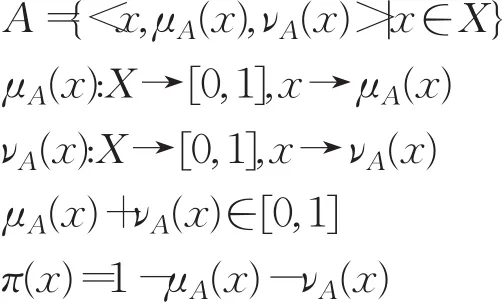
其中对于任意的x∈X，称μA(x)为隶属度函数，νA(x)为非隶属度函数，π(x)为犹豫度度函数，也称不确定度函数。

特别的，∀x∈X ，μA(x)+νA(x)=1，则称直觉模糊集A退化为模糊集。

定义2.2[14]设X、Y为非空论域，X、Y上的直觉模糊集分别为 IFS(X)、IFS(Y)。

令 IFS={(t,f)|t,f∈[0,1],0≤t+f≤1}，定义 IFS上的一个偏序关系-≺如下：

（1）α,β∈IFS，α=(a1,a2)，β=(b1,b2)，α≤β当且仅当a1≤b1，a2≥b2。

（2）α∨β=(a1∨b1,a2∧b2)，α∧β=(a1∧b1,a2∨b2)，最小元 0∗=(0,1)，最大元 1∗=(1,0)。显然可知，(IFS,-≺)是完备的分配格。

定义2.3[14]若(⊗,→)构成伴随对，(⊕,⊖)构成余伴随对，且(⊗,⊕)对偶，则称→,⊕,⊖为⊗的关联算子。

引理2.1[14]L=[0,1]，若→,⊕,⊖为⊗的关联算子，则∀a,b∈L，b⊖a=1-(1-a)→(1-b)。

注 在本文中出现的运算优先如下：

⊗,⊕,⊖→,∧,∨,高于+,-

定义2.4[17]⊗是L上的三角模，若二元运算⊕满足：a⊕b=1-(1-a)⊗(1-b)，则⊕是L上的三角余模，称⊕为与⊗对偶的三角余模。反之，⊕是L上的三角余模，若二元运算⊗满足：

a⊗b=1-(1-a)⊕(1-b)

则⊗是L上的三角模，称⊗为与⊕对偶的三角模。

定义2.5[14]⊗是L上的三角模，⊕是L上与⊗对偶的三角余模，在IFS上定义二元运算⊗∗,⊕∗：α⊗∗β=(a1⊗b1,a2⊕b2)；α⊕∗β=(a1⊕b1,a2⊗b2)。

定理2.1[14]设⊗∗是由左连续三角模⊗生成的直觉三角模，则IFS上存在二元运算→∗使得α⊗∗β≤γ当且仅当α≤β→∗γ，并且

β→∗γ=∨{η∈IFS|η⊗∗β≤γ}

命题2.1[14]设⊗∗是IFS上左连续的直觉三角模，且(⊗∗,→∗)是 IFS 上的直觉伴随对，则

（1）γ →∗(α →∗β)=α →∗(γ →∗β)。

（2）α≤β→∗γ当且仅当 β≤α→∗γ。

（3）1∗→∗α=α 。

（4）α→∗β关于第一变元α单调递减，关于第二变元β单调递增。

定理2.2[14]α,β∈IFS，α=(a1,a2)，β=(b1,b2)，→∗

是由IFS上左连续的直觉三角模⊗∗生成的剩余型蕴涵算子，则下列结论成立：

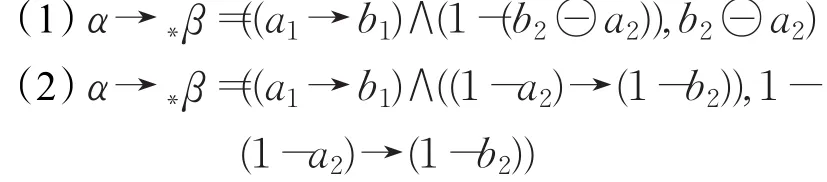
3 IFMP问题的直觉模糊推理三I约束算法

IFMP问题的直觉模糊推理三I约束原则：

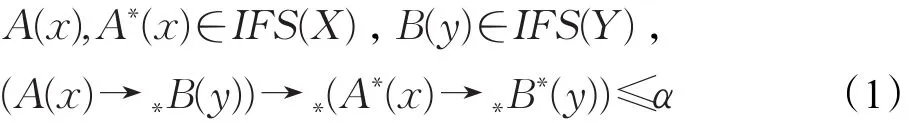
则B∗(y)是IFS(Y)中满足式（1）的最大直觉模糊集。

定理3.1设(⊗∗,→∗)是 IFS上的直觉伴随对，则IFMP问题的直觉模糊推理三I约束算法的解B∗(y)可表示为如下：

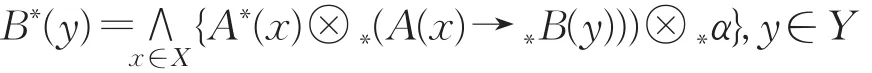
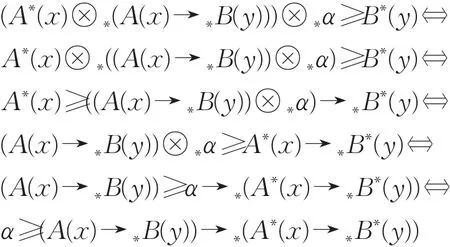
从而可知 B∗(y)满足式（1）。现在证明 B∗(y)为满足式（1）的最大直觉模糊集。

假设存在 C(y)∈IFS(Y)，使得 C(y)满足式，即(A(x)→∗B(y))→∗(A∗(x)→∗C(y))≤α

由IFS上的伴随对(⊗∗,→∗)的性质可知：

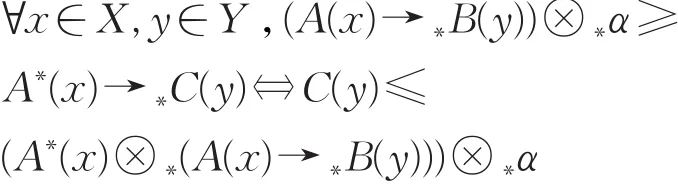
因此 C(y)≤B∗(y)。所以 B∗(y)为IFMP问题的直觉模糊推理三I约束算法的解。

推论3.1设(⊗∗,→∗)是 IFS上的直觉伴随对，B∗(y)=((y),(y))，α=(a1,a2)，则IFMP问题的直觉模糊推理三I约束算法的B∗(y)可分解如下：

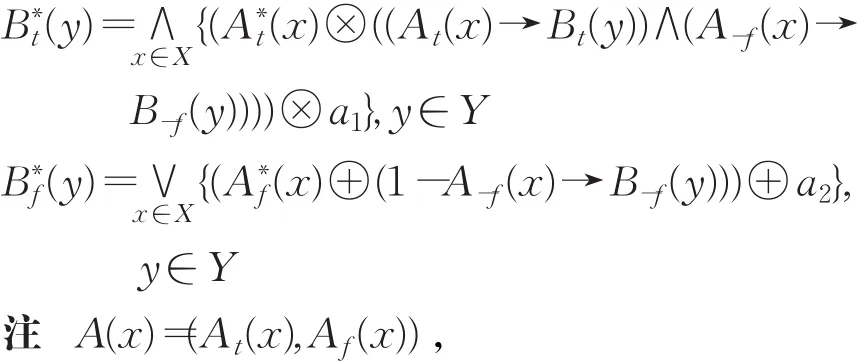
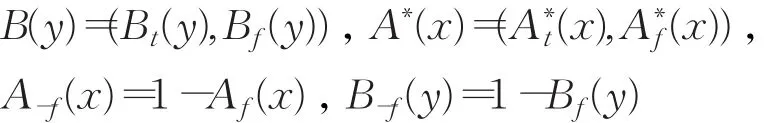
模糊集是直觉模糊集的特例，直觉模糊集是模糊集的推广，所以直觉模糊集推理三I约束算法也是模糊推理三I约束算法的推广。若IFMP问题的直觉模糊集A,A∗,B退化为模糊集，那么对于定理3.1中给出的B∗是否也是模糊集，它和FMP问题的模糊推理三I约束算法解是否一致，给出下面的定理。

定理3.2[18]设→为正则蕴涵算子，⊗是与→伴随的三角模，a为常数，则FMP问题的模糊推理三I约束算法解可表示为如下：

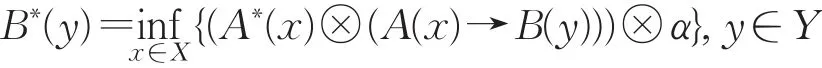
定理3.3若A,A∗,B退化为模糊集，则定理3.1中B∗是也是模糊集，而且它和定理3.2给出的FMP问题的模糊推理三I约束算法解是一致的。

采用BP神经网络算法对电动汽车充电负荷进行日预测。先用四组日负荷值对BP神经网络进行学习训练，在达到要求后，用4组日负荷值进行日负荷预测。结果记为y1。具体步骤如此：

证明 若A,A∗,B退化为模糊集，则满足以下条件：

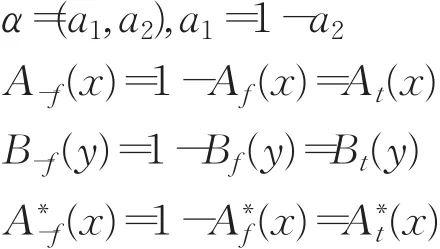
由定义2.5和定理2.2可知：

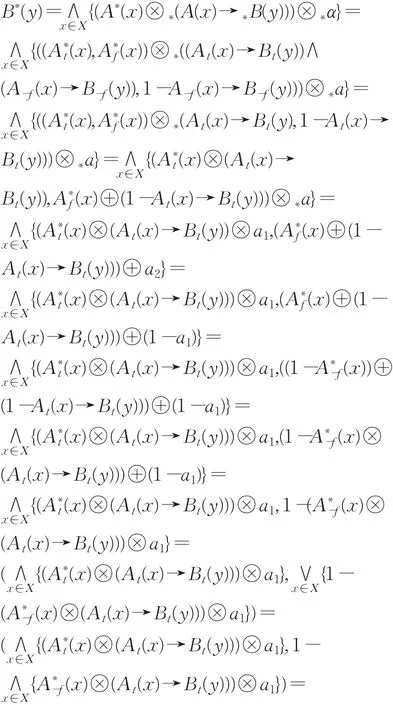
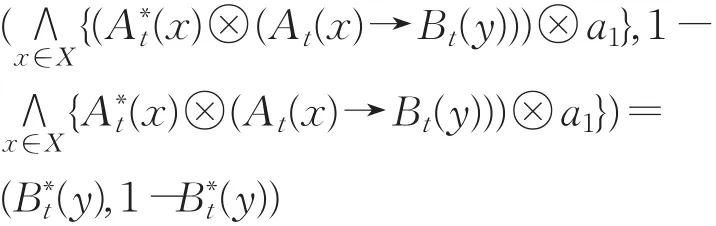
4 IFMT问题的直觉模糊推理三I约束算法

IFMT问题的直觉模糊推理三I约束原则：A(x)∈IFS(X)，B(y),B∗(y)∈IFS(Y)，α∈IFS，则A∗(x)是IFS(X)中满足式（1）的最小直觉模糊集。

定理4.1设(⊗∗,→∗)是 IFS上的直觉伴随对，则IFMT问题的直觉模糊推理三I约束算法的解A∗(x)可表示为如下：

证明 由A∗(x)的表达式，命题2.1及引理3.1可知：

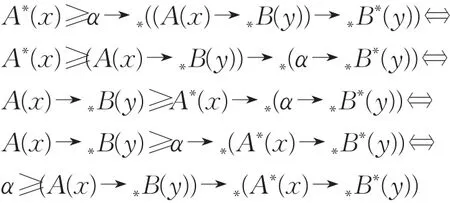
从而可知 A∗(x)满足式（1），现在证明 A∗(x)为满足式（1）的最小直觉模糊集。

假设存在 D(x)∈IFS(X)，使得 D(x)满足式（1），即(A(x)→∗B(y))→∗(D(x)→∗B∗(y))≤α 。

由IFS上的伴随对(⊗∗,→∗)的性质可知：

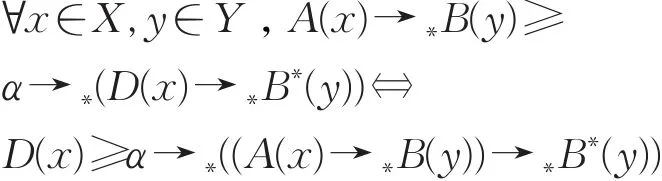
因此 A∗(x)≤D(x)。所以 A∗(x)为IFMT问题的直觉模糊推理三I约束算法的解。

推论4.1设(⊗∗,→∗)是 IFS上的直觉伴随对，A∗(x)=(A∗t(x),A∗f(x))，α=(a1,a2)，则IFMT问题的直觉模糊推理三I约束算法的解A∗(x)可分解如下：

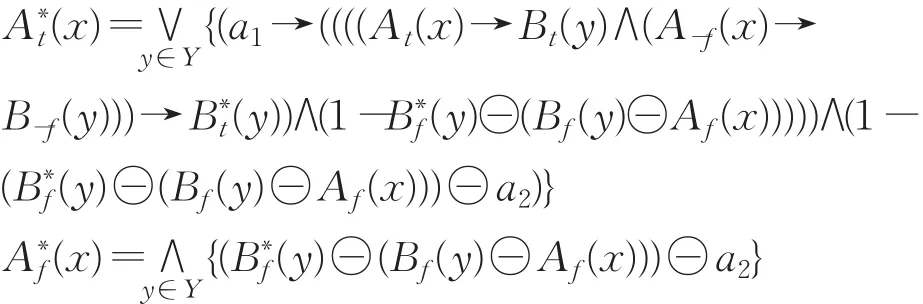
注 A(x)=(At(x),Af(x))

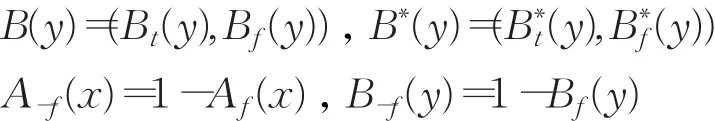
模糊集是直觉模糊集的特例，直觉模糊集是模糊集的推广，所以直觉模糊推理三I约束算法也是模糊推理三I约束算法的推广。若IFMT问题的直觉模糊集A,B,B∗退化为模糊集，那么对于定理4.1中给出的A∗是否也是模糊集，它和FMT问题的模糊推理三I约束算法解是否一致，给出下面定理。

定理4.2[18]设→为正则蕴涵算子，⊗是与→伴随的三角模，a为常数，则FMT问题的模糊推理三I约束算法解可表示为如下：

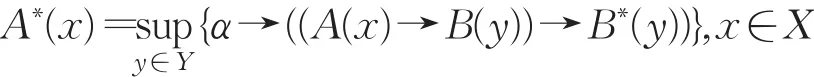
定理4.3若A,B,B∗退化为模糊集，则定理4.1中的A∗也是模糊集，而且它和定理4.2给出FMT问题的模糊推理三I约束算法解是一致的。

证明 若A,B,B∗退化为模糊集，则满足以下条件：

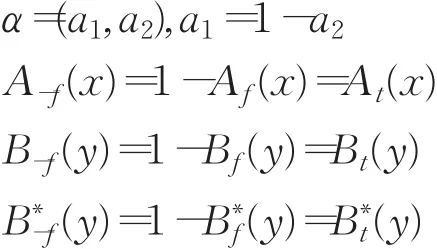
由引理2.1和定理2.2可知：

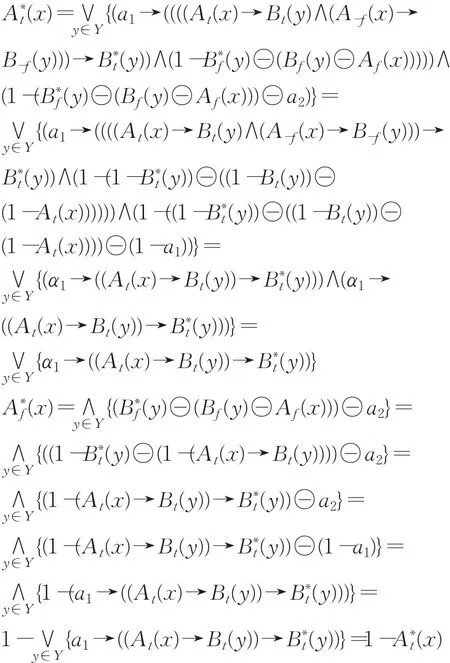
5 结束语

直觉模糊集作为模糊集的推广，已经广泛应用到聚类分析、模式识别、群决策等领域。本文研究的直觉模糊推理三I约束算法，为直觉模糊集在模糊推理方面的研究提供了新的思路。一方面丰富和发展了对直觉模糊集的研究，另一方面本文的思想和方法均可用以研究其他算法，比如直觉模糊推理的反向三I算法，直觉模糊推理的泛三I算法等。