测量参数未知随机系统的多模型对偶控制算法∗

孙晋坤 杨恒占

（西安工业大学电子信息工程学院 西安 710021）

1 引言

实际工业生产过程中总是存在各种不确定性。除了噪声的不确定性外，往往还存在测量设备参数的不确定性。在这种背景下，从20世纪70年代起，随着计算机技术的快速发展，基于对偶控制思想的多模型对偶控制（Multi-Model Dual Control，MMDC）得到了深入的研究和发展［1～4］。多模型对偶控制根据系统的实际变化情况和控制要求，将系统在不同情况下的系统结构和参数采用不同的辨识模型描述，针对各个子辨识模型分别设计对应的子控制器［5］，符合解决复杂问题的基本规律，因而受到国际控制界的广泛重视和深入研究［6］。

现有的多模型统计特征控制大都属于模型的组合切换方式，或多或少都存在着切换过程不够平滑的问题。本文在系统参数的后验概率加权方法的基础上，将各个模型使用协调变量进行融合归一，利用归一后的模型对系统进行控制，改善了控制过程的平滑性。

2 问题描述

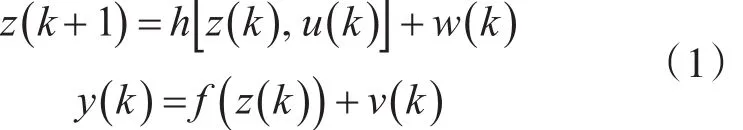
其中，z(k)为n维状态向量，u(k)为q维控制向量，y(k)为 p维量测向量，w(k)为n维过程噪声，v(k)为 p维量测噪声；h为n维非线性函数，f为p维非线性函数。该系统中，f的参数均为全部未知或部分未知，或者虽然已知但是过于复杂，无法

考虑如下离散时间随机系统：用传统方法进行有效量测。

衡量控制器控制效果的性能指标采用如下的加权二次型性能函数：

为表述简单，本文仅讨论A、B、C为定常矩阵的情况。

式（2）中，k为控制时间，假定从0到N-1。对于随机系统（1），在k时刻，可以收集到的信息集ϕk为

实际上，ϕk也是k时刻能够知道的所有信息。因此，控制器u(k)约束为：u(k)=μk(ϕk)。

本文的目的就是确定一个形式为上式的控制函数u(k)，使式（2）所表述的性能指标J在统计意义下取得最小值，即：

本文采用一组子模型覆盖被控系统的不同工作状况。假设共有s个工作状况，分别对应s个子模型，则该组模型的数学描述如下：

MG={ }Mi|i=1，2，…，s

MG为s个子模型组成的集合。假设第i个子模型为

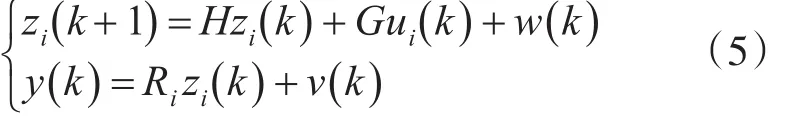
上式中，zi(k)为第i个子模型Mi的状态向量，ui(k)为第i个子模型的控制向量；Ri为具有适当维数的矩阵，表示不同工作状况下量测系数。zi(k)的初始状态为zi(0)，zi(0)和过程噪声w(k)、量测噪声v(k)互不相关且都为高斯白噪声，它们服从的分布特征分别为：zi(0)～N(zˉ0， F0)、w(k)～N(0 ，W ) 、v(k)～N(0 ，V ) 。

针对式（2）所示的性能指标 J，在第i个子模型已知的情况下，由于模型参数都是已知的，该问题就是标准的LQG控制问题，相应的成熟解法已经存在。但是，本文讨论的问题存在着系统当前量测参数未知即当前子模型未知的困难。针对该困难，本文将各模型的后验概率作为协调变量，凝聚出单一的融合模型，再使用LQG成熟方法得到合适的控制律u(k)，使控制器既能辨识出合适的模型，又能保持良好的控制性能。

3 控制器设计

3.1 模型固定情况下的控制器设计

在k时刻，可以收集到的信息集为ϕk。假若时刻k系统的真实模型为第i个子模型，则状态zi(k )基于 ϕk的估计值 ẑi(k |k)为

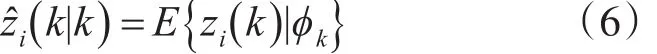
由Kalman滤波方程，ẑi(k|k)的递推式子为

其中

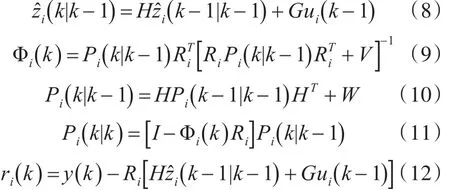
上式中，边界条件为 ẑi(0 |0)=ẑ(0)及Fi(0 |0)=F0。

k时刻系统的真实模型为第i个子模型Mi，根据动态规划原理，由标准的LQG控制算法，最优控制ui(·)的递推式子为

其中

3.2 多模型情况下的控制器设计

首先计算各子模型的后验概率。假设第i个子模型Mi在k时刻的后验概率为 ρki，即

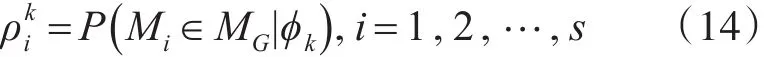
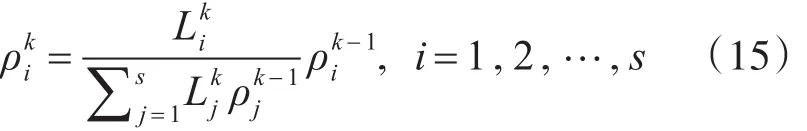
其中

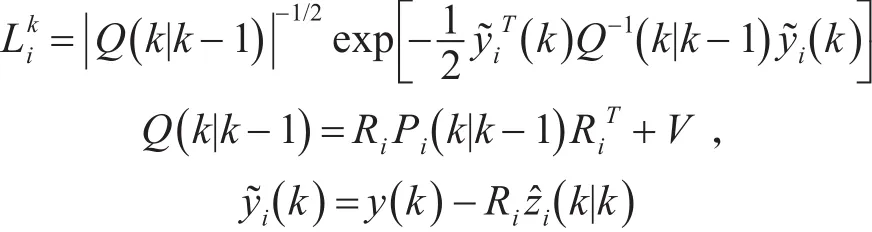
在初始k=0时刻，对每个模型的偏好是一样的。在k时刻，各个子模型对应的各自的滤波器并行工作，因此能够得到各自的后验概率。

令

考虑如下最优控制问题：

对于该最优控制问题来说，其系统模型就是通过后验概率将模型集MG中各个子模型凝聚而成的融合模型。

针对该单一融合模型，本文利用Bellman动态规划思想求解控制律u(k)。令

转换上式形式，有

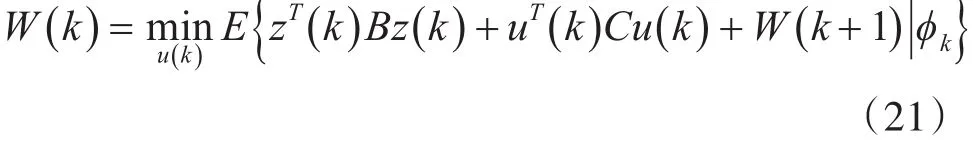
且

划方程。式（21）对应的最优控制律u(k)为

其中

相关递推式子的初始值为S(N)=A。控制增益K(k)采用动态规划的方法获得。

4 仿真分析

考虑如式（5）所示随机系统，两个子模型分别为

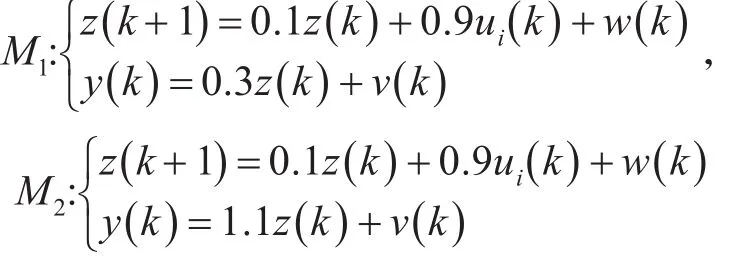
控制总步数N为100。在时间1～50内，系统的真实模型为M1；在时间51系统的真实模型发生突变，由子模型M1切换到子模型M2，且一直保持到到 时 间 100。 其 中 μ（x），η（x）=0.242exp(x-0.5x2)，初始状态x(0)～N(0.5 ， 0.25) 。性能指标函数为

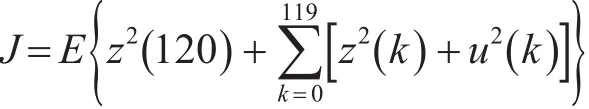
与最优控制进行比较，如图1所示。可以看出虽然多模型控制的性能指标比最优控制要差一些，主要是模型辨识阶段性能指标较差，但在对真实模型的辨识基本完成后，两者的性能指标变化趋势基本一致。

图1 多模型低阶统计特征对偶控制与最优控制

5 结语

本文分析了参数未知多模型系统的参数辨识和控制问题，应用分解-协调思想，提出了一种多模型对偶控制方法。该方法体现了对偶控制参数学习与目标跟踪的双重作用，也改善了子模型硬切换导致的系统震荡问题。用后验概率把多个子模型融合为单一模型，具有明显的优点。