螺栓连接松动的导波监测技术综述
,
(西北工业大学航天学院,西安 710072)
0 引言
螺栓连接作为主要的可拆连接方式已被广泛应用于航空航天结构中[1]。在使用过程中,螺栓连接存在着多种可能的失效模式,包括螺栓松动、连接界面滑动和分离、疲劳裂纹和断裂等[2]。由于安装过程中的预紧力加载不当,以及服役期间承受的各种时变载荷或其他环境因素作用,螺栓松动成为其中最常见的问题。关键部位的螺栓松动会直接导致整个结构的失效,因此对螺栓预紧力进行监测对于确保结构的安全性和可靠性至关重要。
在航空航天领域,随着飞行器结构复杂化与服役环境的恶劣化,结构健康监测技术(Struc-tural Health Monitoring,SHM)成为保障结构安全性与可靠性的重要手段,是航空航天力学与环境工程领域的前沿技术之一。根据国际航空航天工业SHM指导委员会的定义[3],结构健康监测是指通过在被监测结构中集成传感器,并从传感器获取和分析数据以确定结构健康状况的过程。结构健康监测技术具有结构功能一体化集成、原位监测和实时在线诊断的能力,目前已有较多利用SHM方法开展不同结构系统中螺栓松动监测问题的研究[1]。常用的技术方法主要有基于振动、基于机电阻抗和基于导波的SHM技术3类。在基于振动的SHM 技术中,结构整体的动态特性,如固有频率、模态和频率响应函数等被用于检测螺栓松动[4]。然而,由于组装结构通常由很多螺栓组成并且螺栓连接是局部结构元件,所以局部位置处的螺栓松动不会导致整体结构动态特性的显著改变[5]。因此,基于振动的SHM技术对于螺栓预紧力的变化并不敏感,导致该技术的监测灵敏度较差。基于机电阻抗的SHM技术通过监测螺栓连接部机械阻抗的变化来确定螺栓预紧力[6-7]。在该方法中,通常需在紧靠螺栓连接的部位黏贴压电传感器(PZT),由于PZT的电阻抗与机械阻抗耦合,从而可以通过测量电阻抗的变化识别出螺栓预紧力的变化[8-9]。已有研究表明,使用机电阻抗技术可以实现螺栓松动的有效监测[10-12],但它的检测范围局限于压电传感器附近[13],并且需要昂贵的高精度阻抗分析仪[14],因此存在一定的局限性。
基于导波的SHM技术在过去20年得到了深入的发展[15-16]。近年来,由于导波较大的检测范围和较高的灵敏度,基于导波的螺栓预紧力监测方法吸引了越来越多学者的关注[1],被认为具有极大的工程应用潜力[17]。本文针对螺栓连接预紧力的导波监测方法及相关理论、技术进行综述,目的是梳理该技术的发展现状和重要突破,为推动该领域的技术发展和工程应用提供一定参考。
1 理论背景与数值建模
1.1 理论背景
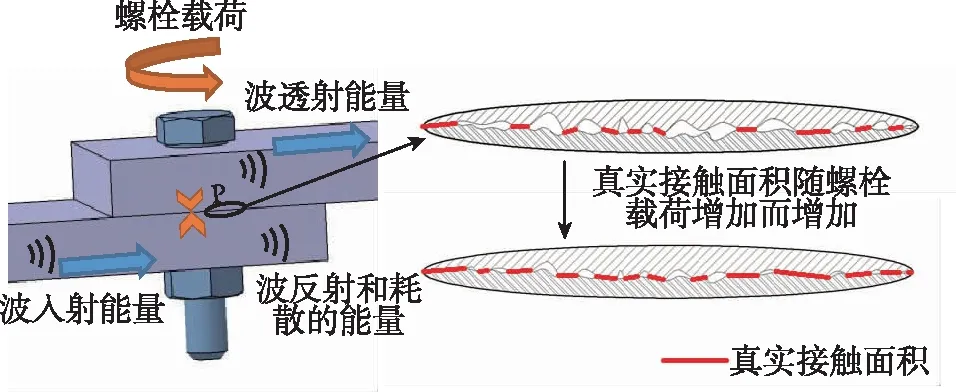
图1 超声导波在螺栓连接部的传播示意图Fig.1 Schematic of guided wave propagationthrough bolt joint
典型的螺栓连接结构一般由螺栓、螺母和两个被连接部件组成。从微尺度的角度来看,连接界面上覆盖了大量的微凸体,实际接触面积是每对接触微凸体接触面积的总和。随着螺栓预紧力增加,界面处的接触压力增加,相应地更多微凸体发生接触,微凸体间的接触面积同时增加,因此总的实际接触面积随之增加。当超声波通过搭接面时,只有一部分入射波能量可以透射过搭接部,另一部分被反射回去或耗散(见图1)。为定量化的解释上述过程,美国斯坦福大学Yang等[4]利用Hertz接触理论和正弦波表面形貌模型来描述粗糙表面接触,以此得到了真实接触面积与接触压力之间的关系。其理论分析结果表明,通过连接结合面的导波能量与结合面真实接触面积成正比,同时真实接触面积随着螺栓预紧力的增加而增加。尽管上述理论分析中没有考虑粗糙接触面上存在塑性变形,同时接触面形貌并不能用正弦曲线完全描述,但Yang等[4]的理论分析与实验结果较为一致。此后,超声导波的透射波能量作为拧紧指数被广泛用作螺栓松动监测,然而根据粗糙接触力学理论,当接触压力达到一定值时,连接界面处的真实接触面积会达到饱和值[18],此时真实接触面积不再随着接触压力的增加而变化。因此利用透射波能量检测时,当螺栓预紧力达到一定值后,透过的导波能量不再变化,此时其检测灵敏度会显著降低。
由于螺栓连接部中包含接触界面,因此导波传入螺栓连接部后信号中会有非线性特征,这些非线性特征也可以被提取并用于螺栓预紧力检测。与之相对应,前面所提到的导波能量变化未考虑非线性的影响,可以称之为线性特征。在基于非线性特征的方法中,接触声学非线性(Contact Acoustic Nonlinearity, CAN)正引起越来越多的关注。螺栓松动后在受到一定幅度的声波或振动的激励时,连接界面会承受一定的拉压力,导致界面周期性的开合,进而导致界面刚度的周期性变化,因此结构响应呈现非线性,称为接触声学非线性[19-20]。为激励连接界面的非线性特征,需要很大的导波幅值,由于压电元件的激励幅值一般较小,很难激起结构本身的非线性,为此目前学者常用振动声调制(Vibro-acoustic Modulation, VM)、冲击调制(Impact Modulation, IM)这两种方式实现基于CAN的螺栓预紧力监测[21]。这两种方法的主要区别在于,IM采用冲击力来激发被测结构的振动,而VM通过谐波施加稳定的振动来激发被测结构的振动。VM方法和IM方法的本质在于接触界面与振动和波混合激励的相互作用。当螺栓连接结构中的所有螺栓完全拧紧时,获得的信号谱分别在振动和波频率处显示两个峰值。当螺栓松动时,频谱中的波频率附近会出现额外的频率分量,称为左边频带和右边频带。边频带的幅值由CAN的强度决定,因此也可以与螺栓预紧力建立关联关系[22]。
为了定量描述导波信号频谱中的边频带幅值与螺栓预紧力之间的关系,Zhang等[22]建立了螺栓连接部CAN的单自由度理论模型,如图2(a)所示。基于该模型的分析结果表明,边频带的幅值与非线性接触刚度K2呈线性比例关系,该非线性接触刚度取决于接合界面处的接触压力。 随后,Zhang等[23]提出了模拟螺栓连接结构的两自由度非线性模型,以此分析次谐波的物理现象及其产生条件,如图2(b)所示。在此基础上,其对于使用次谐波的螺栓连接预紧力检测的有效性进行了理论验证。
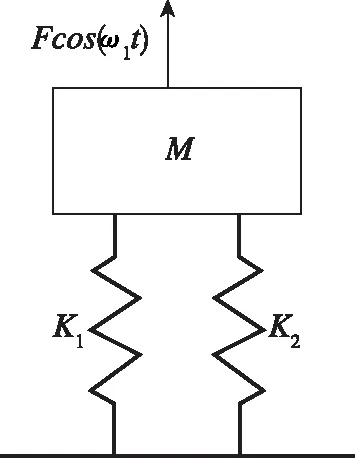
(a)单自由度模型[22]

(b)2自由度模型[23]图2 螺栓连接部CAN的理论模型Fig.2 Theoretical modeling of CAN in bolt joint
1.2 数值建模
仅利用上述简化的理论分析模型不能准确全面理解导波与螺栓连接部的相互作用机理。由于螺栓结构在波传播方向是不均匀的,因此不能用解析或半解析方法模拟波在螺栓连接结构中的传播。有限元法(FEM)可应用于各种复杂的几何形状,已成为应用最广泛的波传播分析方法。因此,Clayton等[24]建立了螺栓连接结构中导波传播的三维有限元模型,但为了降低计算成本,其未考虑界面接触。然后Doyle等[25]、Bao等[26]使用相同的方法建立有限元模型。然而,他们发现这些模型不能反映不同螺栓预紧力下导波信号的变化。为了考虑界面接触,Bao等[27]在有限元模型中增加了接触单元,改进后的模型能够反映不同预紧力下导波信号的变化,然而信号变化幅度和测量结果有较大差异。上述模型中接触面均为光滑的,但实际的接触表面是粗糙表面。2016年,Parvasi等[14]试图通过随机调整接触表面处的节点位置以在有限元模型考虑粗糙表面接触,如图3所示,其模拟结果更接近实验测量结果,但接触面上的网格尺寸(1.8mm)比粗糙表面上的微粗糙体的尺寸大得多。
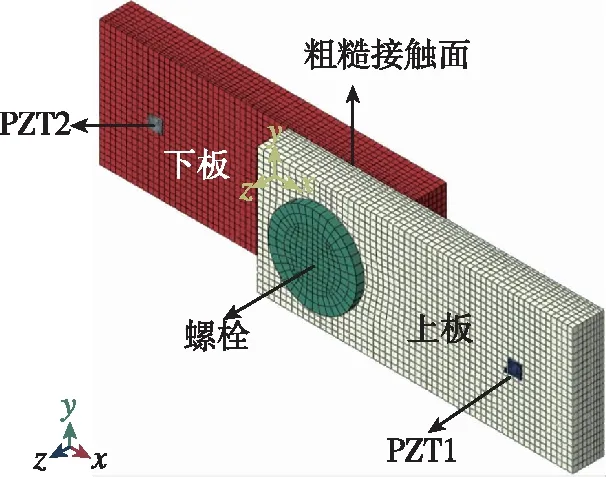
图3 考虑PZT传感器的螺栓搭接结构有限元模型[14]Fig.3 Model geometry (meshed structure): two steel plates joined by a nut and bolt connection with the surface of two PZT transducers mounted on the two plates[14]
上述有限元模型主要用于分析螺栓预紧力与透射导波能量之间的关系。 Shen等[28]建立了考虑接触的三维有限元模型来分析由接触非线性导致的二次谐波与螺栓预紧力之间的关系,如图4(a)所示。利用上述模型可以在透射导波信号的频谱中清晰地观察到非线性高次谐波(2阶谐波和3阶谐波),如图4(b)所示。仿真结果同时表明,随着螺栓预紧力的增加,二次谐波的幅值与激励频率幅值的比值随之减小。
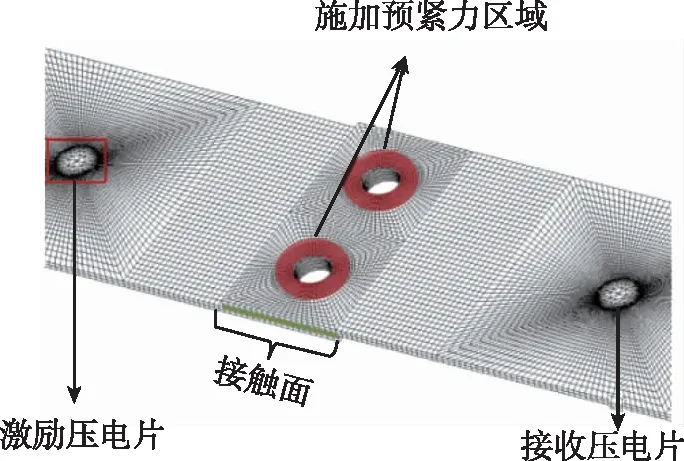
(a)有限元模型

(b)仿真结果图4 螺栓搭接结构的有限元模型及透射导波信号的频谱[28]Fig.4 Transient dynamic contact finite element model and frequency spectrum of simulation signal[28]
2 基于线性特征的监测方法
2.1 波能耗散方法
由于透过螺栓连接界面的超声导波能量与结合面的接触状态密切相关,因此直接利用透射导波能量作为检测指标的相关方法被广泛研究,这类方法也被称为导波能量耗散方法(Wave Energy Dissipation, WED)。针对航天飞机机翼前缘热防护板中的螺栓预紧力监测问题,Yang等[4,29]利用穿过螺栓连接界面的导波能量以及导波能量衰减速度来估计螺栓扭矩水平和松动螺栓的位置。随后,Wang等[30]使用相似的WED方法来监测螺栓预紧力,实验设置如图5所示。实验结果如图6(a)所示,可以看出导波透射能量基本上与扭矩水平成正比,但是当施加的转矩达到一定值时,能量不会随着螺栓扭矩而变化,这就是所谓的饱和现象。同样,Amerini等[31]在信号频域中计算了透射导波的能量,用以评估螺栓搭接接头的紧固状态,实验结果如图6(b)所示,仍然可以看到较为明显的饱和现象。Yang等[32]将WED方法扩展到复合材料螺栓连接预紧力监测。 Haynes等[33]利用激光测振仪,对导波在螺栓搭接结构中的传播进行了全场测量,通过计算螺栓搭接部前后的导波能量监测螺栓扭矩水平,但其实验结果中也观察到饱和现象。另一方面,由于导波的多模态、频散和边界反射,螺栓连接处的导波响应信号相当复杂[31]。因此,Kędra等[34]研究了激励频率,接收导波信号时间窗口,传感器位置等对WED方法检测精度的影响,其结果表明这些参数必须慎重选择才能获得较好的测量精度。

图5 螺栓连接监测系统示意图[30]Fig.5 Schematic of the bolt connection monitoring system[30]
上述螺栓预紧力监测方法仅限于含单螺栓的平面螺栓搭接结构,然而在实际结构中,含有复杂零件或多个螺栓的连接结构更为常见,此时,一般需要较为复杂的信号处理方法。 Jalalpour等[35]为了监测L形螺栓连接预紧力,提出了一种利用快速Fourier变换,互相关和模糊模式识别来处理导波信号的预紧力监测方法,该方法实现了预紧扭矩的准确检测,然而其扭矩水平的模糊集合是有限的,限制了其检测分辨率。Montoya等[36]使用透射导波能量评估了L形螺栓连接结构的刚度。随后,Montoya等[37]进一步将该方法扩展到连接卫星面板的直角支架中螺栓预应力监测。实验结果显示,一些测量参数,如接收导波信号的时间窗口等,对测量的灵敏度和可重复性有重要影响。Mita等[38]针对多螺栓连接结构的螺栓松动监测,提出使用支持向量机来识别不同的松动模式。结果表明,该方法可以识别松动螺栓的位置和松动程度。此后,Liang等[39]为多螺栓结构开发了一种决策融合系统,如图7所示。该系统由个体分类、分类器选择和决策融合组成。实验结果表明,所提出的方法能够通过分析获取的导波信号准确快速地识别松动螺栓及其位置。

(a)文献[30]结果

(b)文献[31]结果图6 WED方法的检测结果Fig.6 Results of WED methods
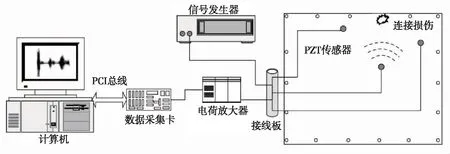
图7 松动螺栓位置及传感器布置[39]Fig.7 Sensor layout and joint failure position on the specimen[39]
2.2 时间反转方法
由于导波的多模态、频散及散射特性,导波信号总是非常复杂,为此Ing等[40]将时间反转法(Time Reversal, TR)扩展到导波检测技术中。在时间反转方法中,接收到的信号被时域反转并作为激励信号重新发射,然后可以在原发射位置重构输入信号。因此,时间反转方法可以有效地减小导波的频散、多模态等的影响。近年来,基于时间反转的导波监测方法已广泛应用于金属[41]、复合材料[42-44]和钢筋混凝土梁[45]等的损伤检测中。因此王强等[46]、Parvasi等[14]分别提出采用时间反转法对通过螺栓连接部的导波信号进行聚焦,然后利用聚焦信号的峰值作为预紧力检测的拧紧指标,实验结果表明,所提出的拧紧指数随着螺栓扭矩而增加。螺栓预紧力的TR监测方法可以分为以下4个步骤,如图8所示。
步骤1:将一个窄频脉冲信号e(t)施加到压电激励器A,该压电传感器在搭接板中激励出超声导波;
步骤2:由压电传感器B接收导波响应信号u(t);
步骤3:将接收到的信号u(t)在时域上反转并且使用压电传感器B重新激励;
步骤4:通过压电传感器A再次接收导波信号,这样原始的输入信号可以被重建,然后重建信号的峰值可以被用作预紧力检测[14]。
上述信号峰值直接反应了透射导波的能量,不需要像WED方法一样为接收信号时间窗口的选择花费努力。
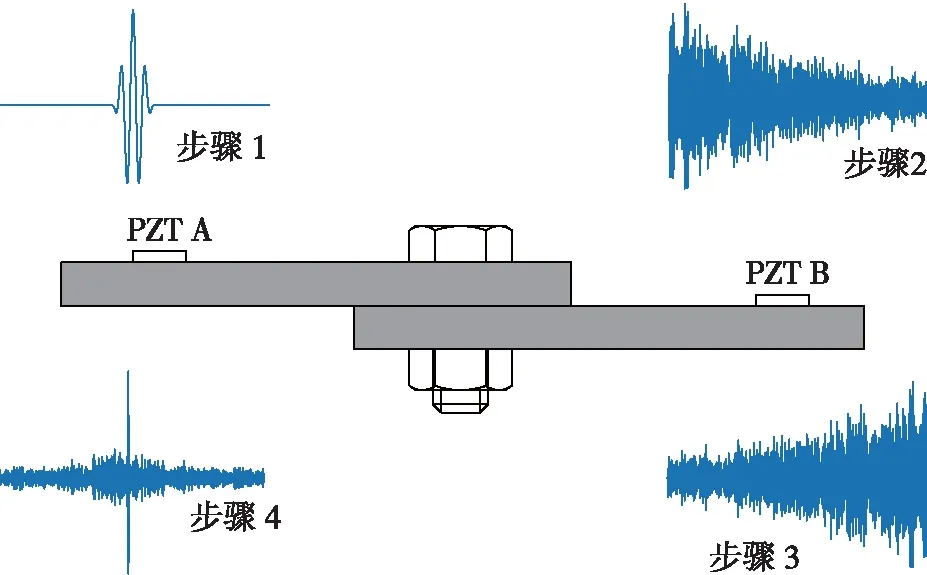
图8 螺栓预紧力的时间反转导波检测示意图Fig.8 Illustration of the time reversal method in a lap jointed beam
由于重新聚焦信号反映了透射波的能量,因此当螺栓预紧力相对较高时,同波能耗散法类似,聚焦信号峰值振幅变化非常缓慢。王涛等[47-48]实验研究了螺栓预紧力检测的时间反转导波法,结果证明随着螺栓连接界面表面粗糙度的增加,饱和现象变得不明显。Huo等[49]基于分形接触理论和有限元方法研究了螺栓连接界面上导波的时间反转过程,其分析结果表明,时反检测中饱和现象与重载荷下接触微凸体的塑性变形有关。
2.3 时间反转法与波能耗散法的对比
本节通过实验对比了WED和TR方法的监测精度,所采用的实验装置和试样如图9所示。被测的试件为铝合金螺栓搭接结构,铝的材料为2024-T3,每根铝板的长度为400mm,宽度为50mm,厚度为2mm。两根铝板用M6螺栓连接。实验中选择10N·m预紧力为正常扭矩,并采用分辨率为0.2N·m的扭矩扳手施加螺栓预紧力。实验时,将试件放在泡沫支撑上以模拟自由边界条件。两个PZT贴片黏在螺栓搭接部两侧,与螺栓间的距离均为100mm,其编号分别为PZT 1、PZT 2。实验中利用NI USB-6366数据采集(DAQ)系统生成波形激励并记录压电传感器的相应,其每个通道采样频率为2MHz。在LabVIEW环境中编制了一个数据采集程序来进行信号激励及数据采集。高压放大器PINTEK HA-400用于放大激励信号并向PZT传感器提供电压。

图9 实验装置和试件Fig.9 Experimental setup and specimens
实验中同时采用WED和TR方法检测螺栓预紧力,在WED方法中,在接收信号中选取特定的长度计算其能量作为拧紧指数TI_Ω(WED),结果如图10(a)所示。 从图中可以看出,在扭矩为6N·m前拧紧指数基本随着扭矩的增加而增加,但是在2N·m~6N·m时,其变化并不明显,同时可以看到一个明显的饱和现象,只有最小的0.1N·m扭矩情况可以被非常清晰地识别。在TR方法中,利用重聚焦信号的峰值作为拧紧指数TI_Ω(TR),结果如图10(b)所示。 从图中可以看出,在全部检测范围内,拧紧指数随着预紧力的增加而增加,但是在6N·m~10N·m之间,其变化并不明显,而在6N·m之前可以明确地识别出各个扭矩,这表明采用TI_Ω(TR)时其的灵敏度高于TI_Ω(WED),特别是在螺栓松动的早期阶段。其主要原因是,采用TR方法时,导波通过连接界面了两次(从PZT1到PZT2,然后是PZT2到PZT1),界面特性会两次影响波的传播,从而使TI_Ω(TR)对螺栓预紧力更敏感[14]。
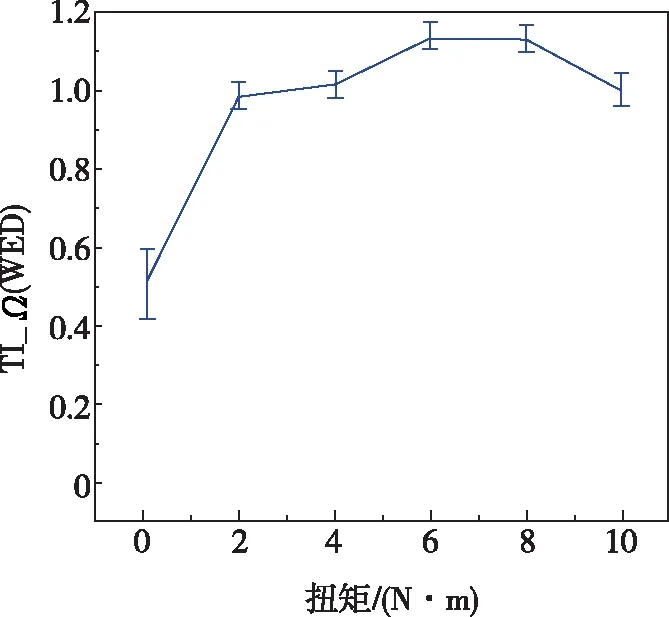
(a)TI_Ω(WED)指标随着扭矩的变化
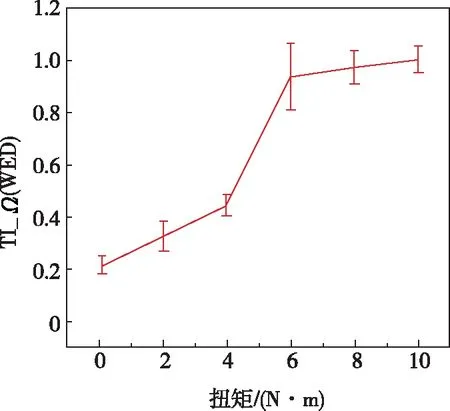
(b)TI_Ω(TR)指标随着扭矩的变化图10 WED和TR方法的检测结果Fig.10 Results of the WED based approach and the TR method
3 基于非线性特征的监测技术
3.1 接触声学非线性(CAN)
由于连接界面的存在,随着预紧力的降低,接触声学非线性(CAN)会随之增加,所以目前学者已经将由CAN引起的二次谐波、次谐波和边频带用于螺栓预紧力检测。通常二次谐波和次谐波由单个频频率激励产生,此时可以利用二次谐波或次谐波的幅值与激励频率的幅值之间的比值,作为评估螺栓预紧力拧紧指标。而边频带则同时需要低频和高频信号激励产生,此时其拧紧指数一般利用两个边频带幅值的平均值与高频激励频率的幅值之间的差值作为拧紧指标[31]。Zhang等[23]提出了螺栓连接结构次谐波的激励方法,并在此基础上提出了螺栓松动检测方法。Amerini等[31]分别建立了2阶谐波指数和边频带指数来评估螺栓结构的拧紧状态。随后,Zhang等[21-22]提出了基于振动声学调制(VAM)的方法,并利用基于边频带的拧紧指数对为金属和复合材料螺栓连接结构进行了预紧力检测,图11(a)为复合材料螺栓连接预紧力的实验装置,以及相应的检测结果。

(a)实验装置
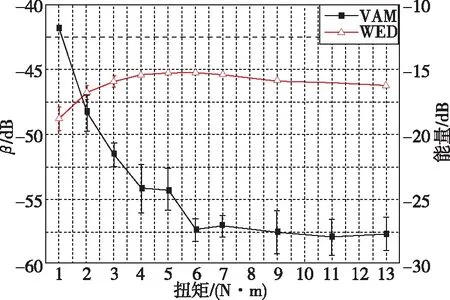
(b)VAM与WED结果对比[21]图11 基于VAM的复合材料螺栓连接预紧力监测Fig.11 Preload monitoring of bolted composite joint using VAM method
将其检测结果与WED方法进行了对比,如图11(b)所示,比较结果表明其所采用的非线性方法的测量灵敏度高于WED方法,特别是在松动初期,此时WED方法由于饱和现象无法实现松动检测,但是图中结果也显示非线性方法存在一定的饱和现象。随后,Zhang等[20]将基于高次谐波和边频带的螺栓预紧力检测方法进行了对比,证明了基于边频带的检测方法稳定性较好。另一方面,边频带也可以通过冲击调制产生,Meyer等[50]提出了一种基于冲击调制的方法来检测铝螺栓连接部中的螺栓松动。然而利用该方法时,边频带幅值对于测试参数(包括冲击激励的振幅和位置),检测传感器的位置等都较为敏感。基于边频带方法的另外一个的缺点是,它需要两个不同类型的激励器和传感器来监测单个螺栓的预紧力[31]。
3.2 相位变化
除了导波透射能量、CAN之外,透射导波的相移变化也用于螺栓预紧力检测。Zagrai等[51]提出通过测量穿过螺栓连接处的导波相位延迟来估计螺栓扭矩,其实验结果表明,螺栓扭矩与导波信号的相移成正比,如图12所示。

(a)信号整体
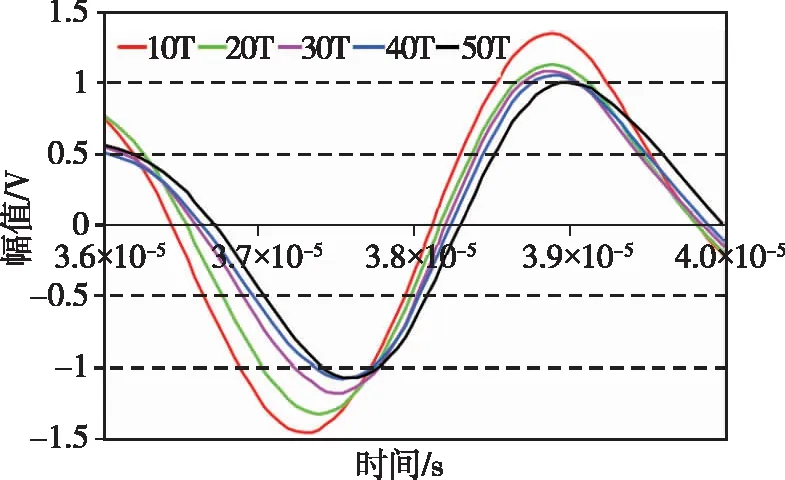
(b)局部放大图12 不同扭矩下的导波信号Fig.12 Guided wave signals recorded at different bolt torques
Zagrai等[51]试图用声弹理论来解释上述实验结果,并提出了一种简化的理论方法来计算通过螺栓连接处导波的相移,然而其理论结果与实验结果相比低了一个数量级。随后,Doyle等[52-53]进一步利用稀疏分布的压电传感器阵列对包含49个螺栓的典型卫星面板进行了检测,结果表明,导波相位变化发生的时间与松动螺栓的位置和导波主传播路径之间的距离有关。因此,仅使用2条或3条导波传播路径就可以实现松动螺纹及其位置的检测[53]。在此基础上,Zagrai等[54]试图采用具有不同初始相位的导波信号来实现螺栓松动的无参考信号检测。但该方法不适用于具有复杂几何形状和大量螺栓的结构。然而由螺栓连接引起的导波相移变化相当小,需要采用具有高采样频率的数据采集设备[52],同时由于接收到的导波信号非常复杂,因此很难选择正确的时间窗和相应的波速来计算相移和导波路径与松动螺栓间的距离。
3.3 混沌超声激励
除了利用上述接触声学非线性、声弹等螺栓连接部的非线性特征外,另一个研究思路是直接使用非线性超声激励,此时通过在超声波激励信号中人为引入非线性分量可以灵敏地检测到螺栓松动导致的结构参数改变,也能有效克服由于压电元件的激励幅值较小,很难激起结构本身的非线性的缺点。为此,Clayton等[24]提出了一种将混沌激励和超声导波相结合的螺栓预紧力监测方法。该方法通过对混沌振动信号进行升频调制,生成具有混沌特性的超声信号激励待测结构,对响应信号进行重构相空间分析,提取表征螺栓松动的非线性特征量。虽然大多数著名的混沌系统产生的混沌信号不适合用于激励导波,但通过升频调制,混沌信号从低频变为超声频带,而超声频率较高对小量级损伤较为敏感。 Fasel等[55-56]使用了类似的方法在单螺栓和多螺栓结构中识别螺栓预紧力变化。最近,吴冠南等[57]将用于表征吸引子的整体特征和局部特征的Lyapunov维数和平均吸引子局部方差比ALAVR都作为螺栓拧紧指数,以识别螺栓预紧力。实验对比结果表明,ALAVR更适合螺栓预载荷监测,对比结果如图13所示。
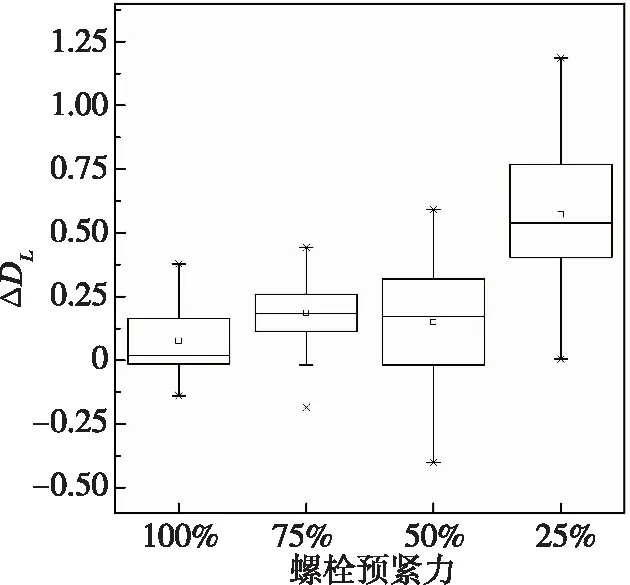
(a)Lyapunov维数
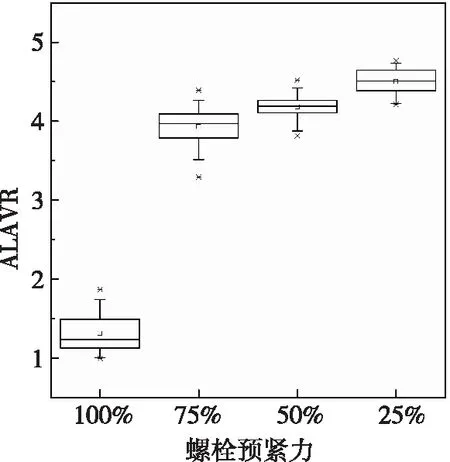
(b)ALAVR图13 不同螺栓预紧力工况下的特征量[57]Fig.13 Tightness indexes VS bolt preload[57]
4 结论
超声导波是螺栓预紧力监测的有效方法,本文对该领域的研究现状进行了综述。目前该领域已经取得了相当大的进展。由螺栓连接部引入到导波信号的线性和非线性特征均已用于螺栓预紧力监测。其中,透射导波能量作为线性特征目前最为广泛地用于单螺栓和多螺栓结构中的预紧力监测。为此本文将利用上述特征进行检测的波能耗散法(WED)与时间反转法(TR)进行了实验对比,结果表明TR方法比螺栓松动方法对螺栓松动更敏感。同时本文也回顾了多种基于非线性特征的检测方法,包括接触声学非线性、声弹导致的相移以及混沌超声检测,上述方法可以在一定程度上提高检测灵敏度,但是也存在不同的缺点,比如更高频的采样频率,或者同时需要声学和振动激励。今后亟待解决的问题如下:
1)应进一步发展准确高效的分析方法,以精确模拟螺栓连接部中导波的传播。例如,目前认为声弹导致了透射导波信号相位的变化,而目前简化的理论模型并不能解释信号相位变化,同时现在有限元模型中很难考虑连接接触面上的表面形貌。因此,建立更精准高效的数值模型有望更准确地解释连接界面和导波之间的相互作用,解释上述实验现象。
2)仍需要改进螺栓预紧力导波监测方法。虽然目前时间反转法和振动声调制等方法可以有效提高螺栓预紧力的检测灵敏度,但在螺栓松动的早期阶段,这些方法的检测灵敏度并不是很好。 另一方面,目前几乎所有的方法都需要从健康结构中获取参考信号。因此,如何建立检测灵敏度较高的无参考信号方法,是实现导波螺栓预紧力监测工程应用的重要步骤。
3)应进一步发展多螺栓连接结构中预紧力导波监测方法。现有文献中的研究仅限于含单螺栓的搭接平板结构,而对于多螺栓或者复杂结构关注较少,缺乏多螺栓等结构的预紧力监测方法,然而这些结构在工程中更为常见。
4)进一步发展复杂多物理场耦合条件的预紧力监测方法和验证。现有文献中的研究大多未考虑温度、电磁等复杂多物理场环境的影响,技术验证多在实验室条件下进行。为进一步推动该技术的工程应用,应着力发展多物理场和服役环境条件下的预紧力监测,并在飞行器型号上进行前沿技术验证研究。

